Proportions

Rescuing Jack and Rose

Abstract

Single and Nested Proportions with Qual Variables

What graphs will we see today?

Variable #1	Variable #2	Chart Names	Chart Shape
Qual	Qual	Pies, and Mosaic Charts

What kind of Data Variables will we choose?

No	Pronoun	Answer	Variable/Scale	Example	What Operations?
3	How, What Kind, What Sort	A Manner / Method, Type or Attribute from a list, with list items in some " order" ( e.g. good, better, improved, best..)	Qualitative/Ordinal	Socioeconomic status (Low income, Middle income, High income),Education level (HighSchool, BS, MS, PhD),Satisfaction rating(Very much Dislike, Dislike, Neutral, Like, Very Much Like)	Median,Percentile

Inspiration

(a) Obesity across the World

(b) Covid Deaths https://datatopics.worldbank.org/sdgatlas/goal-3-good-health-and-well-being?lang=en

Figure 1: Depicting Proportions

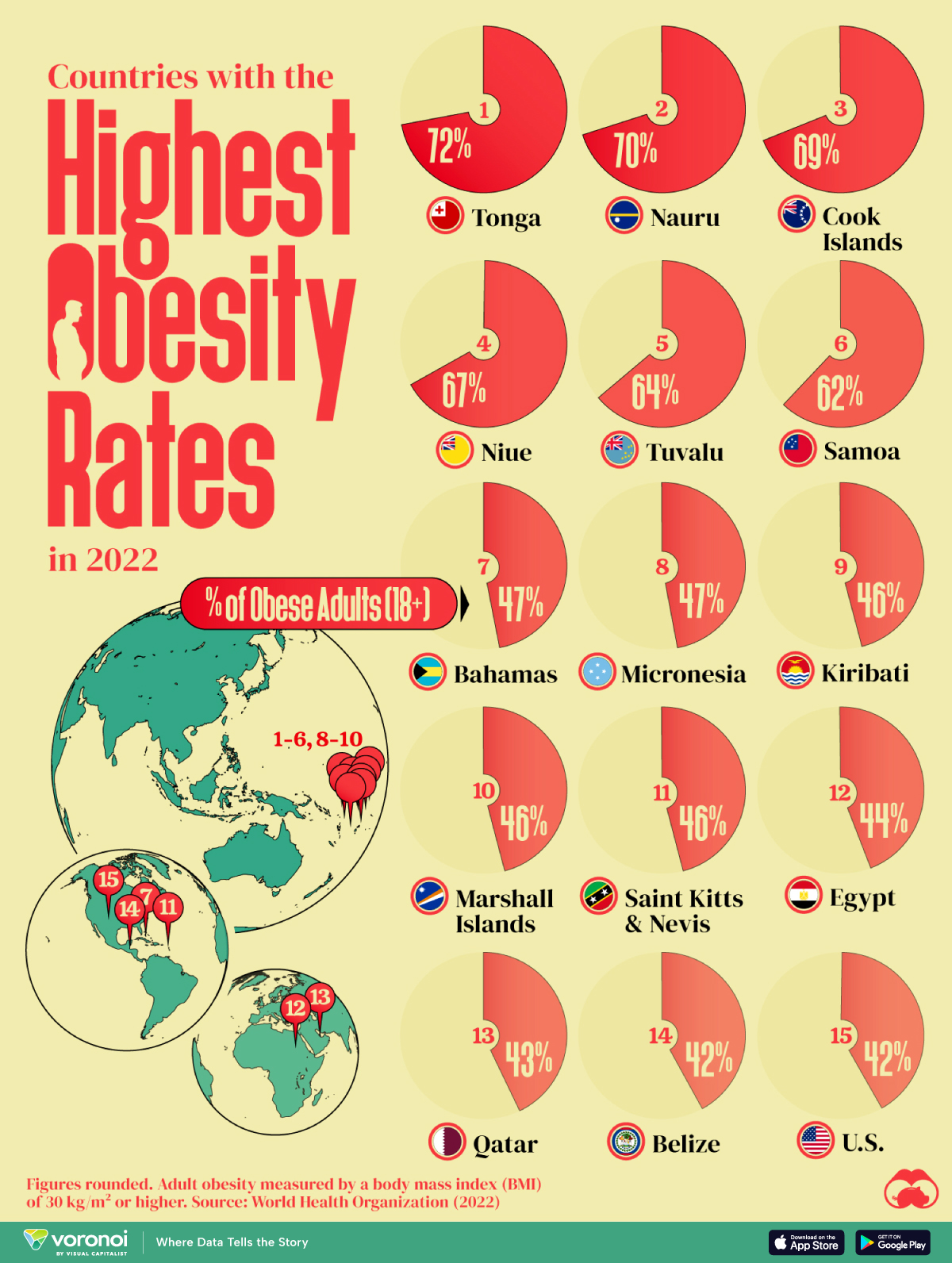
From Figure 1 (a), it is seen that Egypt, Qatar, and the United States are the only countries with a population greater than 1 million on this list. Poor food habits are once again a factor, with some cultural differences. In Egypt, high food inflation has pushed residents to low-cost high-calorie meals. To combat food insecurity, the government subsidizes bread, wheat flour, sugar and cooking oil, many of which are the ingredients linked to weight gain. In Qatar, a country with one of the highest per capita GDPs in the world, a genetic predisposition towards obesity and sedentary lifestyles worsen the impact of rich diets. And in the U.S., bigger portions are one of the many reasons cited for rampant adult and child obesity. For example, Americans ate 20% more calories in the year 2000 than they did in 1983. They consume 195 lbs of meat annually compared to 138 lbs in 1953. And their grain intake has increased 45% since 1970.

It’s worth noting however that this dataset is based on BMI values, which do not fully account for body types with larger bone and muscle mass.

From Figure 1 (b), according to World Bank, six countries (India, Russia, Indonesia, United States, Brazil, and Mexico) accounted for over 60 percent of the total additional deaths in the first two years of the pandemic.

How do these Chart(s) Work?

We saw with Bar Charts that when we deal with single Qual variables, we perform counts for each level of the variable. For a single Qual variable, even with multiple levels ( e.g. Education Status: High school, College, Post-Graduate, PhD), we can count the observations as with Bar Charts and plot Pies.

What if there are two Quals? Or even more?

The answer is to take them pair-wise, make all combinations of levels for both and calculate counts for these. This is called a Contingency Table. Then we plot that table. We’ll see.

Plotting Pies

Let us deal with single Qual variables first.

Using Orange

Let us the same dataset as is used in the RAWgraphs tutorial (to follow):

Can you find the Pie Chart Widget in Orange? Let us do this “live” in class and test our new-found Orange skills!

Using RAWgraphs

Download this RAWgraphs project workflow and open it in RAWgraphs.

Note

Note the shape of data here: it is wide!

Using DataWrapper

https://academy.datawrapper.de/article/24-how-to-create-a-pie-chart

The problem is that humans are pretty bad at reading angles. This ubiquitous chart is much vilified in the industry and bar charts that we have seen earlier, are viewed as better options. On the other hand, pie charts are ubiquitous in design and business circles, and are very much accepted! Do also read this spirited defense of pie charts here. https://speakingppt.com/why-tufte-is-flat-out-wrong-about-pie-charts/

Plotting Nested Proportions

When we want to visualize proportions based on Multiple Qual variables, we are looking at what Claus Wilke calls nested proportions: groups within groups. Making counts with combinations of levels for two Qual variables gives us a data structure called a Contingency Table, which we will use to build our plot for nested proportions

What is a Contingency Table?

From Wolfram Alpha:

A contingency table, sometimes called a two-way frequency table, is a tabular mechanism with at least two rows and two columns used in statistics to present categorical data in terms of frequency counts.

More precisely, an \(r \times c\) contingency table shows the observed frequency of two variables the observed frequencies of which are arranged into \(r\) rows and \(c\) columns. The intersection of a row and a column of a contingency table is called a cell.

The Contingency Table is then plotted in a chart called the Mosaic Chart. Let us develop our intuition for a Contingency Table first, and arrive at the mosaic chart.

Dataset: General Social Survey 2002

Let us first construct a Contingency Table from this dataset, and then plot the mosaic chart for it.

Here is the Orange workflow:

Examine the Data

Figure 2: GSS2002 Data Table

(a) GSS2002 Data Summary #1

(b) GSS2002 Data Summary #2

Figure 3: General Social Survey 2002 Dataset

Data Dictionary

Quantitative Data

• ID is the only Quant data variable!

Qualitative Data

“ID” “Region” “Gender” “Race”
“Education” “Marital” “Religion” “Happy”
“Income” “PolParty” “Politics” “Marijuana”
“DeathPenalty” “OwnGun” “GunLaw” “SpendMilitary” “SpendEduc” “SpendEnv” “SpendSci” “Pres00”
“Postlife”

are all Qual variables! Let us choose just two Qual variables from this dataset, DeathPenalty and Education.

• DeathPenalty: (chr) Opinion as to whether they favour or oppose the death penalty
• Education: (chr) Education among respondents, 5 levels (Left HS, HS, Jr Col, Bachelors, Graduate).

A Contingency table with these two Qual variables looks like Figure 4:

DeathPenalty	Left HS	HS	Jr Col	Bachelors	Graduate	Sum
Favor	117	511	71	135	64	898
Oppose	72	200	16	71	50	409
Sum	189	711	87	206	114	1307

Figure 4: Contingency Table

How was this computed?

So \(117\) is the number of people who Left HS and Favor the death penalty, and \(71\) is the count for Bachelors who Oppose the death penalty. And so on.

Now then, how does one plot a set of data that looks like this, a matrix? No column is a single variable, nor is each row a single observation, which is what we understand with the idea of tidy data.

The answer is provided in the very shape of the data: we plot this as a set of tiles, where \[ \pmb{area~of~tile \sim count} \] In this way we recursively partition off a (usually) square area into vertical and horizontal pieces whose area is proportional to the count at a specific combination of levels of the two Qual variables. So we might follow the process as shown below:

• Take the bottom row of per-column totals and create vertical rectangles with these widths
  
• Take the individual counts in the rows and partition each rectangle based in the counts in these rows. 

Let us do this step by step.

Research Questions

Question

Q1. Are Education and DeathPenalty associated?

Let us plot the mosaic chart in two steps: we now choose Qual variables Education and DeathPenalty, in that order to plot the mosaic chart. Here are the two steps in the recursion:

(a) GSS Mosaic Chart Step #1

(b) GSS Mosaic Chart Step #2

Figure 5: Mosaic Chart for GSS Data

The first split shows the various levels of Education and their counts as widths. Order is alphabetical! This splitting corresponds to the bottom ROW of the Figure 4. HS is clearly the largest subgroup in Education.

In the second step, the columns from Figure 5 (a) are sliced horizontally into tiles, in proportion to the number of people in each Education category/level who support/do not support DeathPenalty. This is done in proportion to all the entries in each COLUMN.

Important

Note that the order in which we choose the variables matters, since the mosaic plot is fundamentally asymmetric. More on this in a bit.

Colouring by Pearson Residuals

Mosaic Charts generated by Orange can be coloured based on “Pearson Residuals”. What this means is that the mosaic plot calculates what might be the “expected counts” (see below) in the Contingency Table and calculates the differences (i.e. “residuals” ) between Observed/Actual and Expected values. If the errors are negative (Obs < Exp) then the tile is coloured red. And blue if the error is positive (Obs > Exp).

In Figure 5 (b) we see that there is a small positive and a small negative residual at two locations in the mosaic chart. By and large the chart is white, showing very little association between Education and DeathPenalty. However, we should verify this using a statistical “chi-square” \(X^2\) test.

More on “expected counts” and the “chi-square” \(X^2\) test below.

Plotting Mosaic Charts

Using Orange

The description of the Orange widget for mosaic charts is here.

Let us take a very sadly famous data set (no, not iris again 🙀), but titanic and examine it in Orange.

We will reuse this workflow:

Using RAWgraphs

Not a mosaic plot, but a Matrix Plot.

Download this RAWGraphs workflow file and import there and see.

Using DataWrapper

Does not seem to have a mosaic diagram capability.

Dataset: Titanic

Ok, let us see if we can rescue Jack also. Here is the titanic data. Use the Datasets widget in Orange to get it.

Examine the Data

(a) Titanic Data Table

(b) Titanic Data Summary Stats

Figure 6: Titanic Data

There were 2201 passengers, as per this dataset.

Data Dictionary

Quantitative Data

None.

Qualitative Data

• survived: (chr) yes or no
• status: (chr) Class of Travel, else “crew”
• age: (chr) Adult, Child
• sex: (chr) Male / Female.

Research Questions

Q.1. What is the dependence of survived upon sex?

Figure 7: Titanic Mosaic Chart #1

Note the huge imbalance in survived with sex: men have clearly perished in larger numbers than women. Which is why the colouring by the Pearson Residuals show large positive residuals for men who died, and large negative residuals for women who died.

So sadly Jack is far more likely to have died than Rose.

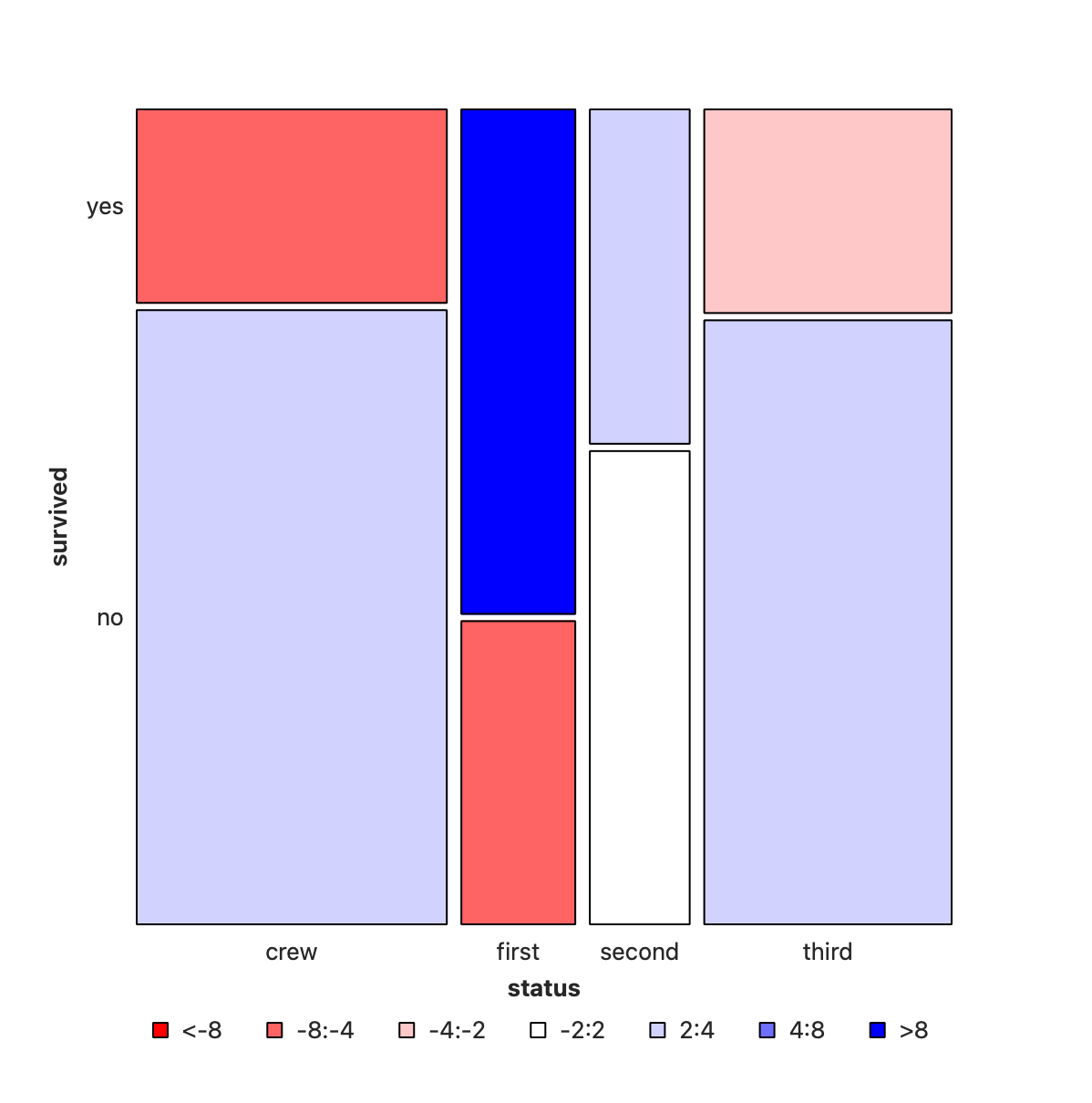
Q.2. How does survived depend upon status?

Figure 8: Titanic Mosaic Chart #2

Crew has seen deaths in large numbers, as seen by the large negative residual for crew-survivals. First Class passengers have had speedy access to the boats and have survived in larger proportions than say second or third class. There is a large positive residual for first-class survivals.

Rose travelled first class and Jack was third class. So again the odds are stacked against him.

What is the Story Here?

In Figure 8, we have plotted survived vs status. As can be seen the areas are very dissimilar across both variables. More deaths occurred among the crew than among the passengers; and more first class passengers have survived than third class passengers. And from Figure 7, more men died than women.

So we can state that:

• Status and Survived are not un-associated
• Sex and Survived are not un-associated
• Does ticking the Compare with Total box in Orange help to arrive at this inference? How so? Or does it confuse?

Are these differences in proportion significant?

It remains to figure out just how serious this association is, or whether these differences in proportion just happenned by chance. For that we need the statistical “chi-square” \(X^2\) test.

Actual and “Expected” Counts

The mosaic chart is a visualization of the obtained counts, based on which the tiles are constructed.

It is also possible to compute a per-cell expected count, if the categorical variables are assumed independent, that is, not correlated. This is the NULL Hypothesis. The test for whether they are independent or not, as any inferential test, is based on comparing the observed counts with these expected counts under the null hypothesis. So, what might the expected frequency of a cell be in cross-tabulation table for cell \(i,j\) given no relationship between the variables of interest?

Represent the sum of row \(i\) with \(n_{+i}\), the sum of column \(j\) with \(n_{j+}\), and the grand total of all the observations with \(n\). And independence of variables means that their joint probability is the product of their probabilities. Therefore, the Expected Cell Frequency/Count is given by:

\[ \begin{array}{lcl} ~Expected~Count~ e_{i,j} &=& \frac{rowSum ~\times~colSum}{n}\\ &=& \frac{(n_{+i})(n_{j+})}{n}\\ \end{array} \]

The comparison of what occurred to what is expected is based on their difference, scaled by the square root of the expected, the Pearson Residual:

\[ \begin{array}{lcl} r_{i,j} &=& \frac{(Actual - Expected)}{\sqrt{\displaystyle Expected}}\\ &=& \frac{(o_{i,j}- e_{i,j})}{\sqrt{\displaystyle e_{i,j}}} \end{array} \]

The sum of all the squared Pearson residuals is the chi-square statistic, χ2, upon which the inferential analysis follows.

χ2-Test for the Cat-egorically Curious

For the intrepid and insatiably curious, there is an intuitive explanation, and some hand-calculations and walk-through of the Contingency table and the χ2-test here.

Dataset: Who Does the Housework?

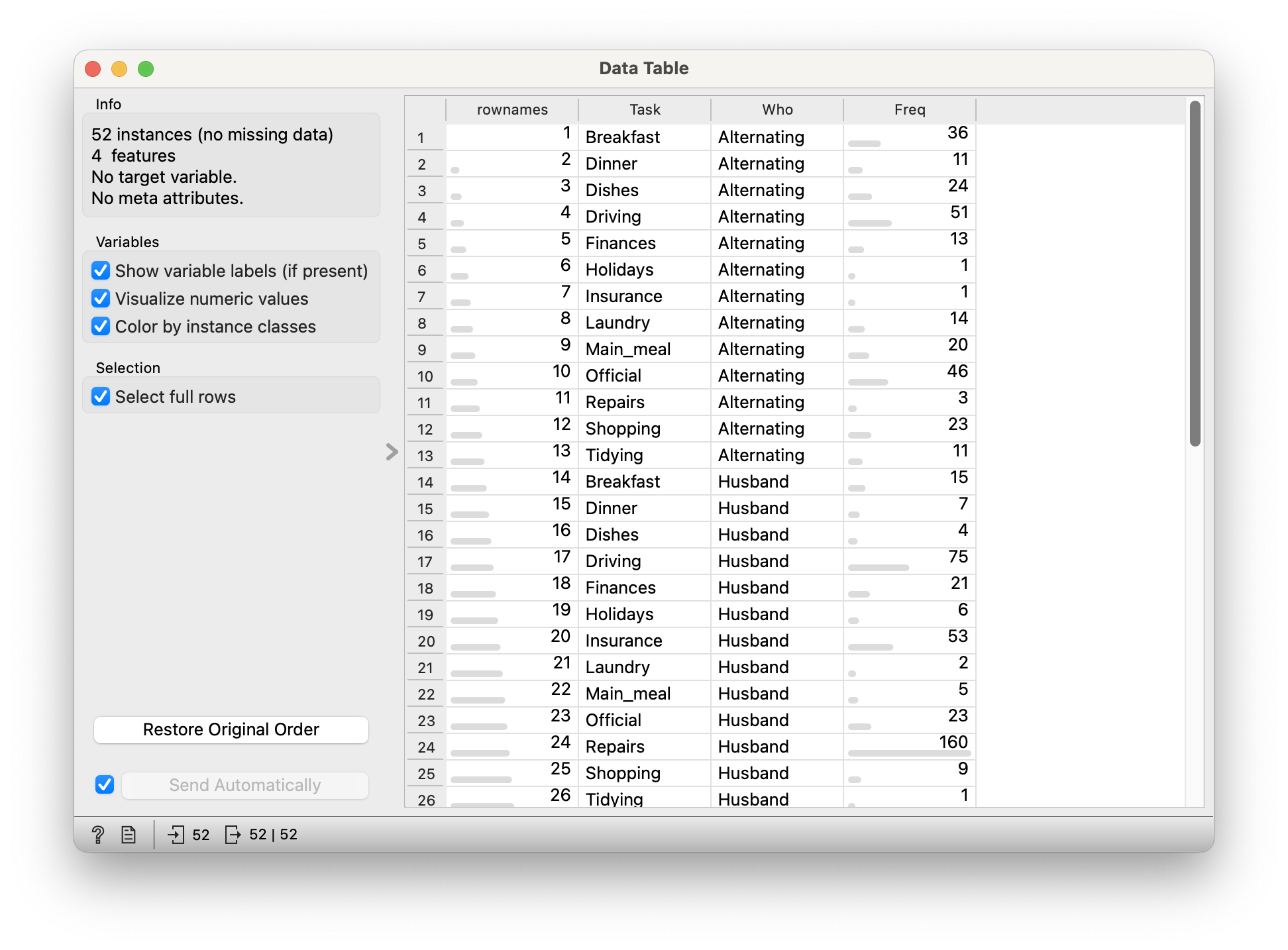
Let us take this dataset on household tasks, and who does them. Download this dataset and import in into your Mosaic Chart workflow.

Examine the Data

Figure 9: Household Tasks Distribution Raw Data

52 observations.

Data Dictionary

Quantitative Data

• Freq: (int) No of times a task was carried out by specific people

Qualitative Data

• Who: (chr) Who carried out the task?
• Task: (chr) Task? Which task? Can’t you see I’m tired?

Let us plot the mosaic chart:

Figure 10: Household Tasks Distribution Raw Data

This data looks fine all right, but this mosaic plot looks bewildering, utterly dumbfounding, and is of course wrong. The reason for this is that the basic HouseTasks.csv data is pre-aggregated: we have a neat column of counts already in the Freq data. Each combination of Qual factors has exactly one count/row/observation, hence all tiles are the same size.

And why is this a problem? Orange expects data to be purely categorical for the Mosaic Chart and does it own counting internally. It is not able to sensibly use this Freq column. Orange simply counts categories here, which are of course utterly symmetric, unique, and of no use. Bah!

Stat Figures and Stats

Most, if not all, statistical graphs do some internal computation. For instance the bar chart performs counts vs Qual variables; a Histogram both bins the Quant variable, and counts for entries in each bin. This is a good thing, peasants, but it does mean that the data needs to be in specific format before using it for plots. Cultivate that.

So now what? We need to (wait for it):

• uncount the data 🙀 🙀 🙀
• How? Take each combination of Quals Who and Task
• Repeat (i.e. copy-paste) that combo line as many times as the value in Freq
• (optionally) Deleting the Freq column, or at least not using it further

All this is (to the best of my ability) not possible in any of these trifling tools that we are using here, and can be done in a jiffy in R or Python. Didn’t I tell you coding was far far far far simpler? Oh, these peasants.

So following this ashtavakra procedure of jumping to another tool and coming back here, good things can be somehow made to happen, and so here is the “un-aggregated” data for you:

Import this into Orange.

Research Questions

Q.1 Is there association between Who carries out the task, and the Task itself?

Figure 11: Household Tasks Mosaic

What is the Story Here?

The Mosaic plot in Figure 11 is seriously coloured, showing that there are Pearson Residuals/Errors in both directions (positive and negative). The χ2-value is large (not visible here, check in Orange) and the p-value is zero. This indicates that it is very very unlikely that this data happened by chance, assuming the two Qual variables are un-related. Hence, we are likely to conclude that our assumption that they are un-related can be rejected. (Note this complex wording here. We don’t say they are related.)

Why is this unsurprising? Men don’t do housework, it would seem.

In general, if you want to spot association, look for serious amounts of colour in the mosaic chart.

Your Turn

Clothing and Intelligence Rating of Children!!

Are well-dressed students actually smarter? Isn’t that the exact reverse with SMI faculty? Or …?

Pre-marital Sex and Divorce.

Are Emily and Greg More Employable Than Lakisha and Jamal?

Are first names a basis for racial discrimination, in the US?

This dataset was generated as part of a landmark research study done by Marianne Bertrand and Senthil Mullainathan. Read the description therein to really understand how you can prove causality with a well-crafted research experiment.

Wait, But Why?

• We can detect correlation between Quant variables using the scatter plots and regression lines
• And we can detect association between Qual variables using mosaics and sieves (which we did not see here, but is possible in Orange)
• Your project primary research data may be pure Qualitative too, as with a Questionnaire / Survey instrument.
• One such Qual variable therein will be your target variable
• You will need to justify whether the target variable is dependent upon the other Quals, and then to decide what to do about that.

Survey Data and Likert Plots

Often times, the primary research questionnaire is in the form of Questions whose answer is on a Likert Scale data, where several respondents rate a product, or a service, on a scale of Very much like, somewhat like, neutral, Dislike and Very much dislike, for example. The data are again categorical; but a Contingency Table / Mosaic Chart would be quite complex to behold and understand. A Likert Plot is what is constructed at such times. Here is a sample Likert Plot for a fictitious app called “QuickEZ”:

Yeah, this is possible in R and Python. But not in these barbarian tools that we are using. There are some websites that offer free apps for these plots too.

For more tutorial information, head off to Visualizing Survey Data (in R).

Readings

1. Michael friendly. A Brief History of the Mosaic Display. https://www.datavis.ca/papers/moshist.pdf

2. David Meyer, Achim Zeileis, Kurt Hornik. Visualizing Contingency Tables. Some very clear and simple pictures at https://statmath.wu.ac.at/projects/vcd/

3. Nice Chi-square interactive story at https://statisticalstories.xyz/chi-square

4. A different graph on Housework Inequality, but the same story! https://datatopics.worldbank.org/sdgatlas/goal-5-gender-equality?lang=en#c4

References

1. CATAAS: Cat as a service. https://cataas.com. Please bookmark this.

2. Yet another Shipwreck story.