EDA: Exploring Interactive Graphs for Data Distributions in R

Author

Arvind Venkatadri

Published

November 19, 2022

Modified

July 29, 2025

Abstract

How to ask Questions of your Data and answer with Stats, and interactive Bar charts and Histograms with the echarts4r package

Setup the Packages

# options(tibble.print_min = 4L, tibble.print_max = 4L,digits = 3)
library(tidyverse)
library(mosaic) # package for stats, simulations, and basic plots
library(mosaicData) # package containing datasets
library(ggformula) # package for professional looking plots, that use the formula interface from mosaic
library(skimr) # Summary statistics about variables in data frames
library(NHANES) # survey data collected by the US National Center for Health Statistics (NCHS)

library(echarts4r) # Interactive graphs using Javascript in R
library(plotly) # An older more established package for interactive graphs using Javascript in R

ggplot2::theme_set(new = theme_classic())

Introduction

We will query our dataset, developing insights and new questions as each Table or Bar/Histogram chart yields new information. This process of exploration is iterative, structured, and intuitive. Intermediate results may on occasion be messy or not very insightful!

We will consistently use the Project Mosaic ecosystem of packages in R (mosaic, mosaicData and ggformula).

Formula Interface

Note the standard method for all commands from the mosaic package:
goal( y ~ x | z, data = mydata, …) With ggformula, one can create any graph/chart using:
gf_geometry(y ~ x | z, data = mydata)
OR
mydata %>% gf_geometry( y ~ x | z)
The second method may be preferable, especially if you have done some data manipulation first! More later! ggformula supports many types of plots (using geometry), such as scatter, bar, histogram, density, boxplots, maps and many other statistical plots.

Interactive Graphs with echarts4r

We will also start using echarts4r side by side for interactive graphs.

Every function in the package starts with e_.
You start coding a visualization by creating an echarts object with the e_charts() function. That takes your data frame and x-axis column as arguments.
Next, you add a function for the type of chart (e_line(), e_bar(), etc.) with the y-axis series column name as an argument.
The rest is mostly customization! echarts4r takes some effort in getting used to, but it totally worth it!

The website for echarts4r is https://echarts4r.john-coene.com/articles/get_started.html. You should also quickly view this short introductory video on echarts4r:

Case Study-1: Galton Dataset from `mosaicData`

Let us choose the famous Galton dataset:

data("Galton")
Galton <- as_tibble(Galton)

Look at the Data:

skim(Galton)

Data summary
Name	Galton
Number of rows	898
Number of columns	6
_______________________
Column type frequency:
factor	2
numeric	4
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
family	0	1	FALSE	197	185: 15, 166: 11, 66: 11, 130: 10
sex	0	1	FALSE	2	M: 465, F: 433

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
father	1	69.23	2.47	62	68	69.0	71.0	78.5	▁▅▇▂▁
mother	1	64.08	2.31	58	63	64.0	65.5	70.5	▂▅▇▃▁
height	1	66.76	3.58	56	64	66.5	69.7	79.0	▁▇▇▅▁
nkids	1	6.14	2.69	1	4	6.0	8.0	15.0	▃▇▆▂▁

What can we say about the dataset and its variables? How big is the dataset? How many variables? What types are they, Quant or Qual? What are the means, medians and inter-quartile ranges for the Quant variables? If they are Qual, what are the levels? Are they ordered levels?

There is a lot of Description generated by the skimr::skim command (and equivalently by the mosaic::inspect() command)! Try both and see which output suits you. The first table above describes the Qual variables: family and sex. The second table describes the Quant variables, and gives us their statistical summaries as well and a neat little histogram to boot. The data are described as:

Type help(Galton) in your Console

A data frame with 898 observations on the following variables.

family an ID for each family, a factor with levels for each family

father the father’s height (in inches)

mother the mother’s height (in inches)

sex the child’s sex: F or M

height the child’s height as an adult (in inches)

nkids the number of adult children in the family, or, at least, the number whose heights Galton recorded.

Counts, and Charts with Counts

Now that we know the variables, let us look at counts of data observations(rows). We know from our examination of variable types that counting of observations must be done on the basis of Qualitative variables. So let us count and plot the counts in bar charts.

Question

Q.1 How many families in the data for each value of nkids(i.e. Count of families by size)?

Galton_counts <- Galton %>%
  group_by(nkids) %>%
  summarise(children = n()) %>%
  # just to check
  mutate(
    No_of_families = as.integer(children / nkids),
    # Why do we divide

    running_count_of_children = cumsum(children),
    running_count_of_families = cumsum(No_of_families)
  )
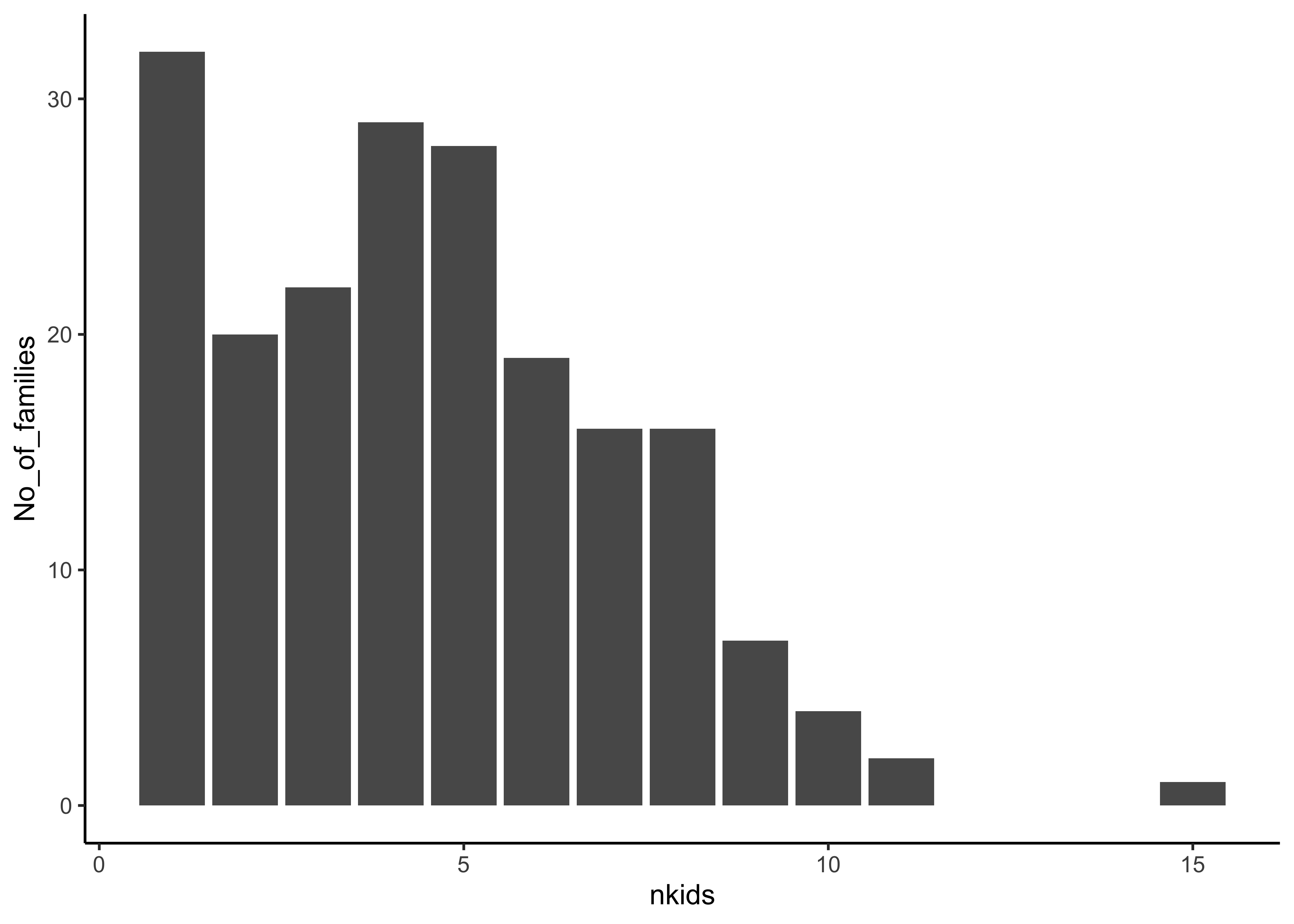
Galton_counts

ABCDEFGHIJ0123456789

nkids <int>	children <int>	No_of_families <int>	running_count_of_children <int>	running_count_of_families <int>
1	32	32	32	32
2	40	20	72	52
3	66	22	138	74
4	116	29	254	103
5	140	28	394	131
6	114	19	508	150
7	112	16	620	166
8	128	16	748	182
9	63	7	811	189
10	40	4	851	193

Galton_counts %>%
  gf_col(No_of_families ~ nkids) %>%
  gf_theme(theme_classic())

Galton_counts %>%
  e_charts(nkids) %>%
  e_bar(No_of_families,
    colorBy = "data",
    legend = FALSE
  ) %>% # Or "series"

  # https://echarts4r.john-coene.com/articles/grid.html
  # echarts4r does not "automatically" name the axes!
  # And look at the "categorical" x-axis below!

  e_x_axis(
    name = "Family Size", nameLocation = "center",
    nameGap = 25, type = "category"
  ) %>%
  e_y_axis(name = "Count", nameLocation = "center", nameGap = 25, ) %>%
  e_tooltip(trigger = "item") %>%
  e_title("No of Families of each size")

Galton_counts %>%
  plot_ly(x = ~nkids, y = ~No_of_families) %>%
  add_bars()

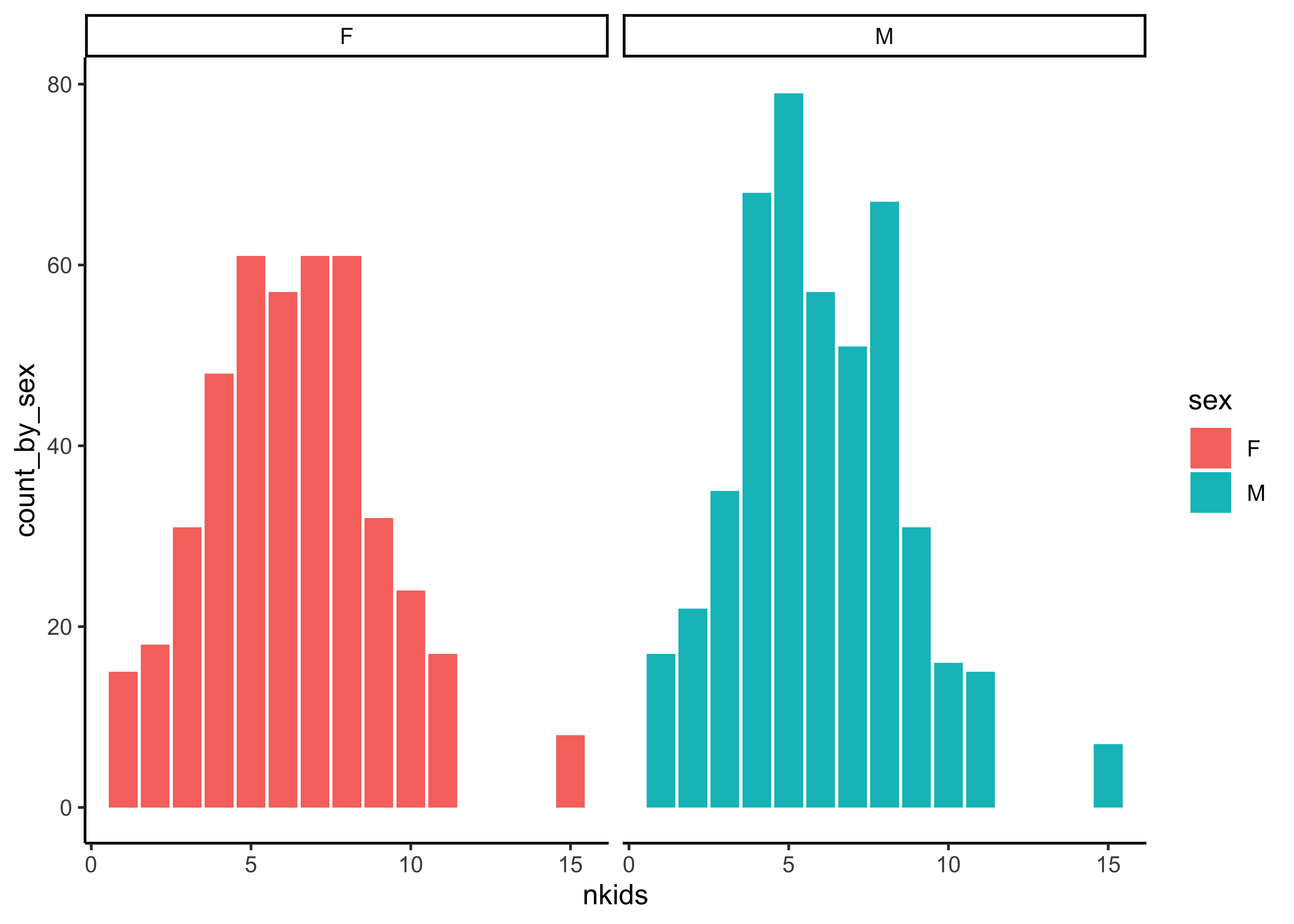
Insight: There are 32 1-kid families; and $128 / 8 = 16$ 8-kid families! There is one great great 15-kid family. (Did you get the idea behind why we divide here?)

Question

Q.2. What is the count of Children by sex of the child and by family size nkids?

Using ggformula
Using echarts4r

Galton_counts_by_sex <- Galton %>%
  mutate(family = as.integer(family)) %>%
  group_by(nkids, sex) %>%
  summarise(count_by_sex = n()) %>%
  ungroup() %>%
  group_by(sex)
Galton_counts_by_sex %>%
  gf_col(count_by_sex ~ nkids | sex, fill = ~sex, data = .)

Galton_counts_by_sex <- Galton %>%
  mutate(family = as.integer(family)) %>%
  group_by(nkids, sex) %>%
  summarise(count_by_sex = n()) %>%
  ungroup() %>%
  group_by(sex)
Galton_counts_by_sex

ABCDEFGHIJ0123456789

nkids <int>	sex <fct>	count_by_sex <int>
1	F	15
1	M	17
2	F	18
2	M	22
3	F	31
3	M	35
4	F	48
4	M	68
5	F	61
5	M	79

Galton_counts_by_sex %>%
  e_charts(nkids) %>%
  e_bar(count_by_sex) %>%
  e_x_axis(
    name = "Family Size (nkids)", nameLocation = "center",
    nameGap = 20, type = "category"
  ) %>%
  e_y_axis(
    name = "How Many Children?",
    nameGap = 20,
    nameTextStyle = list(align = "center"),
    nameLocation = "center"
  ) %>%
  e_legend(right = 25, orient = "vertical") %>%
  e_facet(cols = 2, rows = 1) %>%
  e_tooltip(trigger = "item") %>%
  e_title("Child Counts by Sex over Family Size")

Insight: Hmm…decent gender balance overall, across family sizes nkids.

Follow-up Question

Follow up Question: How would we look for “gender balance” in individual families? Should we look at the family column ?

Galton %>%
  mutate(family = as.integer(family)) %>%
  group_by(family, sex) %>%
  summarise(count_by_sex = n()) %>%
  ungroup() %>%
  group_by(sex) %>%
  e_charts(family) %>%
  e_bar(count_by_sex) %>%
  e_x_axis(
    name = "nkids", nameLocation = "center",
    nameGap = 25, type = "category"
  ) %>%
  e_y_axis(
    name = "How Many Children?",
    nameGap = 25, nameLocation = "center"
  ) %>%
  e_legend(right = 5) %>%
  e_facet(cols = 2, rows = 1) %>%
  e_tooltip(trigger = "item") %>%
  e_title("Child Counts by Sex over Family ID")

Insight: The No of Children were distributed similarly across family sizenkids… However, this plot is too crowded and does not lead to any great insight. Using family ID was silly to plot against, wasn’t it? Not all exploratory plots will be “necessary” in the end. But they are part of the journey of getting better acquainted with the data!

{{}} Stat Summaries and Distributions

OK, on to the Quantitative variables now! What Questions might we have, that could relate not to counts by Qual variables, but to the numbers in Quant variables. Stat measures, like their ranges, max and min? Means, medians, distributions? And how these vary on the basis of Qual variables? All this using histograms and densities.

Summary Stats

As Stigler(Stigler 2016) said, summaries are the first thing to look at in data. skimr::skim has already given us a lot summary data for Quant variables. We can now use mosaic::favstats to develop these further, by slicing / facetting these wrt other Qual variables. Let us tabulate some quick stat summaries of the important variables in Galton.

# summaries facetted by sex of child
measures <- favstats(~ height | sex, data = Galton)
measures

ABCDEFGHIJ0123456789

sex <chr>	min <dbl>	Q1 <dbl>	median <dbl>	Q3 <dbl>	max <dbl>	mean <dbl>	sd <dbl>	n <int>	missing <int>
F	56	62.5	64.0	65.5	70.5	64.11016	2.370320	433	0
M	60	67.5	69.2	71.0	79.0	69.22882	2.631594	465	0

Insight: We saw earlier that the mean height of the Children was 66 inches. However, are Sons taller than Daughters? Difference in mean height is 5 inches! AND…that was the same difference between fathers and mothers mean heights! Is it so simple then?

Question

Q.4 How are the heights of the children distributed? Here is where we need a e_histogram…

Galton %>%
  e_charts() %>%
  e_histogram(serie = height) %>%
  e_tooltip(trigger = "item") %>%
  e_mark_line(
    data = list(xAxis = mean(Galton$height)),
    label = list(
      label = "Mean Height",
      label.position = "end"
    ),
    lineStyle = list(
      color = "red", width = 1.5,
      type = "solid"
    )
  ) %>%
  # See https://echarts.apache.org/en/option.html#series-line.markLine

  e_x_axis(name = "Height", nameLocation = "center") %>%
  e_y_axis(name = "Counts", nameLocation = "center", nameGap = 30) %>%
  e_title("Distribution of Heights in Galton")

Insight: Fairly symmetric distribution…but there are a few very short and some very tall children! Try to change the no. of bins to check of we are missing some pattern. This is not completely easy with echarts4r which uses the “Sturges” algorithm to set the number of bins. Need to figure this out from the echarts Apache API docs.

Question

Q.5 Is there a difference in height distributions between Male and Female children?(Quant variable sliced by Qual variable)

We will use the raw Galton data and previously-computed measures:

Galton %>%
  group_by(sex) %>%
  e_charts(height = 300) %>%
  e_density(height) %>%
  e_mark_line(
    data = list(xAxis = measures %>% filter(sex == "M") %>%
      select(mean) %>% as.numeric()),
    # This code colours both v-lines red...how?
    lineStyle = list(
      color = "red", width = 1.5,
      type = "solid"
    )
  ) %>%
  # Upto here gives one line in red colour, correctly

  e_mark_line(
    data = list(xAxis = measures %>%
      filter(sex == "F") %>%
      select(mean) %>% as.numeric()),

    # This piece of code has no effect...wonder why not?
    # BOTH lines are in red ...why??
    lineStyle = list(
      color = "black", width = 1.5,
      type = "solid"
    )
  ) %>%
  e_title("Distributions of Height by Sex in Galton") %>%
  e_x_axis(name = "Height", nameLocation = "center") %>%
  e_legend(right = 5)

Insight: There is a visible difference in average heights between girls and boys. Is that significant, however? We will need a statistical inference test to figure that out!! Claus Wilke¹ says comparisons of Quant variables across groups are best made between densities and not histograms…

Question

Q.6 Are Mothers generally shorter than fathers?

Galton %>%
  e_charts(height = 300) %>%
  e_density(father) %>%
  e_density(mother) %>%
  e_mark_line(
    data = list(xAxis = mean(Galton$mother)),
    lineStyle = list(
      color = "red", width = 1.5,
      type = "solid"
    )
  ) %>%
  e_mark_line(data = list(
    xAxis = mean(Galton$father),
    lineStyle = list(
      color = "black", width = 1.5,
      type = "solid"
    )
  )) %>%
  e_legend(right = 10)

Insight: Yes, moms are on average shorter than dads in this dataset. Again, is this difference statistically significant? We will find out in when we do Inference.

Question

Q.7a. Are heights of children different based on the number of kids in the family? And For Male and Female children?

Galton %>%
  group_by(nkids) %>%
  e_charts(height = 400) %>%
  e_boxplot(height,
    colorBy = "data",
    itemStyle = list(borderWidth = 3)
  ) %>%
  e_y_axis(
    max = 80, min = 50, name = "height", nameLocation = "center",
    nameGap = 25, margin = 5
  ) %>% # adds +/- 5 to y-axis limits

  e_x_axis(
    name = "Family Size",
    nameLocation = "center",
    nameGap = 25, type = "category"
  ) %>% # makes a category axis showing factors

  e_tooltip() %>%
  e_title("Heights over Family Size")

Question

Q.7b. Are heights of children different for Male and Female children?

# Can do better at colouring/filling and facetting...
Galton %>%
  group_by(nkids, sex) %>%
  e_charts(height = 400) %>% # no x-variable needed for boxplots
  e_boxplot(height,
    colorBy = "data",
    itemStyle = list(borderWidth = 3)
  ) %>%
  e_y_axis(
    max = 80, min = 50, name = "height", nameLocation = "center",
    nameGap = 25, margin = 5
  ) %>% # adds +/- 5 to y-axis limits

  e_x_axis(
    name = "Family Size",
    nameLocation = "center",
    nameGap = 25, type = "category"
  ) %>% # makes a category axis showing factors

  e_tooltip() %>%
  e_title("Heights by Sex over Family Size")

Insight: So, at all family “strengths”, the male children are taller than the female children. Box plots are used to show distributions of numeric data values and compare them between multiple groups (i.e Categorical Data, here sex and nkids).

Question

Q.8 Does the mean height of children in a family vary with the number of children in the family? (family size)?

Galton %>%
  group_by(nkids) %>%
  summarise(mean_height = mean(height)) %>%
  e_charts(nkids, height = 300) %>%
  e_bar(mean_height, colorBy = "data", legend = FALSE) %>%
  e_x_axis(
    name = "nkids", nameLocation = "center", nameGap = 25,
    type = "category"
  ) %>%
  e_y_axis(name = "mean height", nameLocation = "center", nameGap = 25) %>%
  e_tooltip(trigger = "item")

Insight: Hmm…The graph shows that mean heights do not vary much with family size nkids. We saw this with the box plots earlier. This would be useful information in a Modelling and Prediction exercise.

Follow-up Question

Q. 8a. Is height difference between sons and daughters related to height difference between father and mother?

Differences between father and mother heights influencing height…this would be like height ~ (father-mother). This would be a relationship between two Quant variables. A histogram would not serve here and we plot this as a Scatter Plot:

Galton %>%
  group_by(family, sex) %>%
  # Parental Height Difference
  mutate(diff_height = father - mother) %>%
  select(family, sex, height, diff_height) %>%
  ungroup() %>%
  group_by(sex) %>%
  e_charts(diff_height, height = 300) %>%
  e_scatter(height, symbol_size = 8) %>%
  # Fit a trend line
  e_lm(height ~ diff_height,
    name = c("Female", "Male")
  ) %>%
  e_x_axis(
    max = 18, min = -5,
    name = "Father - Mother Height",
    nameLocation = "center", nameGap = 25
  ) %>%
  e_y_axis(
    max = 80, min = 50,
    name = "Children's Heights",
    nameLocation = "center", nameGap = 25
  ) %>%
  e_tooltip(axisPointer = list(type = "cross"))

Insight: There seems no relationship, or a very small one, between children’s heights on the y-axis and the difference in parental height differences on the x-axis…

And so on…..we can proceed from simple visualizations based on Questions to larger questions that demand inference and modelling. We hinted briefly on these in the above Case Study.

Case Study-2: Dataset from `NHANES`

Let us try the NHANES dataset.

Try help(NHANES) in your Console.

data("NHANES")

Look at the Data

skim(NHANES)

Data summary
Name	NHANES
Number of rows	10000
Number of columns	76
_______________________
Column type frequency:
factor	31
numeric	45
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
SurveyYr	0	1.00	FALSE	2	200: 5000, 201: 5000
Gender	0	1.00	FALSE	2	fem: 5020, mal: 4980
AgeDecade	333	0.97	FALSE	8	40: 1398, 0-: 1391, 10: 1374, 20: 1356
Race1	0	1.00	FALSE	5	Whi: 6372, Bla: 1197, Mex: 1015, Oth: 806
Race3	5000	0.50	FALSE	6	Whi: 3135, Bla: 589, Mex: 480, His: 350
Education	2779	0.72	FALSE	5	Som: 2267, Col: 2098, Hig: 1517, 9 -: 888
MaritalStatus	2769	0.72	FALSE	6	Mar: 3945, Nev: 1380, Div: 707, Liv: 560
HHIncome	811	0.92	FALSE	12	mor: 2220, 750: 1084, 250: 958, 350: 863
HomeOwn	63	0.99	FALSE	3	Own: 6425, Ren: 3287, Oth: 225
Work	2229	0.78	FALSE	3	Wor: 4613, Not: 2847, Loo: 311
BMICatUnder20yrs	8726	0.13	FALSE	4	Nor: 805, Obe: 221, Ove: 193, Und: 55
BMI_WHO	397	0.96	FALSE	4	18.: 2911, 30.: 2751, 25.: 2664, 12.: 1277
Diabetes	142	0.99	FALSE	2	No: 9098, Yes: 760
HealthGen	2461	0.75	FALSE	5	Goo: 2956, Vgo: 2508, Fai: 1010, Exc: 878
LittleInterest	3333	0.67	FALSE	3	Non: 5103, Sev: 1130, Mos: 434
Depressed	3327	0.67	FALSE	3	Non: 5246, Sev: 1009, Mos: 418
SleepTrouble	2228	0.78	FALSE	2	No: 5799, Yes: 1973
PhysActive	1674	0.83	FALSE	2	Yes: 4649, No: 3677
TVHrsDay	5141	0.49	FALSE	7	2_h: 1275, 1_h: 884, 3_h: 836, 0_t: 638
CompHrsDay	5137	0.49	FALSE	7	0_t: 1409, 0_h: 1073, 1_h: 1030, 2_h: 589
Alcohol12PlusYr	3420	0.66	FALSE	2	Yes: 5212, No: 1368
SmokeNow	6789	0.32	FALSE	2	No: 1745, Yes: 1466
Smoke100	2765	0.72	FALSE	2	No: 4024, Yes: 3211
Smoke100n	2765	0.72	FALSE	2	Non: 4024, Smo: 3211
Marijuana	5059	0.49	FALSE	2	Yes: 2892, No: 2049
RegularMarij	5059	0.49	FALSE	2	No: 3575, Yes: 1366
HardDrugs	4235	0.58	FALSE	2	No: 4700, Yes: 1065
SexEver	4233	0.58	FALSE	2	Yes: 5544, No: 223
SameSex	4232	0.58	FALSE	2	No: 5353, Yes: 415
SexOrientation	5158	0.48	FALSE	3	Het: 4638, Bis: 119, Hom: 85
PregnantNow	8304	0.17	FALSE	3	No: 1573, Yes: 72, Unk: 51

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
ID	0	1.00	61944.64	5871.17	51624.00	56904.50	62159.50	67039.00	71915.00	▇▇▇▇▇
Age	0	1.00	36.74	22.40	0.00	17.00	36.00	54.00	80.00	▇▇▇▆▅
AgeMonths	5038	0.50	420.12	259.04	0.00	199.00	418.00	624.00	959.00	▇▇▇▆▃
HHIncomeMid	811	0.92	57206.17	33020.28	2500.00	30000.00	50000.00	87500.00	100000.00	▃▆▃▁▇
Poverty	726	0.93	2.80	1.68	0.00	1.24	2.70	4.71	5.00	▅▅▃▃▇
HomeRooms	69	0.99	6.25	2.28	1.00	5.00	6.00	8.00	13.00	▂▆▇▂▁
Weight	78	0.99	70.98	29.13	2.80	56.10	72.70	88.90	230.70	▂▇▂▁▁
Length	9457	0.05	85.02	13.71	47.10	75.70	87.00	96.10	112.20	▁▃▆▇▃
HeadCirc	9912	0.01	41.18	2.31	34.20	39.58	41.45	42.92	45.40	▁▂▇▇▅
Height	353	0.96	161.88	20.19	83.60	156.80	166.00	174.50	200.40	▁▁▁▇▂
BMI	366	0.96	26.66	7.38	12.88	21.58	25.98	30.89	81.25	▇▆▁▁▁
Pulse	1437	0.86	73.56	12.16	40.00	64.00	72.00	82.00	136.00	▂▇▃▁▁
BPSysAve	1449	0.86	118.15	17.25	76.00	106.00	116.00	127.00	226.00	▃▇▂▁▁
BPDiaAve	1449	0.86	67.48	14.35	0.00	61.00	69.00	76.00	116.00	▁▁▇▇▁
BPSys1	1763	0.82	119.09	17.50	72.00	106.00	116.00	128.00	232.00	▂▇▂▁▁
BPDia1	1763	0.82	68.28	13.78	0.00	62.00	70.00	76.00	118.00	▁▁▇▆▁
BPSys2	1647	0.84	118.48	17.49	76.00	106.00	116.00	128.00	226.00	▃▇▂▁▁
BPDia2	1647	0.84	67.66	14.42	0.00	60.00	68.00	76.00	118.00	▁▁▇▆▁
BPSys3	1635	0.84	117.93	17.18	76.00	106.00	116.00	126.00	226.00	▃▇▂▁▁
BPDia3	1635	0.84	67.30	14.96	0.00	60.00	68.00	76.00	116.00	▁▁▇▇▁
Testosterone	5874	0.41	197.90	226.50	0.25	17.70	43.82	362.41	1795.60	▇▂▁▁▁
DirectChol	1526	0.85	1.36	0.40	0.39	1.09	1.29	1.58	4.03	▅▇▂▁▁
TotChol	1526	0.85	4.88	1.08	1.53	4.11	4.78	5.53	13.65	▂▇▁▁▁
UrineVol1	987	0.90	118.52	90.34	0.00	50.00	94.00	164.00	510.00	▇▅▂▁▁
UrineFlow1	1603	0.84	0.98	0.95	0.00	0.40	0.70	1.22	17.17	▇▁▁▁▁
UrineVol2	8522	0.15	119.68	90.16	0.00	52.00	95.00	171.75	409.00	▇▆▃▂▁
UrineFlow2	8524	0.15	1.15	1.07	0.00	0.48	0.76	1.51	13.69	▇▁▁▁▁
DiabetesAge	9371	0.06	48.42	15.68	1.00	40.00	50.00	58.00	80.00	▁▂▆▇▂
DaysPhysHlthBad	2468	0.75	3.33	7.40	0.00	0.00	0.00	3.00	30.00	▇▁▁▁▁
DaysMentHlthBad	2466	0.75	4.13	7.83	0.00	0.00	0.00	4.00	30.00	▇▁▁▁▁
nPregnancies	7396	0.26	3.03	1.80	1.00	2.00	3.00	4.00	32.00	▇▁▁▁▁
nBabies	7584	0.24	2.46	1.32	0.00	2.00	2.00	3.00	12.00	▇▅▁▁▁
Age1stBaby	8116	0.19	22.65	4.77	14.00	19.00	22.00	26.00	39.00	▆▇▅▂▁
SleepHrsNight	2245	0.78	6.93	1.35	2.00	6.00	7.00	8.00	12.00	▁▅▇▁▁
PhysActiveDays	5337	0.47	3.74	1.84	1.00	2.00	3.00	5.00	7.00	▇▇▃▅▅
TVHrsDayChild	9347	0.07	1.94	1.43	0.00	1.00	2.00	3.00	6.00	▇▆▂▂▂
CompHrsDayChild	9347	0.07	2.20	2.52	0.00	0.00	1.00	6.00	6.00	▇▁▁▁▃
AlcoholDay	5086	0.49	2.91	3.18	1.00	1.00	2.00	3.00	82.00	▇▁▁▁▁
AlcoholYear	4078	0.59	75.10	103.03	0.00	3.00	24.00	104.00	364.00	▇▁▁▁▁
SmokeAge	6920	0.31	17.83	5.33	6.00	15.00	17.00	19.00	72.00	▇▂▁▁▁
AgeFirstMarij	7109	0.29	17.02	3.90	1.00	15.00	16.00	19.00	48.00	▁▇▂▁▁
AgeRegMarij	8634	0.14	17.69	4.81	5.00	15.00	17.00	19.00	52.00	▂▇▁▁▁
SexAge	4460	0.55	17.43	3.72	9.00	15.00	17.00	19.00	50.00	▇▅▁▁▁
SexNumPartnLife	4275	0.57	15.09	57.85	0.00	2.00	5.00	12.00	2000.00	▇▁▁▁▁
SexNumPartYear	5072	0.49	1.34	2.78	0.00	1.00	1.00	1.00	69.00	▇▁▁▁▁

Again, lots of data from skim, about the Quant and Qual variables. Spend a little time looking through this output.

Which variables could have been data that was given/stated by each respondent?
And which ones could have been measured dependent data variables? Why do you think so?
Why is there so much missing data? Which variable are the most affected by this?

Counts, and Charts with Counts

Question

Q.1 What are the Education levels and the counts of people with those levels?

NHANES %>%
  group_by(Education) %>%
  summarise(total = n())

ABCDEFGHIJ0123456789

Education <fct>	total <int>
8th Grade	451
9 - 11th Grade	888
High School	1517
Some College	2267
College Grad	2098
NA	2779

# This also works
# tally(~Education, data = NHANES) %>% as_tibble()

Insight: The count goes up as we go from lower Education levels to higher. Need to keep that in mind. How do we understand the large number of NA entries?

Question

Q.2 How do counts of Education vs Work-status look like?

NHANES %>%
  mutate(Education = as.factor(Education)) %>%
  group_by(Work, Education) %>%
  summarise(count = n())
NHANES %>%
  group_by(Work, Education) %>%
  summarise(count = n()) %>%
  e_charts(Education, height = 300) %>%
  e_bar(count) %>%
  e_y_axis(max = 1750) %>%
  e_x_axis(type = "category") %>%
  e_tooltip()

ABCDEFGHIJ0123456789

Work <fct>	Education <fct>
Looking	8th Grade
Looking	9 - 11th Grade
Looking	High School
Looking	Some College
Looking	College Grad
Looking	NA
NotWorking	8th Grade
NotWorking	9 - 11th Grade
NotWorking	High School
NotWorking	Some College

Insight: Clear increase in the number of Working people as Education goes from 8th Grade to College. No surprise. Are the NotWorking counts a surprise?

{{}} Stat Summaries, Histograms, and Densities

Question

Q.3. What is the distribution of Physical Activity Days, across Gender? Across Education?

# NHANES %>% gf_histogram( ~ PhysActiveDays | Education, fill = ~ Education)
NHANES %>%
  group_by(Gender) %>%
  e_charts(PhysActiveDays, height = 350) %>%
  e_histogram(PhysActiveDays) %>%
  e_x_axis(max = 8) %>%
  e_facet(cols = 2, rows = 1) %>%
  e_tooltip()
NHANES %>%
  group_by(Education) %>%
  e_charts(PhysActiveDays, height = 350) %>%
  e_histogram(PhysActiveDays) %>%
  e_x_axis(max = 8) %>%
  e_facet(rows = 1, cols = 3) %>%
  e_tooltip()

Insight: Can we conclude anything here? The populations in each category are different, as indicated by the different y-axis scales, so what do we need to do? Take percentages or ratios of course, per-capita! How would one do that?

Question

Q.3a. What is the distribution of Physical Activity Days, across Education and Sex, per capita?

NHANES %>%
  group_by(Gender) %>%
  summarize(mean_active = mean(PhysActiveDays, na.rm = TRUE))
NHANES %>%
  group_by(Education) %>%
  summarize(mean_active = mean(PhysActiveDays, na.rm = TRUE))

ABCDEFGHIJ0123456789

Gender <fct>	mean_active <dbl>
female	3.813687
male	3.677231

ABCDEFGHIJ0123456789

Education <fct>	mean_active <dbl>
8th Grade	3.844311
9 - 11th Grade	3.581197
High School	3.676800
Some College	3.514706
College Grad	3.856916
NA	3.927667

Insight: Hmm..no great differences in per-capita physical activity. Females are marginally more active than males. No need to even plot this.

Question

Q.4. How are people Ages distributed across levels of Education?

# Recall there are missing data
# gf_boxplot(Age ~ Education,
#            fill = ~ Education, # Always a good idea to fill boxes
#            data = NHANES) %>%
#   gf_theme(theme_classic()) %>% plotly::ggplotly()

NHANES %>%
  mutate(Education = as.factor(Education)) %>%
  group_by(Education) %>%
  e_charts(height = 300) %>% # Should not mention x-variable!!!
  e_boxplot(Age,
    colorBy = "data",
    itemStyle = list(borderWidth = 3)
  ) %>%
  e_y_axis(name = "Age", nameLocation = "middle", max = 100, min = 0, nameGap = 25) %>%
  e_x_axis(
    type = "category", axisTick = list(alignWithLabel = TRUE),
    axisLabel = list(interval = 0)
  ) %>% # ensures all tick labels on x-axis
  e_tooltip()

Insight: Older age groups are somewhat more heavily represented in groups with lower educational status. But College Graduates also have slightly older age distributions…So do College Educated people live longer? That is a nice Question for some Inferential Modelling. And how to interpret the NA group?

Question

Q.5. How is Education distributed over Race?

NHANES_by_Race1 <- NHANES %>%
  group_by(Race1) %>%
  summarize(population = n())
NHANES_by_Race1
NHANES %>%
  group_by(Education, Race1) %>%
  summarize(n = n()) %>%
  left_join(NHANES_by_Race1, by = c("Race1" = "Race1")) %>%
  mutate(percapita_educated = (n / population) * 100) %>%
  ungroup() %>%
  group_by(Race1) %>% # Aesthetic 1
  e_charts(Education, height = 350) %>% # Aesthetic #2
  e_bar(percapita_educated) %>% # Aesthetic #3

  e_x_axis(
    type = "category", axisTick = list(alignWithLabel = TRUE),
    axisLabel = list(interval = 0)
  ) %>%
  e_y_axis(max = 35) %>%
  e_facet(rows = 2, cols = 3) %>%
  e_flip_coords()

ABCDEFGHIJ0123456789

Race1 <fct>	population <int>
Black	1197
Hispanic	610
Mexican	1015
White	6372
Other	806

Insight: Blacks, Hispanics, and Mexicans tend to have fewer people with college degrees, as a percentage of their population. Asians and other immigrants have a significant tendency towards higher education!

Question

Q.6. What is the distribution of people’s BMI, split by Gender? By Race1?

# One can also plot both histograms and densities in an overlay fashion,

NHANES %>%
  group_by(Gender) %>%
  e_charts(height = 300) %>%
  e_density(BMI)
NHANES %>%
  group_by(Race1) %>%
  e_charts(height = 350) %>%
  e_density(BMI) %>%
  e_facet(rows = 2, cols = 3)

Insight: Non-white races tend to have larger portions of their populations with larger BMI. So these races perhaps tend to obesity. By and large BMI distributions are normal.

Question

Q.7. What is the distribution of people’s Testosterone level vs BMI? Split By Race1?

NHANES %>%
  gf_density2d(Testosterone ~ BMI | Race1) %>%
  gf_theme(theme_classic()) %>%
  plotly::ggplotly()

Insight: Low testosterone levels exist across all BMI values, but healthy levels of T exists only over a smaller range of BMI.

Note: echarts4r does not seem to provide a 2D-density plot…yet!!

Case Study #3: A complete example with Banned Books

Here is a dataset from Jeremy Singer-Vine’s blog, Data Is Plural. This is a list of all books banned in schools across the US.

Look at the Data

banned <- readxl::read_xlsx(
  path = "../data/banned.xlsx",
  sheet = "Sorted by Author & Title"
)
skim(banned)

Data summary
Name	banned
Number of rows	1586
Number of columns	10
_______________________
Column type frequency:
character	10
________________________
Group variables	None

Variable type: character

skim_variable	n_missing	complete_rate	min	max	n_unique
Author	0	1.00	7	29	797
Title	0	1.00	2	155	1145
Type of Ban	0	1.00	21	36	4
Secondary Author(s)	1488	0.06	9	187	61
Illustrator(s)	1222	0.23	8	35	192
Translator(s)	1576	0.01	14	25	9
State	0	1.00	4	14	26
District	0	1.00	4	40	86
Date of Challenge/Removal	0	1.00	5	15	15
Origin of Challenge	0	1.00	13	16	2

Insight: Clearly the variables are all Qualitative, except perhaps for Date of Challenge/Removal, (which in this case has been badly mangled by Excel) So we need to make counts based on the* levels* of the Qual variables and plot Bar/Column charts. We will not find a use for histograms or densities.

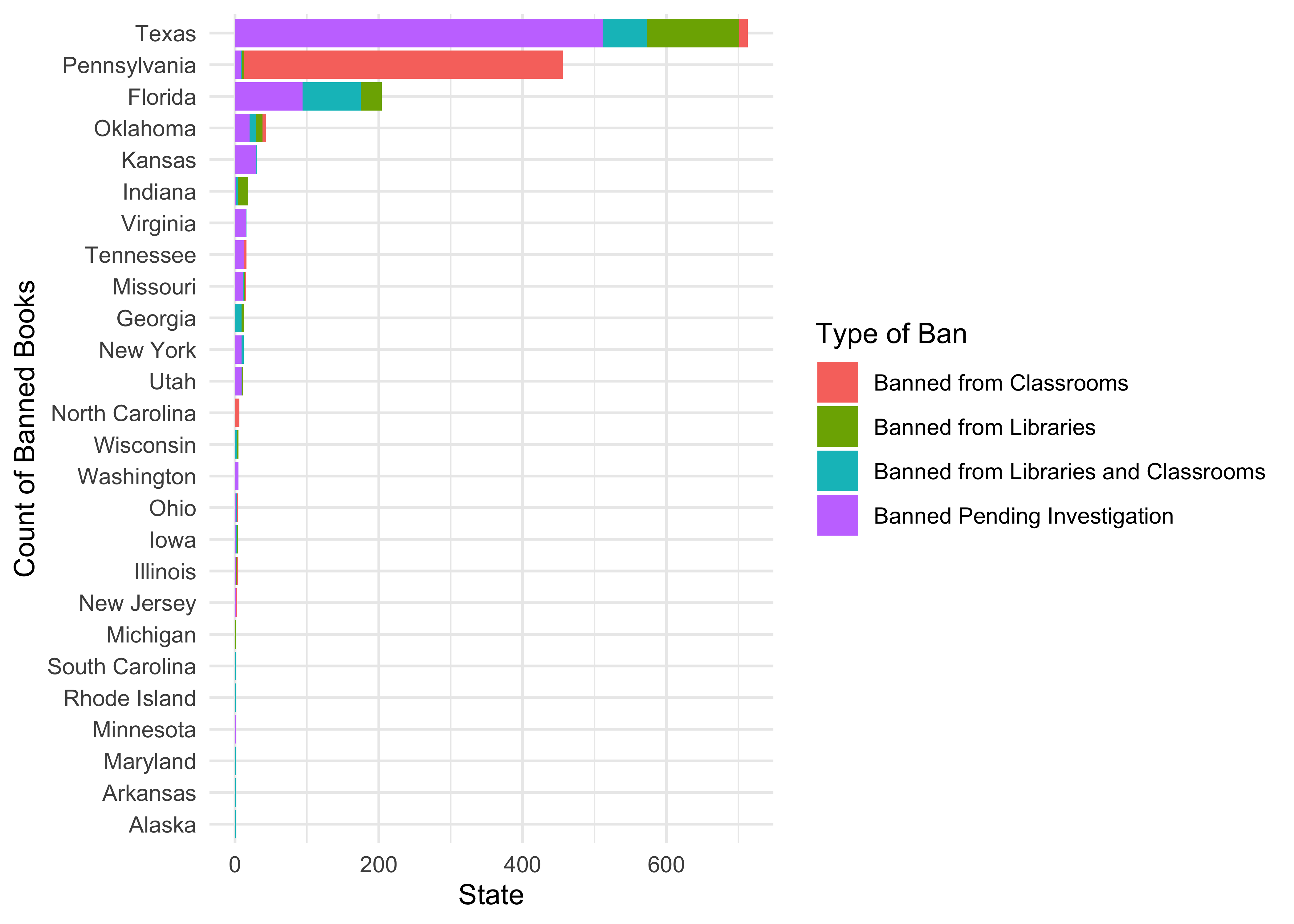
Let us try to answer this question, about counts:

Question

What is the count of banned books by type and by US state?

banned_by_state <-
  banned %>%
  group_by(State) %>%
  summarise(total = n()) %>%
  ungroup()
banned_by_state

ABCDEFGHIJ0123456789

State <chr>	total <int>
Alaska	1
Arkansas	1
Florida	204
Georgia	13
Illinois	4
Indiana	18
Iowa	4
Kansas	30
Maryland	1
Michigan	2

banned %>%
  group_by(State, `Type of Ban`) %>%
  summarise(count = n()) %>%
  ungroup() %>%
  left_join(., banned_by_state, by = c("State" = "State")) %>%
  #  pivot_wider(.,id_cols = State,
  #              names_from = `Type of Ban`,
  #              values_from = count) %>% janitor::clean_names() %>%
  #  replace_na(list(banned_from_libraries_and_classrooms = 0,
  #                  banned_from_libraries = 0,
  #                  banned_pending_investigation = 0,
  #                  banned_from_classrooms = 0)) %>%
  # mutate(total = sum(across(where(is.integer)))) %>%
  gf_col(count ~ reorder(State, total),
    fill = ~`Type of Ban`
  ) %>%
  gf_labs(
    x = "Count of Banned Books",
    y = "State"
  ) %>%
  gf_refine(coord_flip()) %>%
  gf_theme(theme = theme_minimal())

Insight: Do you want to live in Texas? If you are both illiterate and interested in horses, perhaps.

Conclusion

And that is a wrap!! Try to work with this procedure:

Inspect the data using skim or inspect
Identify Qualitative and Quantitative variables
Notice variables that have missing data
Develop Counts of Observations for combinations of Qualitative variables (factors)
Develop Histograms and Densities, and slice them by Qualitative variables to develop facetted plots as needed
At each step record the insight and additional questions!!
Continue with other Descriptive Graphs as needed
And then on the inference and modelling!!

References

Sharon Machlis, Plot in R with echarts4r, InfoWorld https://www.infoworld.com/article/3607068/plot-in-r-with-echarts4r.html
A detailed analysis of the NHANES dataset, https://awagaman.people.amherst.edu/stat230/Stat230CodeCompilationExampleCodeUsingNHANES.pdf

References

Stigler, Stephen M. 2016. “The Seven Pillars of Statistical Wisdom,” March. https://doi.org/10.4159/9780674970199.

Footnotes

Fundamentals of Data Visualization (clauswilke.com)↩︎

Setup the Packages

Introduction

Case Study-1: Galton Dataset from mosaicData

Look at the Data:

Counts, and Charts with Counts

{{}} Stat Summaries and Distributions

Case Study-2: Dataset from NHANES

Look at the Data

Counts, and Charts with Counts

{{}} Stat Summaries, Histograms, and Densities

Case Study #3: A complete example with Banned Books

Look at the Data

Conclusion

References

References

Footnotes

Case Study-1: Galton Dataset from `mosaicData`

Case Study-2: Dataset from `NHANES`