Quantities

How many of this and that?

Quant Variables

Histograms

Mean

Author

Arvind V.

Published

November 15, 2022

Modified

October 20, 2024

Abstract

Quant and Qual Variable Graphs and their Siblings

Slides and Tutorials

R (Static Viz)

Radiant Tutorial

Datasets

“The fear of death follows from the fear of life. A man who lives fully is prepared to die at any time.”

— Mark Twain

Setting up R Packages

library(tidyverse)
library(mosaic)
library(ggformula)
library(skimr)
##
library(crosstable) # Fast stats for multiple variables in table form

What graphs will we see today?

Variable #1	Variable #2	Chart Names	Chart Shape
Quant	None	Histogram

What kind of Data Variables will we choose?

No	Pronoun	Answer	Variable/Scale	Example	What Operations?
1	How Many / Much / Heavy? Few? Seldom? Often? When?	Quantities, with Scale and a Zero Value.Differences and Ratios /Products are meaningful.	Quantitative/Ratio	Length,Height,Temperature in Kelvin,Activity,Dose Amount,Reaction Rate,Flow Rate,Concentration,Pulse,Survival Rate	Correlation

Inspiration

Figure 1: Golf Drive Distance over the years

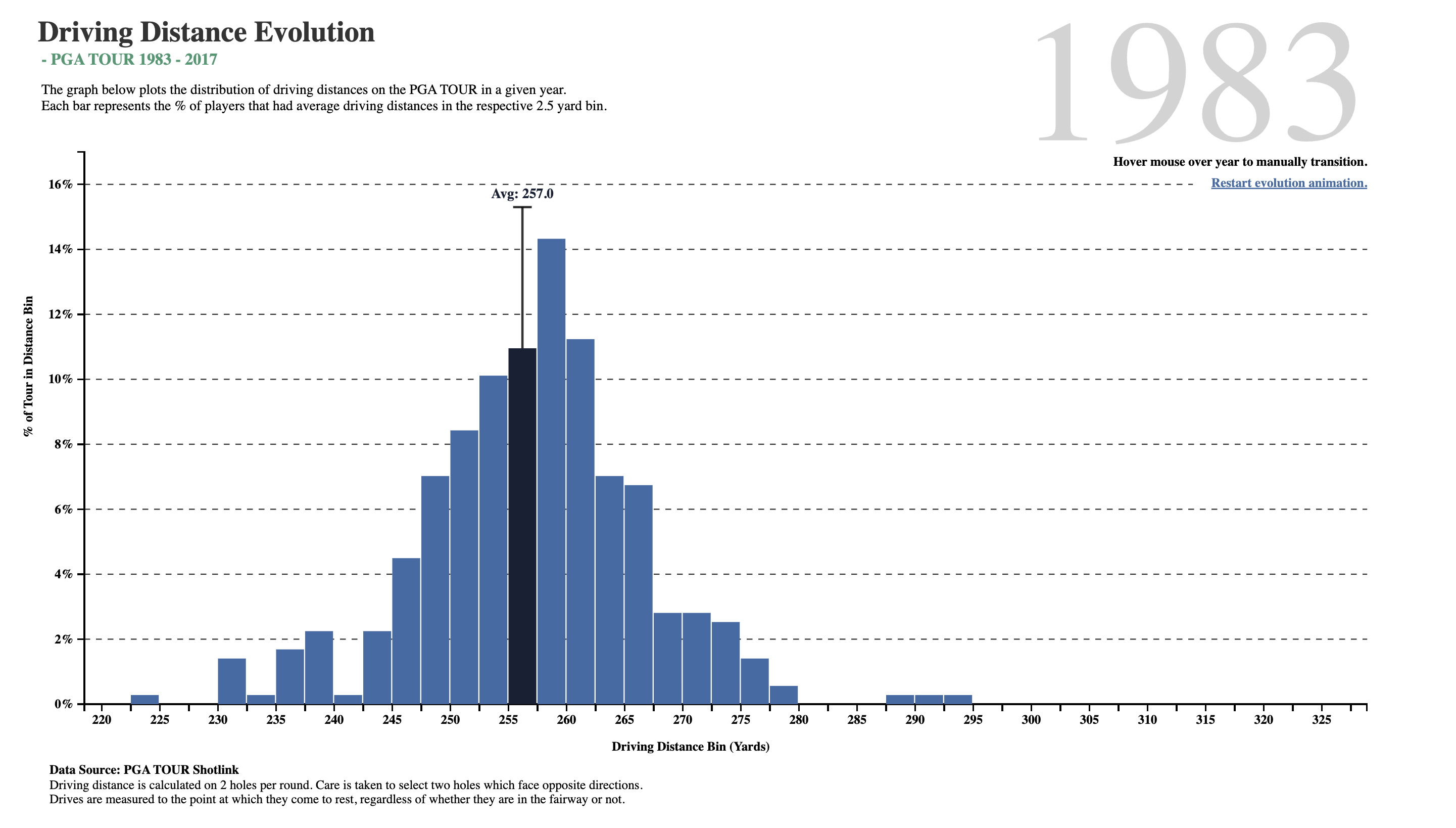
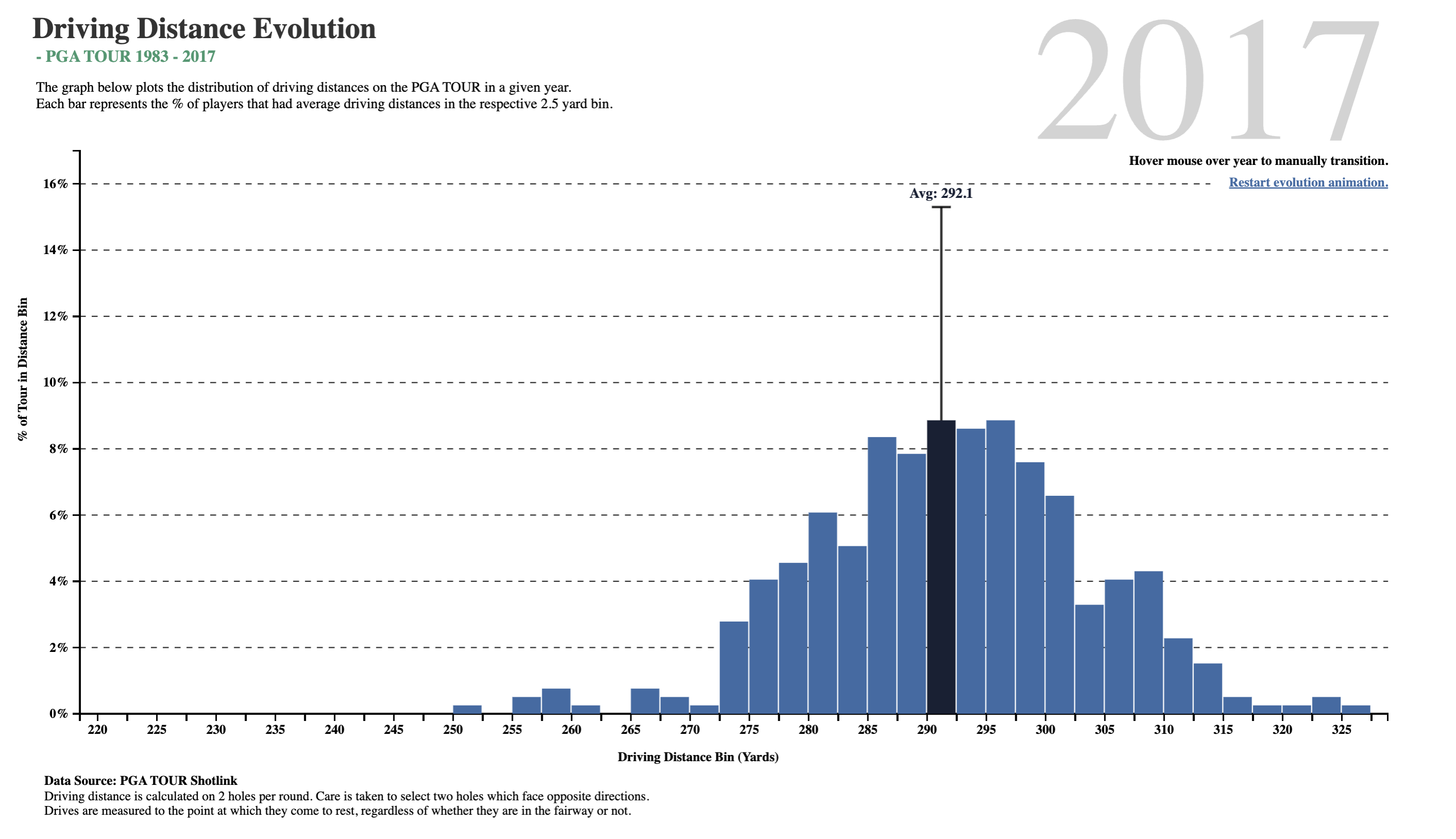
What do we see here? In about two-and-a-half decades, golf drive distances have increased, on the average, by 35 yards. The maximum distance has also gone up by 30 yards, and the minimum is now at 250 yards, which was close to average in 1983! What was a decent average in 1983 is just the bare minimum in 2017!!

Is it the dimples that the golf balls have? But these have been around a long time…or is it the clubs, and the swing technique invented by more recent players?

Now, let us listen to the late great Hans Rosling from the Gapminder Project, which aims at telling stories of the world with data, to remove systemic biases about poverty, income and gender related issues.

How do Histograms Work?

Histograms are best to show the distribution of raw Quantitative data, by displaying the number of values that fall within defined ranges, often called buckets or bins. We use a Quant variable on the x-axis and the histogram shows us how frequently different values occur for that variable by showing counts/frequencies on the y-axis. The x-axis is typically broken up into “buckets” or ranges for the x-variable. And usually you can adjust the bucket ranges to explore frequency patterns. For example, you can widen histogram buckets from 0-1, 1-2, 2-3, etc. to 0-2, 2-4, etc.

Although Bar Charts may look similar to Histograms, the two are different. Bar Charts show counts of observations with respect to a Qualitative variable. For instance, bar charts show categorical data with multiple levels, such as fruits, clothing, household products in an inventory. Each bar has a height proportional to the count per shirt-size, in this example.

Histograms do not usually show spaces between buckets because the buckets represent contiguous ranges, while bar charts show spaces to separate each (unconnected) category/level within a Qual variable.

Case Study-1: `diamonds` dataset

We will first look at at a dataset that is directly available in R, the diamonds dataset.

Examine the Data

As per our Workflow, we will look at the data using all the three methods we have seen.

R
web-r

glimpse(diamonds)

Rows: 53,940
Columns: 10
$ carat   <dbl> 0.23, 0.21, 0.23, 0.29, 0.31, 0.24, 0.24, 0.26, 0.22, 0.23, 0.…
$ cut     <ord> Ideal, Premium, Good, Premium, Good, Very Good, Very Good, Ver…
$ color   <ord> E, E, E, I, J, J, I, H, E, H, J, J, F, J, E, E, I, J, J, J, I,…
$ clarity <ord> SI2, SI1, VS1, VS2, SI2, VVS2, VVS1, SI1, VS2, VS1, SI1, VS1, …
$ depth   <dbl> 61.5, 59.8, 56.9, 62.4, 63.3, 62.8, 62.3, 61.9, 65.1, 59.4, 64…
$ table   <dbl> 55, 61, 65, 58, 58, 57, 57, 55, 61, 61, 55, 56, 61, 54, 62, 58…
$ price   <int> 326, 326, 327, 334, 335, 336, 336, 337, 337, 338, 339, 340, 34…
$ x       <dbl> 3.95, 3.89, 4.05, 4.20, 4.34, 3.94, 3.95, 4.07, 3.87, 4.00, 4.…
$ y       <dbl> 3.98, 3.84, 4.07, 4.23, 4.35, 3.96, 3.98, 4.11, 3.78, 4.05, 4.…
$ z       <dbl> 2.43, 2.31, 2.31, 2.63, 2.75, 2.48, 2.47, 2.53, 2.49, 2.39, 2.…

skim(diamonds)

Data summary
Name	diamonds
Number of rows	53940
Number of columns	10
_______________________
Column type frequency:
factor	3
numeric	7
________________________
Group variables	None

Variable type: factor

skim_variable	complete_rate	ordered	n_unique	top_counts
cut	1	TRUE	5	Ide: 21551, Pre: 13791, Ver: 12082, Goo: 4906
color	1	TRUE	7	G: 11292, E: 9797, F: 9542, H: 8304
clarity	1	TRUE	8	SI1: 13065, VS2: 12258, SI2: 9194, VS1: 8171

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
carat	1	0.80	0.47	0.2	0.40	0.70	1.04	5.01	▇▂▁▁▁
depth	1	61.75	1.43	43.0	61.00	61.80	62.50	79.00	▁▁▇▁▁
table	1	57.46	2.23	43.0	56.00	57.00	59.00	95.00	▁▇▁▁▁
price	1	3932.80	3989.44	326.0	950.00	2401.00	5324.25	18823.00	▇▂▁▁▁
x	1	5.73	1.12	0.0	4.71	5.70	6.54	10.74	▁▁▇▃▁
y	1	5.73	1.14	0.0	4.72	5.71	6.54	58.90	▇▁▁▁▁
z	1	3.54	0.71	0.0	2.91	3.53	4.04	31.80	▇▁▁▁▁

inspect(diamonds)


categorical variables:  
     name   class levels     n missing
1     cut ordered      5 53940       0
2   color ordered      7 53940       0
3 clarity ordered      8 53940       0
                                   distribution
1 Ideal (40%), Premium (25.6%) ...             
2 G (20.9%), E (18.2%), F (17.7%) ...          
3 SI1 (24.2%), VS2 (22.7%), SI2 (17%) ...      

quantitative variables:  
   name   class   min     Q1  median      Q3      max         mean           sd
1 carat numeric   0.2   0.40    0.70    1.04     5.01    0.7979397    0.4740112
2 depth numeric  43.0  61.00   61.80   62.50    79.00   61.7494049    1.4326213
3 table numeric  43.0  56.00   57.00   59.00    95.00   57.4571839    2.2344906
4 price integer 326.0 950.00 2401.00 5324.25 18823.00 3932.7997219 3989.4397381
5     x numeric   0.0   4.71    5.70    6.54    10.74    5.7311572    1.1217607
6     y numeric   0.0   4.72    5.71    6.54    58.90    5.7345260    1.1421347
7     z numeric   0.0   2.91    3.53    4.04    31.80    3.5387338    0.7056988
      n missing
1 53940       0
2 53940       0
3 53940       0
4 53940       0
5 53940       0
6 53940       0
7 53940       0

Data Dictionary

Quantitative Data

carat(dbl): weight of the diamond 0.2-5.01
depth(dbl): depth total depth percentage 43-79
table(dbl): width of top of diamond relative to widest point 43-95
price(dbl): price in US dollars $326-$18,823
x(dbl): length in mm 0-10.74
y(dbl): width in mm 0-58.9
z(dbl): depth in mm 0-31.8

Qualitative Data

cut: diamond cut Fair, Good, Very Good, Premium, Ideal
color: diamond color J (worst) to D (best). (7 levels)
clarity. measurement of how clear the diamond is I1 (worst), SI2, SI1, VS2, VS1, VVS2, VVS1, IF (best).

These have 5, 7, and 8 levels respectively. The fact that the class for these is ordered suggests that these are factors and that the levels have a sequence/order.

Business Insights on Examining the diamonds dataset

This is a large dataset (54K rows).
There are several Qualitative variables:
carat, price, x, y, z, depth and table are Quantitative variables.
There are no missing values for any variable, all are complete with 54K entries.

Hypothesis and Research Questions

Let us formulate a few Questions about this dataset. At some point, we might develop a hunch or two, and these would become our hypotheses to investigate. This is an iterative process!

Hypothesis and Research Questions

The target variable for an experiment that resulted in this data might be the price variable. Which is a numerical Quant variable.
There are also predictor variables such as carat (Quant), color(Qual), cut(Qual), and clarity(Qual).
Other predictor variables might be x, y, depth, table(all Quant)
Research Questions:
- What is the distribution of the target variable price?
- What is the distribution of the predictor variable carat?
- Does a price distribution vary based upon type of cut, clarity, and color?

These should do for now. Try and think of more Questions!

Plotting Histograms

Let’s plot some histograms to answer each of the Hypothesis questions above.

Question-1: What is the distribution of the target variable `price`?

Question-1: What is the distribution of the target variable price?

## Set graph theme
theme_set(new = theme_custom())
##
gf_histogram(~price, data = diamonds) %>%
  gf_labs(
    title = "Plot 1A: Diamond Prices",
    caption = "ggformula"
  )

## Set graph theme
theme_set(new = theme_custom())
## More bins
gf_histogram(~price,
  data = diamonds,
  bins = 100
) %>%
  gf_labs(
    title = "Plot 1B: Diamond Prices",
    caption = "ggformula"
  )

## Set graph theme
theme_set(new = theme_custom())
##

ggplot(data = diamonds) +
  geom_histogram(aes(x = price)) +
  labs(
    title = "Plot 1A: Diamond Prices",
    caption = "ggplot"
  )

## More bins
ggplot(data = diamonds) +
  geom_histogram(aes(x = price), bins = 100) +
  labs(
    title = "Plot 1B: Diamond Prices",
    caption = "ggplot"
  )

Business Insights-1

The price distribution is heavily skewed to the right.
There are a great many diamonds at relatively low prices, but there are a good few diamonds at very high prices too.
Using a high number of bins does not materially change the view of the histogram.

Question-2: What is the distribution of the predictor variable `carat`?

Question-1: Question-2: What is the distribution of the predictor variable carat?

## Set graph theme
theme_set(new = theme_custom())
##
diamonds %>%
  gf_histogram(~carat) %>%
  gf_labs(
    title = "Plot 2A: Carats of Diamonds",
    caption = "ggformula"
  )

## Set graph theme
theme_set(new = theme_custom())
## More bins
diamonds %>%
  gf_histogram(~carat,
    bins = 100
  ) %>%
  gf_labs(
    title = "Plot 2B: Carats of Diamonds",
    caption = "ggformula"
  )

theme_set(new = theme_custom())
#
diamonds %>%
  ggplot() +
  geom_histogram(aes(x = carat)) +
  labs(
    title = "Plot 2A: Carats of Diamonds",
    caption = "ggplot"
  )
## More bins
diamonds %>%
  ggplot() +
  geom_histogram(aes(x = carat), bins = 100) +
  labs(
    title = "Plot 2A: Carats of Diamonds",
    caption = "ggplot"
  )

Business Insights-2

carat also has a heavily right-skewed distribution.
However, there is a marked “discreteness” to the distribution. Some values of carat are far more common than others. For example, 1, 1.5, and 2 carat diamonds are large in number.
Why does the X-axis extend up to 5 carats? There must be some, very few, diamonds of very high carat value!

Question-3: Does a `price` distribution vary based upon type of `cut`, `clarity`, and `color`?

Does a price distribution vary based upon type of cut, clarity, and color?

## Set graph theme
theme_set(new = theme_custom())
##
gf_histogram(~price, fill = ~cut, data = diamonds) %>%
  gf_labs(title = "Plot 3A: Diamond Prices", caption = "ggformula")

diamonds %>%
  gf_histogram(~price, fill = ~cut, color = "black", alpha = 0.3) %>%
  gf_labs(
    title = "Plot 3B: Prices by Cut",
    caption = "ggformula"
  )

diamonds %>%
  gf_histogram(~price, fill = ~cut, color = "black", alpha = 0.3) %>%
  gf_facet_wrap(~cut) %>%
  gf_labs(
    title = "Plot 3C: Prices by Filled and Facetted by Cut",
    caption = "ggformula"
  ) %>%
  gf_theme(theme(
    axis.text.x = element_text(
      angle = 45,
      hjust = 1
    )
  ))

diamonds %>%
  gf_histogram(~price, fill = ~cut, color = "black", alpha = 0.3) %>%
  gf_facet_wrap(~cut, scales = "free_y", nrow = 2) %>%
  gf_labs(
    title = "Plot 3D: Prices Filled and Facetted by Cut",
    subtitle = "Free y-scale",
    caption = "ggformula"
  ) %>%
  gf_theme(theme(
    axis.text.x =
      element_text(
        angle = 45,
        hjust = 1
      )
  ))

# Set graph theme
theme_set(new = theme_custom())
#
diamonds %>% ggplot() +
  geom_histogram(aes(x = price, fill = cut), alpha = 0.3) +
  labs(title = "Plot 3A: Prices by Cut", caption = "ggplot")
##
diamonds %>%
  ggplot() +
  geom_histogram(aes(x = price, fill = cut),
    colour = "black", alpha = 0.3
  ) +
  labs(title = "Plot 3B: Prices filled by Cut", caption = "ggplot")
##
diamonds %>% ggplot() +
  geom_histogram(aes(price, fill = cut),
    colour = "black", alpha = 0.3
  ) +
  facet_wrap(facets = vars(cut)) +
  labs(
    title = "Plot 3C: Prices by Filled and Facetted by Cut",
    caption = "ggplot"
  ) +
  theme(axis.text.x = element_text(angle = 45, hjust = 1))
##
diamonds %>% ggplot() +
  geom_histogram(aes(price, fill = cut),
    colour = "black", alpha = 0.3
  ) +
  facet_wrap(facets = vars(cut), scales = "free_y") +
  labs(
    title = "Plot D: Prices by Filled and Facetted by Cut",
    subtitle = "Free y-scale",
    caption = "ggplot"
  ) +
  theme(axis.text.x = element_text(angle = 45, hjust = 1))

Business Insights-3

The price distribution is heavily skewed to the right AND This long-tailed nature of the histogram holds true regardless of the cut of the diamond.
See the x-axis range for each plot in Plot D! Price ranges are the same regardless of cut !! Very surprising! So cut is perhaps not the only thing that determines price…
Facetting the plot into small multiples helps look at patterns better: overlapping histograms are hard to decipher. Adding color defines the bars in the histogram very well.

A Hypothesis

The surprise insight above should lead you to make a Hypothesis! You should decide whether you want to investigate this question further, making more graphs, as we will see. Here, we are making a Hypothesis that more than just cut determines the price of a diamond.

An Interactive App for Histograms

Type in your Console:

```{r}
#| eval: false
install.packages("shiny")
library(shiny)
runExample("01_hello") # an interactive histogram
```

Case Study-2: `race` dataset

Import data

These data come from the TidyTuesday, project, a weekly social learning project dedicated to gaining practical experience with R and data science. In this case the TidyTuesday data are based on International Trail Running Association (ITRA) data but inspired by Benjamin Nowak. We will use the TidyTuesday data that are on GitHub. Nowak’s data are also available on GitHub.

race_df <- read_csv("https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2021/2021-10-26/race.csv")
rank_df <- read_csv("https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2021/2021-10-26/ultra_rankings.csv")

The data has automatically been read into the webr session, so you can continue on to the next code chunk!

Examine the race Data

Let us look at the dataset using all our three methods:

R
web-r

We will stick with just glimpse for this time, and not use skim or inspect in the interest of brevity:

glimpse(race_df)

Rows: 1,207
Columns: 13
$ race_year_id   <dbl> 68140, 72496, 69855, 67856, 70469, 66887, 67851, 68241,…
$ event          <chr> "Peak District Ultras", "UTMB®", "Grand Raid des Pyréné…
$ race           <chr> "Millstone 100", "UTMB®", "Ultra Tour 160", "PERSENK UL…
$ city           <chr> "Castleton", "Chamonix", "vielle-Aure", "Asenovgrad", "…
$ country        <chr> "United Kingdom", "France", "France", "Bulgaria", "Turk…
$ date           <date> 2021-09-03, 2021-08-27, 2021-08-20, 2021-08-20, 2021-0…
$ start_time     <time> 19:00:00, 17:00:00, 05:00:00, 18:00:00, 18:00:00, 17:0…
$ participation  <chr> "solo", "Solo", "solo", "solo", "solo", "solo", "solo",…
$ distance       <dbl> 166.9, 170.7, 167.0, 164.0, 159.9, 159.9, 163.8, 163.9,…
$ elevation_gain <dbl> 4520, 9930, 9980, 7490, 100, 9850, 5460, 4630, 6410, 31…
$ elevation_loss <dbl> -4520, -9930, -9980, -7500, -100, -9850, -5460, -4660, …
$ aid_stations   <dbl> 10, 11, 13, 13, 12, 15, 5, 8, 13, 23, 13, 5, 12, 15, 0,…
$ participants   <dbl> 150, 2300, 600, 150, 0, 300, 0, 200, 120, 100, 300, 50,…

glimpse(rank_df)

Rows: 137,803
Columns: 8
$ race_year_id    <dbl> 68140, 68140, 68140, 68140, 68140, 68140, 68140, 68140…
$ rank            <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, NA, NA, NA,…
$ runner          <chr> "VERHEUL Jasper", "MOULDING JON", "RICHARDSON Phill", …
$ time            <chr> "26H 35M 25S", "27H 0M 29S", "28H 49M 7S", "30H 53M 37…
$ age             <dbl> 30, 43, 38, 55, 48, 31, 55, 40, 47, 29, 48, 47, 52, 49…
$ gender          <chr> "M", "M", "M", "W", "W", "M", "W", "W", "M", "M", "M",…
$ nationality     <chr> "GBR", "GBR", "GBR", "GBR", "GBR", "GBR", "GBR", "GBR"…
$ time_in_seconds <dbl> 95725, 97229, 103747, 111217, 117981, 118000, 120601, …

We can also try our new friend mosaic::favstats:

race_df %>%
  favstats(~distance, data = .)

##
race_df %>%
  favstats(~participants, data = .)

##
rank_df %>%
  drop_na() %>%
  favstats(time_in_seconds ~ gender, data = .)

Introducing crosstable

mosaic::favstats allows to summarise just one variable at a time. On occasion we may need to see summaries of several Quant variables, over levels of Qual variables. This is where the package crosstable is so effective: note how crosstable also conveniently uses the formula interface that we are getting accustomed to.

We will find occasion to meet crosstable again when we do Inference.

## library(crosstable)
crosstable(time_in_seconds + age ~ gender, data = rank_df) %>%
  crosstable::as_flextable()

label	variable	gender
label	variable	M	W	NA
time_in_seconds	Min / Max	3600.0 / 2.9e+05	9191.0 / 3.0e+05	8131.0 / 2.2e+05
	Med [IQR]	1.2e+05 [9.7e+04;1.5e+05]	1.1e+05 [9.7e+04;1.3e+05]	1.2e+05 [9.9e+04;1.5e+05]
	Mean (std)	1.2e+05 (3.8e+04)	1.2e+05 (3.5e+04)	1.2e+05 (4.4e+04)
	N (NA)	101643 (15073)	18341 (2716)	28 (2)
age	Min / Max	0 / 133.0	0 / 81.0	29.0 / 59.0
	Med [IQR]	47.0 [40.0;53.0]	45.0 [39.0;52.0]	40.5 [36.0;50.5]
	Mean (std)	46.4 (10.2)	45.3 (9.7)	41.7 (9.0)
	N (NA)	116716 (0)	21057 (0)	30 (0)

(The as_flextable command from the crosstable package helped to render this elegant HTML table we see. It should be possible to do Word/PDF also, which we might see later.)

Business Insights from race data

We have two datasets, one for races (race_df) and one for the ranking of athletes (rank_df).
There is atleast one common column between the two, the race_year_id variable.
Overall, there are Qualitative variables such as country, city,gender, and participation. This last variables seems badly coded, with entries showing solo and Solo.
Quantitative variables are rank, time,time_in_seconds, age from rank_df; and distance, elevation_gain, elevation_loss,particants, and aid_stations from race_df.
We have 1207 races and over 130K participants! But some races do show zero participants!! Is that an error in data entry?

EDA with `race` datasets

Since this dataset is somewhat complex, we may for now just have a detailed set of Questions, that helps us get better acquainted with it. On the way, we may get surprised by some finding then want to go deeper, with a hunch or hypothesis.

Question-1: Max. Races and participants

Question #1

Which countries host the maximum number of races? Which countries send the maximum number of participants??

R
web-r

race_df %>%
  count(country) %>%
  arrange(desc(n))

rank_df %>%
  count(nationality) %>%
  arrange(desc(n))

The top three locations for races were the USA, UK, and France. These are also the countries that send the maximum number of participants, naturally!

Question-2: Max. Winners

Question #2

Which countries have the maximum number of winners (top 3 ranks)?

R
web-r

rank_df %>%
  filter(rank %in% c(1, 2, 3)) %>%
  count(nationality) %>%
  arrange(desc(n))

1240 Participants from the USA have been top 3 finishers. Across all races…

Question-3: Which countries have had the most top-3 finishes?

Question #3

Which countries have had the most top-3 finishes in the longest distance race?

Here we see we have ranks in one dataset, and race details in another! How do we do this now? We have to join the two data frames into one data frame, using a common variable that uniquely identifies observations in both datasets.

R
web-r

longest_races <- race_df %>%
  slice_max(n = 5, order_by = distance) # Longest distance races
longest_races
longest_races %>%
  left_join(., rank_df, by = "race_year_id") %>% # total participants in longest 4 races
  filter(rank %in% c(1:10)) %>% # Top 10 ranks
  count(nationality) %>%
  arrange(desc(n))

Wow….France has one the top 10 positions 26 times in the longest races… which take place in France, Thailand, Chad, Australia, and Portugal. So although the USA has the greatest number of top 10 finishes, when it comes to the longest races, it is 🇫🇷 vive la France!

Question-4: What is the distribution of the finishing times?

Question #4

What is the distribution of the finishing times, across all races and all ranks?

R
web-r

## Set graph theme
theme_set(new = theme_custom())
##

rank_df %>%
  gf_histogram(~time_in_seconds, bins = 75) %>%
  gf_labs(title = "Histogram of Race Times")

So the distribution is (very) roughly bell-shaped, spread over a 2X range. And some people may have dropped out of the race very early and hence we have a small bump close to zero time! The histogram shows three bumps…at least one reason is that the distances to be covered are not the same…but could there be other reasons? Like altitude_gained for example?

Question-5: What is the distribution of race distances?

Question #5

What is the distribution of race distances?

R
web-r

## Set graph theme
theme_set(new = theme_custom())
##

race_df %>%
  gf_histogram(~distance, bins = 50) %>%
  gf_labs(title = "Histogram of Race Distances")

Hmm…a closely clumped set of race distances, with some entries in between [0-150], but some are zero? Which are these?

race_df %>%
  filter(distance == 0)

Hmm…a closely clumped set of race distances, with some entries in between [0-150], but some are zero? Which are these?

Curious…some of these zero-distance races have had participants too! Perhaps these were cancelled events…all of them are stated to be 100 mile events…

Question-6: What is the distribution of finishing times for race distance around 150?

Question #6

For all races that have a distance around 150, what is the distribution of finishing times? Can these be split/facetted using start_time of the race (i.e. morning / evening) ?

R
web-r

Let’s make a count of start times:

race_times <- race_df %>%
  count(start_time) %>%
  arrange(desc(n))
race_times

Let’s convert start_time into a factor with levels: early_morning(0200:0600), late_morning(0600:1000), midday(1000:1400), afternoon(1400: 1800), evening(1800:2200), and night(2200:0200)

# Demo purposes only!

## Set graph theme
theme_set(new = theme_custom())
##

race_start_factor <- race_df %>%
  filter(distance == 0) %>% # Races that actually took place
  mutate(
    start_day_time =
      case_when(
        start_time > hms("02:00:00") &
          start_time <= hms("06:00:00") ~ "early_morning",
        start_time > hms("06:00:01") &
          start_time <= hms("10:00:00") ~ "late_morning",
        start_time > hms("10:00:01") &
          start_time <= hms("14:00:00") ~ "mid_day",
        start_time > hms("14:00:01") &
          start_time <= hms("18:00:00") ~ "afternoon",
        start_time > hms("18:00:01") &
          start_time <= hms("22:00:00") ~ "evening",
        start_time > hms("22:00:01") &
          start_time <= hms("23:59:59") ~ "night",
        start_time >= hms("00:00:00") &
          start_time <= hms("02:00:00") ~ "postmidnight",
        .default = "other"
      )
  ) %>%
  mutate(
    start_day_time =
      as_factor(start_day_time) %>%
        fct_collapse(
          .f = .,
          night = c("night", "postmidnight")
        )
  )
##
# Join with rank_df
race_start_factor %>%
  left_join(rank_df, by = "race_year_id") %>%
  drop_na(time_in_seconds) %>%
  gf_histogram(
    ~time_in_seconds,
    bins = 75,
    fill = ~start_day_time,
    color = ~start_day_time,
    alpha = 0.5
  ) %>%
  gf_facet_wrap(vars(start_day_time), ncol = 2, scales = "free_y") %>%
  gf_labs(title = "Race Times by Start-Time")

Let’s make a count of start times:

Let’s convert start_time into a factor with levels: early_morning(0200:0600), late_morning(0600:1000), midday(1000:1400), afternoon(1400: 1800), evening(1800:2200), and night(2200:0200)

We see that finish times tend to be longer for afternoon and evening start races; these are lower for early morning and night time starts. Mid-day starts show a curious double hump in finish times that should be studied.

Distributions and Densities in the Wild

Before we conclude, let us look at a real world dataset: populations of countries. This dataset was taken from Kaggle https://www.kaggle.com/datasets/ulrikthygepedersen/populations. Click on the icon below to save the file into a subfolder called data in your project folder:

pop <- read_csv("data/populations.csv")
pop
inspect(pop)


categorical variables:  
          name     class levels     n missing
1 country_code character    265 16400       0
2 country_name character    265 16400       0
                                   distribution
1 ABW (0.4%), AFE (0.4%), AFG (0.4%) ...       
2 Afghanistan (0.4%) ...                       

quantitative variables:  
   name   class  min       Q1  median       Q3        max         mean
1  year numeric 1960   1975.0    1991     2006       2021 1.990529e+03
2 value numeric 2646 986302.5 6731400 46024452 7888408686 2.140804e+08
            sd     n missing
1 1.789551e+01 16400       0
2 7.040554e+08 16400       0

Let us plot densities/histograms for value:

## Set graph theme
theme_set(new = theme_custom())
##

##
gf_histogram(~value, data = pop, title = "Long Tailed Histogram")
##
gf_density(~value, data = pop, title = "Long Tailed Density")

These graphs convey very little to us: the data is very heavily skewed to the right and much of the chart is empty. There are many countries with small populations and a few countries with very large populations. Such distributions are also called “long tailed” distributions. To develop better insights with this data, we should transform the variable concerned, using say a “log” transformation:

## Set graph theme
theme_set(new = theme_custom())
##

gf_histogram(~ log10(value), data = pop, title = "Histogram with Log transformed x-variable")
##
gf_density(~ log10(value), data = pop, title = "Density with Log transformed x-variable")

Be prepared to transform your data with log or sqrt transformations when you see skewed distributions!

Pareto, Power Laws, and Fat Tailed Distributions

City Populations, Sales across product categories, Salaries, Instagram connections, number of customers vs Companies, net worth / valuation of Companies, extreme events on stock markets….all of these could have highly skewed distributions. In such a case, the standard statistics of mean/median/sd may not convey too much information. With such distributions, one additional observation on say net worth, like say Mr Gates’, will change these measures completely. (More when we discuss Sampling)

Since very large observations are indeed possible, if not highly probable, one needs to look at the result of such an observation and its impact on a situation rather than its (mere) probability. Classical statistical measures and analysis cannot apply with long-tailed distributions. More on this later in the Module on Statistical Inference, but for now, here is a video that talks in detail about fat-tailed distributions, and how one should use them and get used to them:

Several distribution shapes exist, here is an illustration of the 6 most common ones:

What insights could you develop based on these distribution shapes?

Bimodal: Maybe two different systems or phenomena or regimes under which the data unfolds. Like our geyser above. Or a machine that works differently when cold and when hot. Intermittent faulty behaviour…
Comb: Some specific Observations occur predominantly, in an otherwise even spread or observations. In a survey many respondents round off numbers to nearest 100 or 1000. Check the distribution of the diamonds dataset for carat values which are suspiciously integer numbers in too many cases.
Edge Peak: Could even be a data entry artifact!! All unknown / unrecorded observations are recorded as $999$ !!🙀
Normal: Just what it says! Course Marks in a Univ cohort…
Skewed: Income, or friends count in a set of people. Do UI/UX peasants have more followers on Insta than say CAP people?
Uniform: The World is ~~not~~ flat. Anything can happen within a range. But not much happens outside! Sharp limits…

Z-scores

Often when we compute wish to compare distributions with different values for means and standard deviations, we resort to a scaling of the variables that are plotted in the respective distributions.

[1] 0.9772499

[1] 0.7475075

Although the densities all look the same, they are are quite different! The x-axis in each case has two scales: one is the actual value of the x-variable, and the other is the z-score which is calculated as:

\[ z_x = \frac{x - \mu_{x}}{\sigma_x} \]

With similar distributions (i.e. normal distributions), we see that the variation in density is the same at the same values of z-score for each variable. However since the $\mu_i$ and $\sigma_i$ are different, the absolute value of the z-score is different for each variable. In the first plot (from the top left), $z = 1$ corresponds to an absolute change of $5$ units; it is $15$ units in the plot directly below it.

Our comparisons are done easily when we compare differences in probabilities at identical z-scores, or differences in z-scores at identical probabilities.

Wait, But Why?

Histograms are used to study the distribution of one or a few Quant variables.
Checking the distribution of your variables one by one is probably the first task you should do when you get a new dataset.
It delivers a good quantity of information about spread, how frequent the observations are, and if there are some outlandish ones.
Comparing histograms side-by-side helps to provide insight about whether a Quant measurement varies with situation (a Qual variable). We will see this properly in a statistical way soon.

Conclusion

To complicate matters: Having said all that, the histogram is really a bar chart in disguise! You probably suspect that the “bucketing” of the Quant variable is tantamount to creating a Qual variable! Each bucket is a level in this fictitious bucketed Quant variable.

Histograms, Frequency Distributions, and Box Plots are used for Quantitative data variables
Histograms “dwell upon” counts, ranges, means and standard deviations
We can split histograms on the basis of another Qualitative variable.
Long tailed distributions need care in visualization and in inference making!

Your Turn

Old Faithful Data in R (Find it!)

2. Wage and Education Data from Canada

3. Time taken to Open or Close Packages

Some students/HCD peasants tested Elderly people, some with and some without hand pain, and observed how long they took to open or close typical packages for milk, cheese, bottles etc.

inspect the dataset in each case and develop a set of Questions, that can be answered by appropriate stat measures, or by using a chart to show the distribution.

Tip

Note: reading xlsx files into R may need the the readxl package. Install it!!

AI Generated Summary and Podcast

This module is an excerpt from a guide on learning statistical analysis using metaphors. The text focuses on the concept of quantitative variables and how histograms can be used to visualize their distribution. The author illustrates these concepts through real-world examples using datasets such as diamond prices, ultramarathon race times, and global population figures. By analyzing these datasets with histograms, the author explores various aspects of data distributions, including skewness, bimodality, and the presence of outliers. The guide also introduces additional tools like the crosstable package and z-scores to enhance data analysis. Finally, the author encourages readers to apply these concepts to real-world datasets, developing questions and insights through the use of histograms and statistical measures.

What patterns emerge from the distributions of quantitative variables in each dataset, and what insights can we gain about the relationships between these variables?
How do different qualitative variables impact the distribution of quantitative variables in the datasets, and what are the implications of these findings for understanding the underlying phenomena?
Based on the distributions and relationships between variables, what are the most relevant questions to ask about the datasets, and what further analyses could be conducted

References

See the scrolly animation for a histogram at this website: Exploring Histograms, an essay by Aran Lunzer and Amelia McNamara https://tinlizzie.org/histograms/?s=09
Minimal R using mosaic.https://cran.r-project.org/web/packages/mosaic/vignettes/MinimalRgg.pdf
Sebastian Sauer, Plotting multiple plots using purrr::map and ggplot

R Package Citations

Package	Version	Citation
crosstable	0.8.0	Chaltiel (2024)
ggridges	0.5.6	Wilke (2024)
NHANES	2.1.0	Pruim (2015)
TeachHist	0.2.1	Lange (2023)
TeachingDemos	2.13	Snow (2024)
visualize	4.5.0	Balamuta (2023)

Balamuta, James. 2023. visualize: Graph Probability Distributions with User Supplied Parameters and Statistics. https://CRAN.R-project.org/package=visualize.

Chaltiel, Dan. 2024. crosstable: Crosstables for Descriptive Analyses. https://CRAN.R-project.org/package=crosstable.

Lange, Carsten. 2023. TeachHist: A Collection of Amended Histograms Designed for Teaching Statistics. https://CRAN.R-project.org/package=TeachHist.

Pruim, Randall. 2015. NHANES: Data from the US National Health and Nutrition Examination Study. https://CRAN.R-project.org/package=NHANES.

Snow, Greg. 2024. TeachingDemos: Demonstrations for Teaching and Learning. https://CRAN.R-project.org/package=TeachingDemos.

Wilke, Claus O. 2024. ggridges: Ridgeline Plots in “ggplot2”. https://CRAN.R-project.org/package=ggridges.

Citation

BibTeX citation:

@online{v.2022,
  author = {V., Arvind},
  title = {\textless Iconify-Icon Icon=“fluent-Mdl2:quantity”
    Width=“1.2em”
    Height=“1.2em”\textgreater\textless/Iconify-Icon\textgreater{}
    {Quantities}},
  date = {2022-11-15},
  url = {https://av-quarto.netlify.app/content/courses/Analytics/Descriptive/Modules/22-Histograms/},
  langid = {en},
  abstract = {Quant and Qual Variable Graphs and their Siblings}
}

For attribution, please cite this work as:

V., Arvind. 2022. “<Iconify-Icon Icon=‘fluent-Mdl2:quantity’ Width=‘1.2em’ Height=‘1.2em’></Iconify-Icon> Quantities.” November 15, 2022. https://av-quarto.netlify.app/content/courses/Analytics/Descriptive/Modules/22-Histograms/.

Slides and Tutorials

Setting up R Packages

What graphs will we see today?

What kind of Data Variables will we choose?

Inspiration

How do Histograms Work?

Case Study-1: diamonds dataset

Examine the Data

Data Dictionary

Hypothesis and Research Questions

Plotting Histograms

Question-1: What is the distribution of the target variable price?

Business Insights-1

Question-2: What is the distribution of the predictor variable carat?

Business Insights-2

Question-3: Does a price distribution vary based upon type of cut, clarity, and color?

Business Insights-3

An Interactive App for Histograms

Case Study-2: race dataset

Import data

Examine the race Data

EDA with race datasets

Question-1: Max. Races and participants

Question-2: Max. Winners

Question-3: Which countries have had the most top-3 finishes?

Question-4: What is the distribution of the finishing times?

Question-5: What is the distribution of race distances?

Question-6: What is the distribution of finishing times for race distance around 150?

Distributions and Densities in the Wild

Pareto, Power Laws, and Fat Tailed Distributions

Z-scores

Wait, But Why?

Conclusion

Your Turn

AI Generated Summary and Podcast

References

R Package Citations

Citation

Case Study-1: `diamonds` dataset

Question-1: What is the distribution of the target variable `price`?

Question-2: What is the distribution of the predictor variable `carat`?

Question-3: Does a `price` distribution vary based upon type of `cut`, `clarity`, and `color`?

Case Study-2: `race` dataset

EDA with `race` datasets