🃏 Inference for a Single Mean

“The more I love humanity in general, the less I love man in particular. ― Fyodor Dostoyevsky, The Brothers Karamazov

t.test
Inference
Bootstrap
Null Distributions
Generating Parallel Worlds
Author

Arvind V.

Published

November 10, 2022

Modified

October 18, 2024

Abstract
Inference Tests for a Single population Mean

…neither let us despair over how small our successes are. For however much our successes fall short of our desire, our efforts aren’t in vain when we are farther along today than yesterday.

— John Calvin

Setting up R packages

library(tidyverse)
library(mosaic)
library(ggformula)
library(infer)
library(broom) # Clean test results in tibble form
library(resampledata) # Datasets from Chihara and Hesterberg's book
library(openintro) # More datasets

Plot Theme

Show the Code
# https://stackoverflow.com/questions/74491138/ggplot-custom-fonts-not-working-in-quarto

# Chunk options
knitr::opts_chunk$set(
  fig.width = 7,
  fig.asp = 0.618, # Golden Ratio
  # out.width = "80%",
  fig.align = "center", tidy = TRUE
)
### Ggplot Theme
### https://rpubs.com/mclaire19/ggplot2-custom-themes

theme_custom <- function() {
  font <- "Roboto Condensed" # assign font family up front

  theme_classic(base_size = 14) %+replace% # replace elements we want to change

    theme(
      text = element_text(family = font),
      panel.grid.minor = element_blank(), # strip minor gridlines

      # text elements
      plot.title = element_text( # title
        family = font, # set font family
        # size = 20,               #set font size
        face = "bold", # bold typeface
        hjust = 0, # left align
        # vjust = 2                #raise slightly
        margin = margin(0, 0, 10, 0)
      ),
      plot.subtitle = element_text( # subtitle
        family = font, # font family
        # size = 14,                #font size
        hjust = 0,
        margin = margin(2, 0, 5, 0)
      ),
      plot.caption = element_text( # caption
        family = font, # font family
        size = 8, # font size
        hjust = 1
      ), # right align

      axis.title = element_text( # axis titles
        family = font, # font family
        size = 10 # font size
      ),
      axis.text = element_text( # axis text
        family = font, # axis family
        size = 8
      ) # font size
    )
}

# Set graph theme
theme_set(new = theme_custom())
#

Introduction

In this module, we will answer a basic Question: What is the mean \(\mu\) of the population?

Recall that the mean is the first of our Summary Statistics. We wish to know more about the mean of the population from which we have drawn our data sample.

We will do this is in several ways, based on the assumptions we are willing to adopt about our data. First we will use a toy dataset with one “imaginary” sample, normally distributed and made up of 50 observations. Since we “know the answer” we will be able to build up some belief in the tests and procedures, which we will dig into to form our intuitions.

We will then use a real-world dataset to make inferences on the means of Quant variables therein, and decide what that could tell us.

Statistical Inference is almost an Attitude!

As we will notice, the process of Statistical Inference is an attitude: ain’t nothing happenin’! We look at data that we might have received or collected ourselves, and look at it with this attitude, seemingly, of some disbelief. We state either that:

  1. there is really nothing happening with our research question, and that anything we see in the data is the outcome of random chance.
  2. the value/statistic indicated by the data is off the mark and ought to be something else.

We then calculate how slim the chances are of the given data sample showing up like that, given our belief. It is a distance measurement of sorts. If those chances are too low, then that might alter our belief. This is the attitude that lies at the heart of Hypothesis Testing.

Important

The calculation of chances is both a logical, and a possible procedure since we are dealing with samples from a population. If many other samples give us quite different estimates, then we would discredit the one we derive from it.

Each test we perform will mechanize this attitude in different ways, based on assumptions and conveniences. (And history)

Case Study #1: Toy data

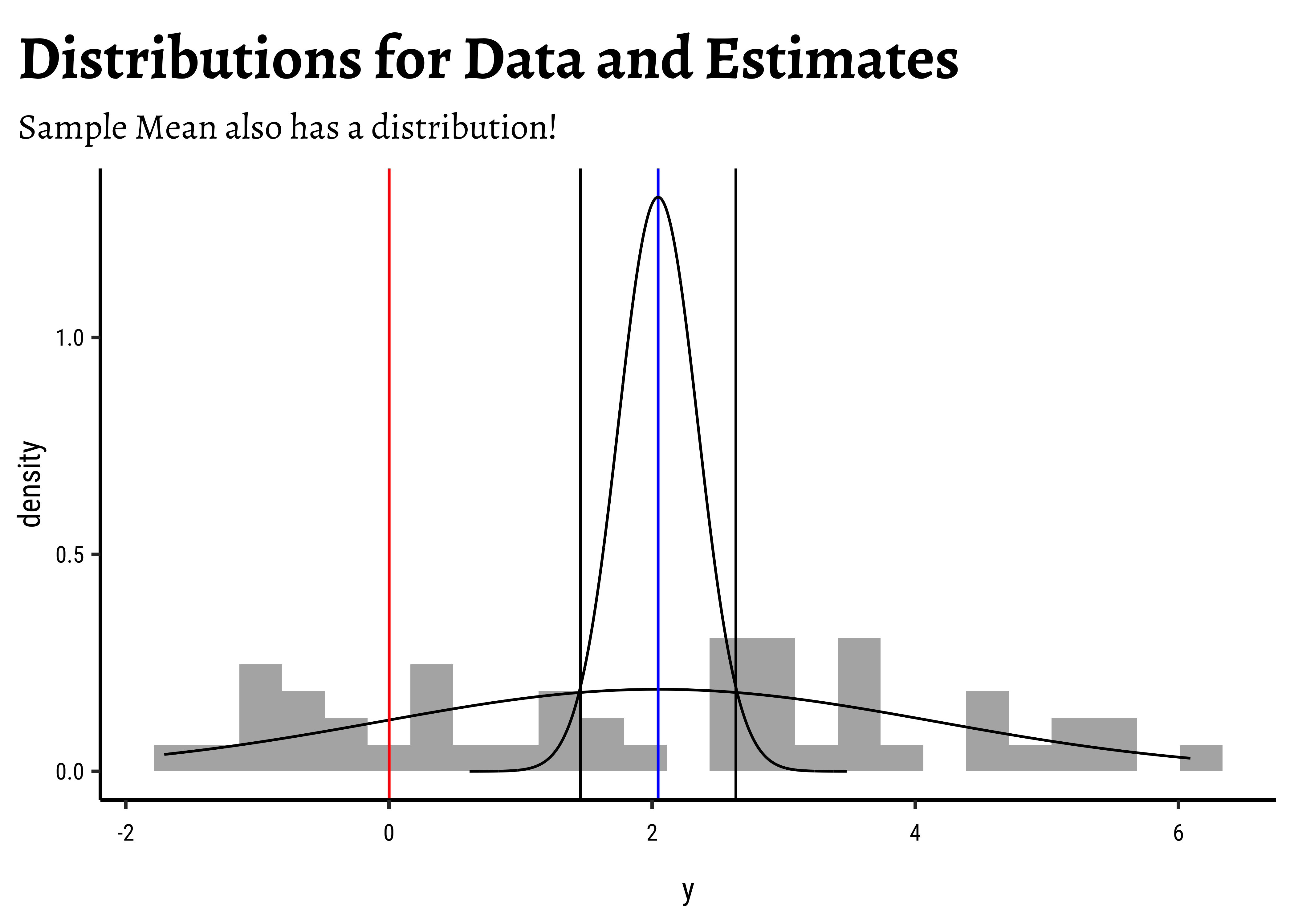
Since the CLT assumes the sample is normally-distributed, let us generate a sample that is just so:

set.seed(40) # for replication
#
# Data as individual vectors
# ( for t.tests etc)
# Generate normally distributed data with mean = 2, sd = 2, length = 50
y <- rnorm(n = 50, mean = 2, sd = 2)

# And as tibble too
mydata <- tibble(y = y)
mydata

Inspecting and Charting Data

# Set graph theme
theme_set(new = theme_custom())
#
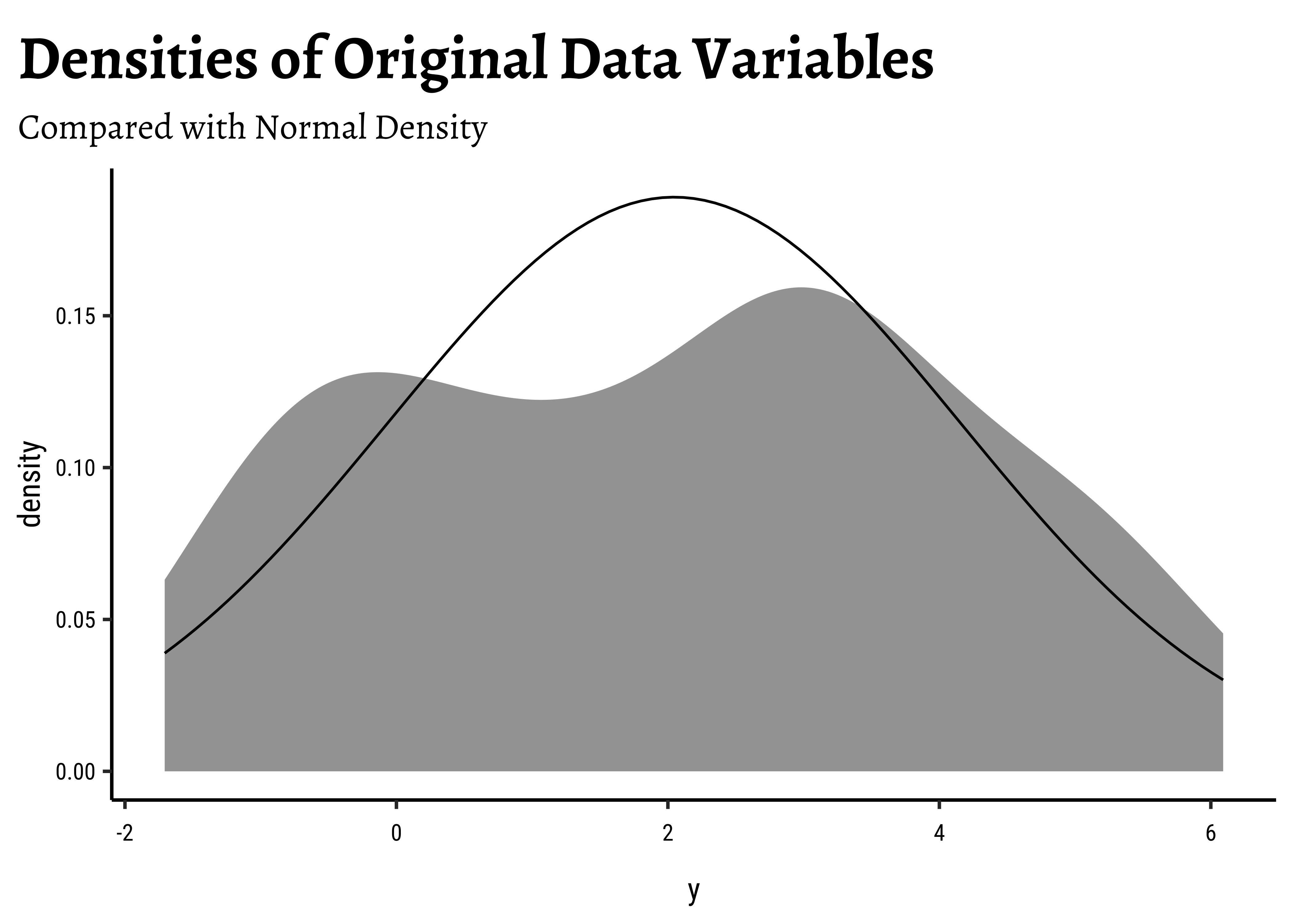
mydata %>%
  gf_density(~y) %>%
  gf_fitdistr(dist = "dnorm") %>%
  gf_labs(
    title = "Densities of Original Data Variables",
    subtitle = "Compared with Normal Density"
  )

Observations from Density Plots
  • The variable \(y\) appear to be centred around
  • It does not seem to be normally distributed…
  • So assumptions are not always valid…

Research Question

Research Questions are always about the population! Here goes:

Research Question

Could the mean of the population \(\mu\), from which y has been drawn, be zero?

Assumptions

Testing for Normality

The y-variable does not appear to be normally distributed. This would affect the test we can use to make inferences about the population mean.
There are formal tests for normality too. We will do them in the next case study. For now, let us proceed naively.

Inference

A. Model

We have \(mean(y) = \bar{y}.\) We formulate “our disbelief” of \(\bar{y}\) with a NULL Hypothesis, about the population as follows:

\[ \ H_0: \mu = 0 \] And the alternative hypothesis, again about the population as

\[ H_a:\mu \ne 0 \]

B. Code

# t-test
t1 <- mosaic::t_test(
  y, # Name of variable
  mu = 0, # belief of population mean
  alternative = "two.sided"
) %>% # Check both sides

  broom::tidy() # Make results presentable, and plottable!!
t1
Recall Confidence Intervals

Recall how we calculated means, standard deviations from data (samples). If we could measure the entire population, then there would be no uncertainty in our estimates for means and sd-s. Since we are forced to sample, we can only estimate population parameters based on the sample estimates and state how much off we might be.

Confidence intervals for population means are given by:

\[ \begin{eqnarray*} CI & = & \bar{y} ~ {\pm ~ constant * Standard Error}\\ & = & \bar{y} ~ {\pm ~ 1.96 * {sd/\sqrt{n}}} \end{eqnarray*} \]

Assuming the y is normally-distributed, the \(constant = 1.96\) for confidence level of 95%. What that means is that if we take multiple such samples like \(y\) from the population, their means (which are random) will land within \(CI\) of the population mean (which is fixed!) 95% of the time. Uff…! May remind you of Buffon’s Needle…

So \(\bar{y}\) i.e. the estimate is \(2.045689\). The confidence intervals do not straddle zero. The chances that this particular value of mean (\(2.045689\)) would randomly occur under the assumption that \(\mu\) is zero, are exceedingly slim, \(p.value = 1.425495e-08\). Hence we can reject the NULL hypothesis that the true population, of which y is a sample, could have mean \(\mu = 0\).

“Signed Rank” Values: A Small Digression

When the Quant variable we want to test for is not normally distributed, we need to think of other ways to perform our inference. Our assumption about normality has been invalidated.
Most statistical tests use the actual values of the data variables. However, in these cases where assumptions are invalidated, the data are used in rank-transformed sense/order. In some cases the signed-rank of the data values is used instead of the data itself. The signed ranks are then tested to see if there are more of one polarity than the other, roughly speaking, and how probable this could be.

Signed Rank is calculated as follows:

  1. Take the absolute value of each observation in a sample
  2. Place the ranks in order of (absolute magnitude). The smallest number has rank = 1 and so on.
  3. Give each of the ranks the sign of the original observation ( + or -)
signed_rank <- function(x) {
  sign(x) * rank(abs(x))
}

Since we are dealing with the mean, the sign of the rank becomes important to use.

A. Model

\[ mean(signed\_rank(y)) = \beta_0 \]

\[ H_0: \mu_0 = 0 \] \[ H_a: \mu_0 \ne 0 \]

B. Code

# Standard Wilcoxon Signed_Rank Test
t2 <- wilcox.test(y, # variable name
  mu = 0, # belief
  alternative = "two.sided",
  conf.int = TRUE,
  conf.level = 0.95
) %>%
  broom::tidy()
t2
# Can also do this equivalently
# t-test with signed_rank data
t3 <- t.test(signed_rank(y),
  mu = 0,
  alternative = "two.sided",
  conf.int = TRUE,
  conf.level = 0.95
) %>%
  broom::tidy()
t3

Again, the confidence intervals do not straddle \(0\), and we need to reject the belief that the mean is close to zero.

Note

Note how the Wilcoxon Test reports results about \(y\), even though it computes with \(signed-rank(y)\). The “equivalent t-test” with signed-rank data cannot do this, since it uses “rank” data, and reports the same result.

We saw from the diagram created by Allen Downey that there is only one test 1! We will now use this philosophy to develop a technique that allows us to mechanize several Statistical Models in that way, with nearly identical code.

We can use two packages in R, mosaic to develop our intuition for what are called permutation based statistical tests; and a more recent package called infer in R which can do pretty much all of this, including visualization.

We will stick with mosaic for now. We will do a permutation test first, and then a bootstrap test. In subsequent modules, we will use infer also.

For the Permutation test, we mechanize our belief that \(\mu = 0\) by shuffling the polarities of the y observations randomly 4999 times to generate other samples from the population \(y\) could have come from2. If these samples can frequently achieve \(\bar{y_i} \leq 0\), then we might believe that the population mean may be 0!

We see that the means here that chances that the randomly generated means can exceed our real-world mean are about \(0\)! So the mean is definitely different from \(0\).

# Set graph theme
theme_set(new = theme_custom())
#
# Calculate exact mean
obs_mean <- mean(~y, data = mydata)
belief1 <- 0 # What we think the mean is
obs_diff_mosaic <- obs_mean - belief1
obs_diff_mosaic
[1] 2.045689
## Steps in Permutation Test
## Repeatedly Shuffle polarities of data observations
## Take means
## Compare all means with the real-world observed one
null_dist_mosaic <-
  mosaic::do(9999) * mean(
    ~ abs(y) *
      sample(c(-1, 1), # +/- 1s multiply y
        length(y), # How many +/- 1s?
        replace = T
      ), # select with replacement
    data = mydata
  )
##
range(null_dist_mosaic$mean)
[1] -1.754293  1.473298
##
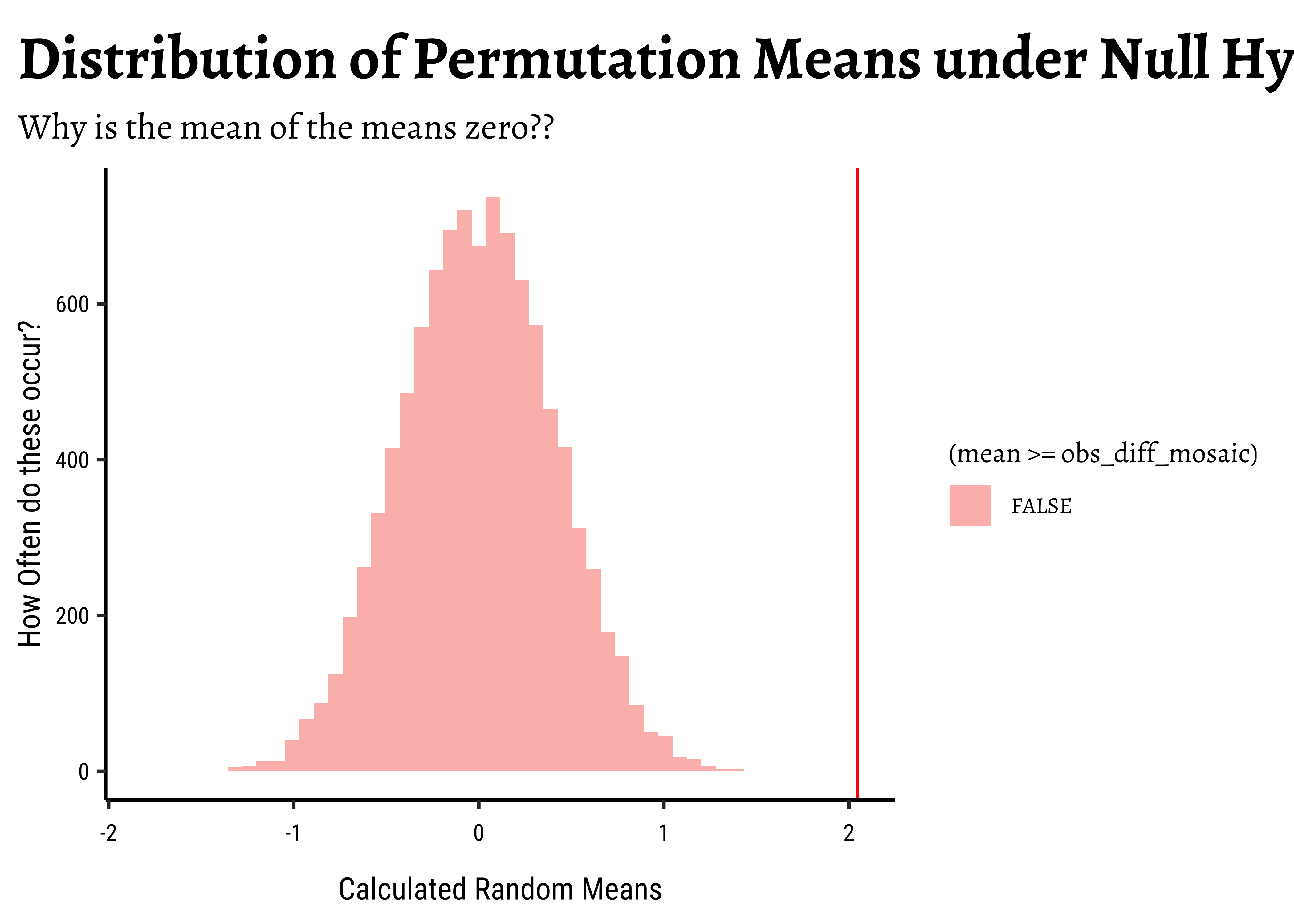
## Plot this NULL distribution
gf_histogram(
  ~mean,
  data = null_dist_mosaic,
  fill = ~ (mean >= obs_diff_mosaic),
  bins = 50, title = "Distribution of Permutation Means under Null Hypothesis",
  subtitle = "Why is the mean of the means zero??"
) %>%
  gf_labs(
    x = "Calculated Random Means",
    y = "How Often do these occur?"
  ) %>%
  gf_vline(xintercept = obs_diff_mosaic, colour = "red")

# p-value
# Null distributions are always centered around zero. Why?
prop(~ mean >= obs_diff_mosaic,
  data = null_dist_mosaic
)
prop_TRUE 
        0

Let us try the bootstrap test now: Here we simulate samples, similar to the one at hand, using repeated sampling the sample itself, with replacement, a process known as bootstrapping, or bootstrap sampling.

# Set graph theme
theme_set(new = theme_custom())
##
## Resample with replacement from the one sample of 50
## Calculate the mean each time
null_toy_bs <- mosaic::do(4999) *
  mean(
    ~ sample(y,
      replace = T
    ), # select with replacement
    data = mydata
  )

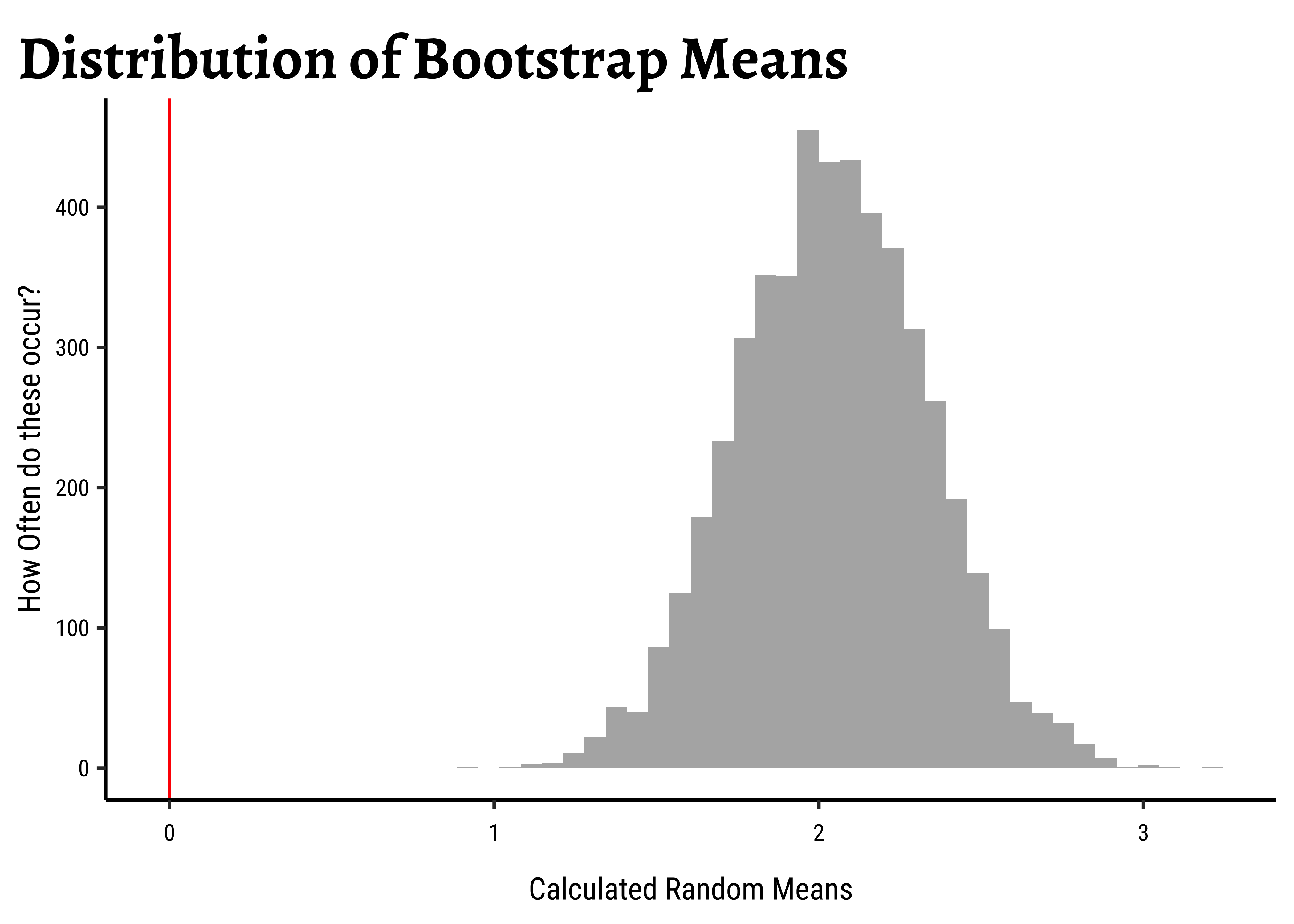
## Plot this NULL distribution
gf_histogram(
  ~mean,
  data = null_toy_bs,
  bins = 50,
  title = "Distribution of Bootstrap Means"
) %>%
  gf_labs(
    x = "Calculated Random Means",
    y = "How Often do these occur?"
  ) %>%
  gf_vline(xintercept = ~belief1, colour = "red")

prop(~ mean >= belief1,
  data = null_toy_bs
) +
  prop(~ mean <= -belief1,
    data = null_toy_bs
  )
prop_TRUE 
        1
Permutation vs Bootstrap

There is a difference between the two. The bootstrap test uses the sample at hand to generate many similar samples without access to the population, and calculates the statistic needed (i.e. mean). No Hypothesis is stated. The distribution of bootstrap samples looks “similar” to that we might obtain by repeatedly sampling the population itself. (centred around a population parameter, i.e. \(\mu\))

The permutation test generates many permutations of the data and generates appropriates measures/statistics under the NULL hypothesis. Which is why the permutation test has a NULL distribution centered at \(0\) in this case, our NULL hypothesis.

As student Sneha Manu Jacob remarked in class, Permutation flips the signs of the data values in our sample; Bootstrap flips the number of times each data value is (re)used. Good Insight!!

Yes, the t-test works, but what is really happening under the hood of the t-test? The inner mechanism of the t-test can be stated in the following steps:

  1. Calculate the mean of the sample \(\bar{y}\).
  2. Calculate the sd of the sample, and, assuming the sample is normally distributed, calculate the standard error (i.e. \(\frac{sd}{\sqrt{n}}\))
  3. Take the difference between the sample mean \(\bar{y}\) and our expected/believed population mean \(\mu\).
  4. We expect that the population mean ought to be within the confidence interval of the sample mean \(\bar{y}\).
  5. For a normally distributed sample, the confidence interval is given by \(\pm1.96 * standarderror\), to be 95% sure that the sample mean is a good estimate for the population mean.
  6. Therefore if the difference between actual and believed is far beyond the confidence interval, hmm…we cannot think our belief is correct and we change our opinion.

Let us translate that mouthful into calculations!

mean_belief_pop <- 0.0 # Assert our belief
# Sample Mean
mean_y <- mean(y)
mean_y
[1] 2.045689
## Sample standard error
std_error <- sd(y) / sqrt(length(y))
std_error
[1] 0.3014752
## Confidence Interval of Observed Mean
conf_int <- tibble(ci_low = mean_y - 1.96 * std_error, ci_high = mean_y + 1.96 * std_error)
conf_int
## Difference between actual and believed mean
mean_diff <- mean_y - mean_belief_pop
mean_diff
[1] 2.045689
## Test Statistic
t <- mean_diff / std_error
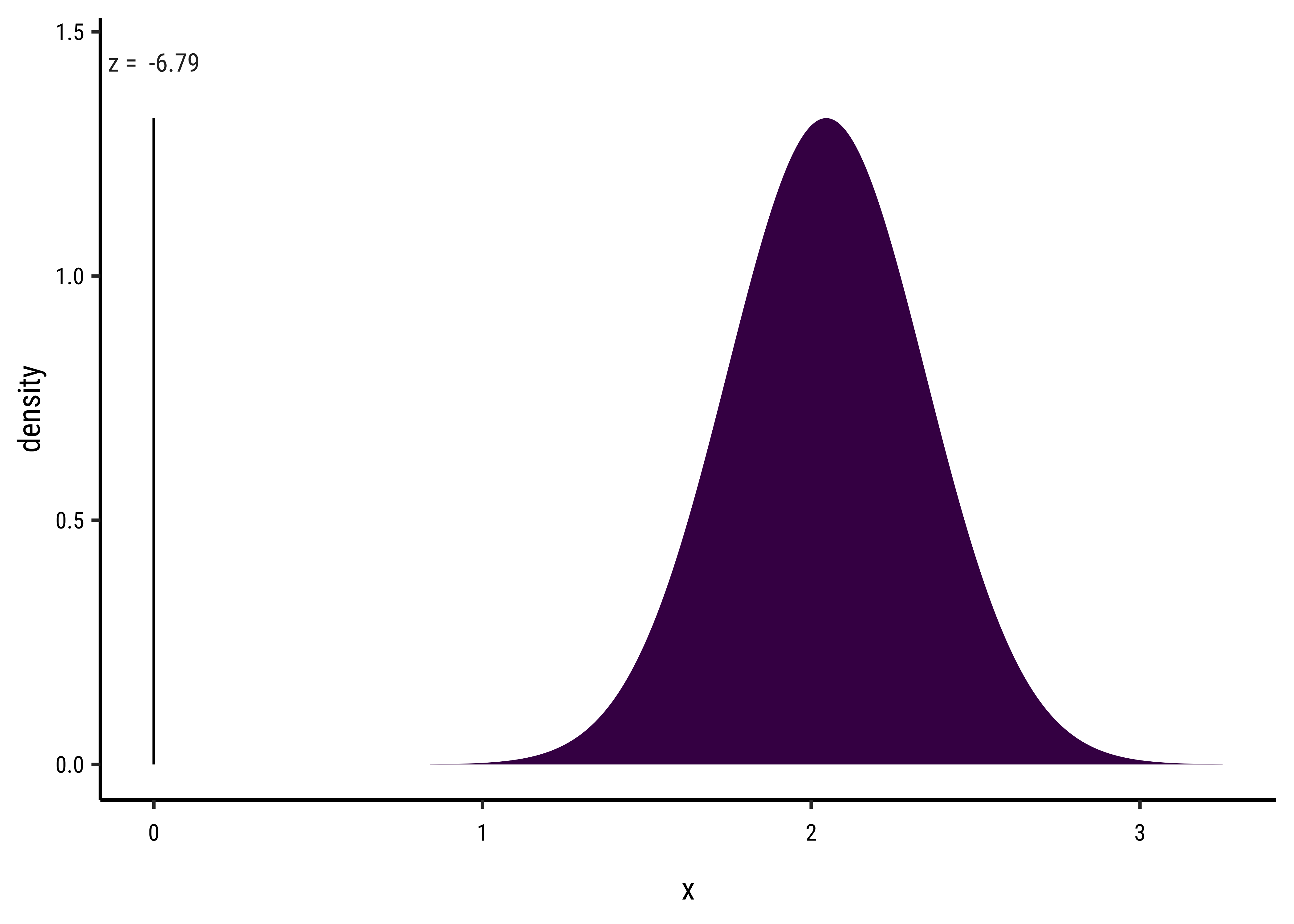
t
[1] 6.785596

We see that the difference between means is 6.78 times the std_error! At a distance of 1.96 (either way) the probability of this data happening by chance already drops to 5%!! At this distance of 6.78, we would have negligible probability of this data occurring by chance!

How can we visualize this?

If X ~ N(2.046, 0.3015), then 
    P(X <= 1.443e-07) = P(Z <= -6.786) = 5.78e-12
    P(X >  1.443e-07) = P(Z >  -6.786) = 1

[1] 5.780412e-12

Case Study #2: Exam data

Let us now choose a dataset from the openintro package:

data("exam_grades")
exam_grades

Research Question

There are quite a few Quant variables in the data. Let us choose course_grade as our variable of interest. What might we wish to find out?

Research Question

In general, the Teacher in this class is overly generous with grades unlike others we know of, and so the average course-grade is equal to 80% !!

Inspecting and Charting Data

# Set graph theme
theme_set(new = theme_custom())
#
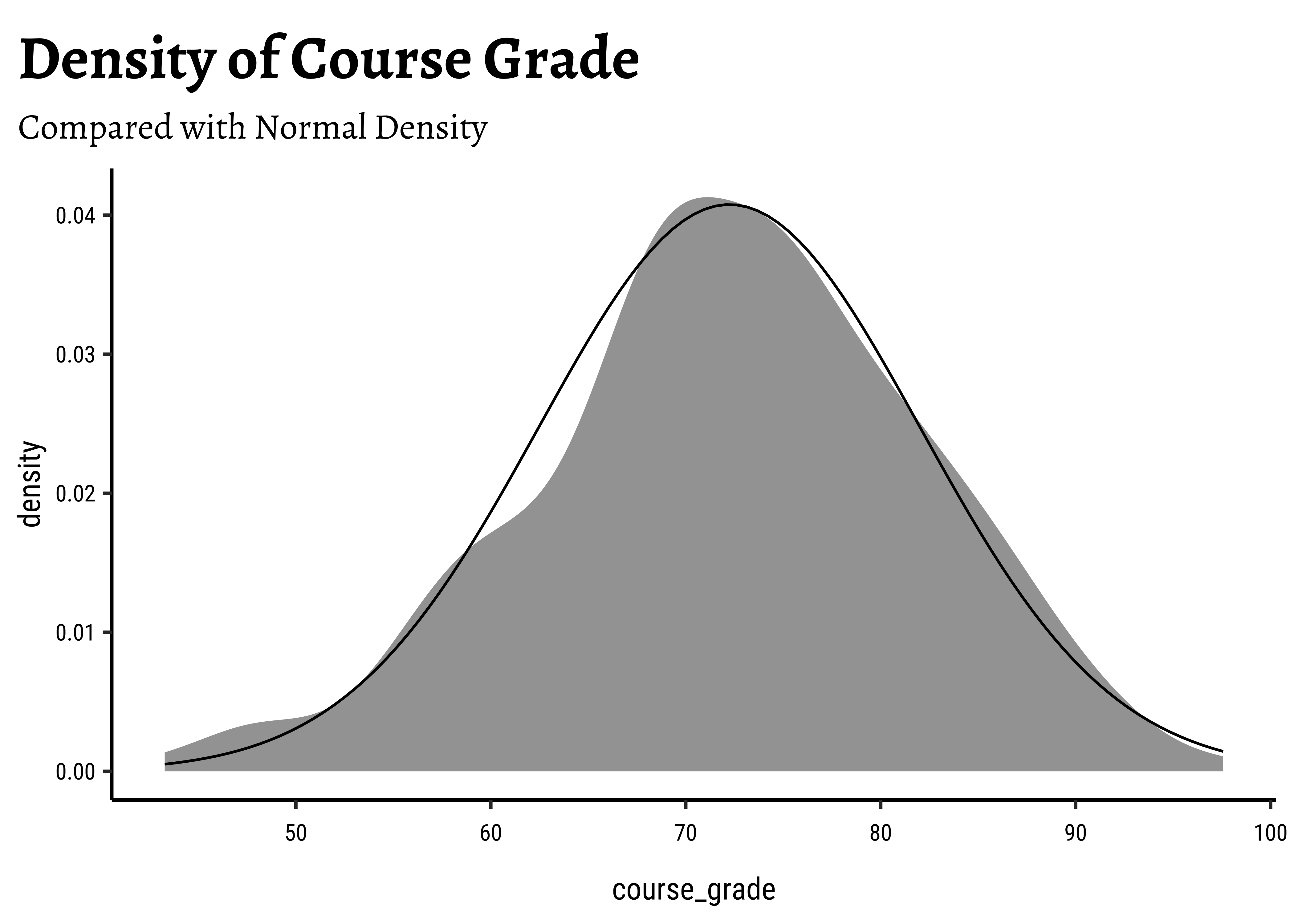
exam_grades %>%
  gf_density(~course_grade) %>%
  gf_fitdistr(dist = "dnorm") %>%
  gf_labs(
    title = "Density of Course Grade",
    subtitle = "Compared with Normal Density"
  )

Hmm…data looks normally distributed. But this time we will not merely trust our eyes, but do a test for it.

Testing Assumptions in the Data

Is the data normally distributed? 
stats::shapiro.test(x = exam_grades$course_grade) %>%
  broom::tidy()

The Shapiro-Wilkes Test tests whether a data variable is normally distributed or not. Without digging into the maths of it, let us say it makes the assumption that the variable is so distributed and then computes the probability of how likely this is. So a high p-value (\(0.47\)) is a good thing here.

When we have large Quant variables ( i.e. with length >= 5000), the shapiro.test does not work, and we use an Anderson-Darling3 test to confirm normality:

library(nortest)
# Especially when we have >= 5000 observations
nortest::ad.test(x = exam_grades$course_grade) %>%
  broom::tidy()

So course_grade is a normally-distributed variable. There are no exceptional students! Hmph!

Inference

A. Model

We have that \(mean(course\_grade) = \beta_0\). As before, we formulate “our (dis)belief” in this sample mean with a NULL Hypothesis about the population, as follows:

\[ \ H_0: \mu= 80 \]

\[ H_a: \mu \ne 80 \]

B. Code

# t-test
t4 <- mosaic::t_test(
  exam_grades$course_grade, # Name of variable
  mu = 80, # belief
  alternative = "two.sided"
) %>% # Check both sides
  broom::tidy()
t4

So, we can reject the NULL Hypothesis that the average grade in the population of students who have taken this class is 80, since there is a minuscule chance that we would see an observed sample mean of 72.238, if the population mean \(\mu\) had really been \(80\).

# t-test
t5 <- wilcox.test(
  exam_grades$course_grade, # Name of variable
  mu = 90, # belief
  alternative = "two.sided",
  conf.int = TRUE,
  conf.level = 0.95
) %>% # Check both sides

  broom::tidy() # Make results presentable, and plottable!!
t5

This test too suggests that the average course grade is different from 80.

Why compare on both sides?

Note that we have computed whether the average course_grade is generally different from 80 for this Teacher. We could have computed whether it is greater, or lesser than 80 ( or any other number too). Read this article for why it is better to do a “two.sided” test in most cases.

# Set graph theme
theme_set(new = theme_custom())
#
# Calculate exact mean
obs_mean_grade <- mean(~course_grade, data = exam_grades)
belief <- 80
obs_grade_diff <- belief - obs_mean_grade
## Steps in a Permutation Test
## Repeatedly Shuffle polarities of data observations
## Take means
## Compare all means with the real-world observed one
null_dist_grade <-
  mosaic::do(4999) *
    mean(
      ~ (course_grade - belief) *
        sample(c(-1, 1), # +/- 1s multiply y
          length(course_grade), # How many +/- 1s?
          replace = T
        ), # select with replacement
      data = exam_grades
    )

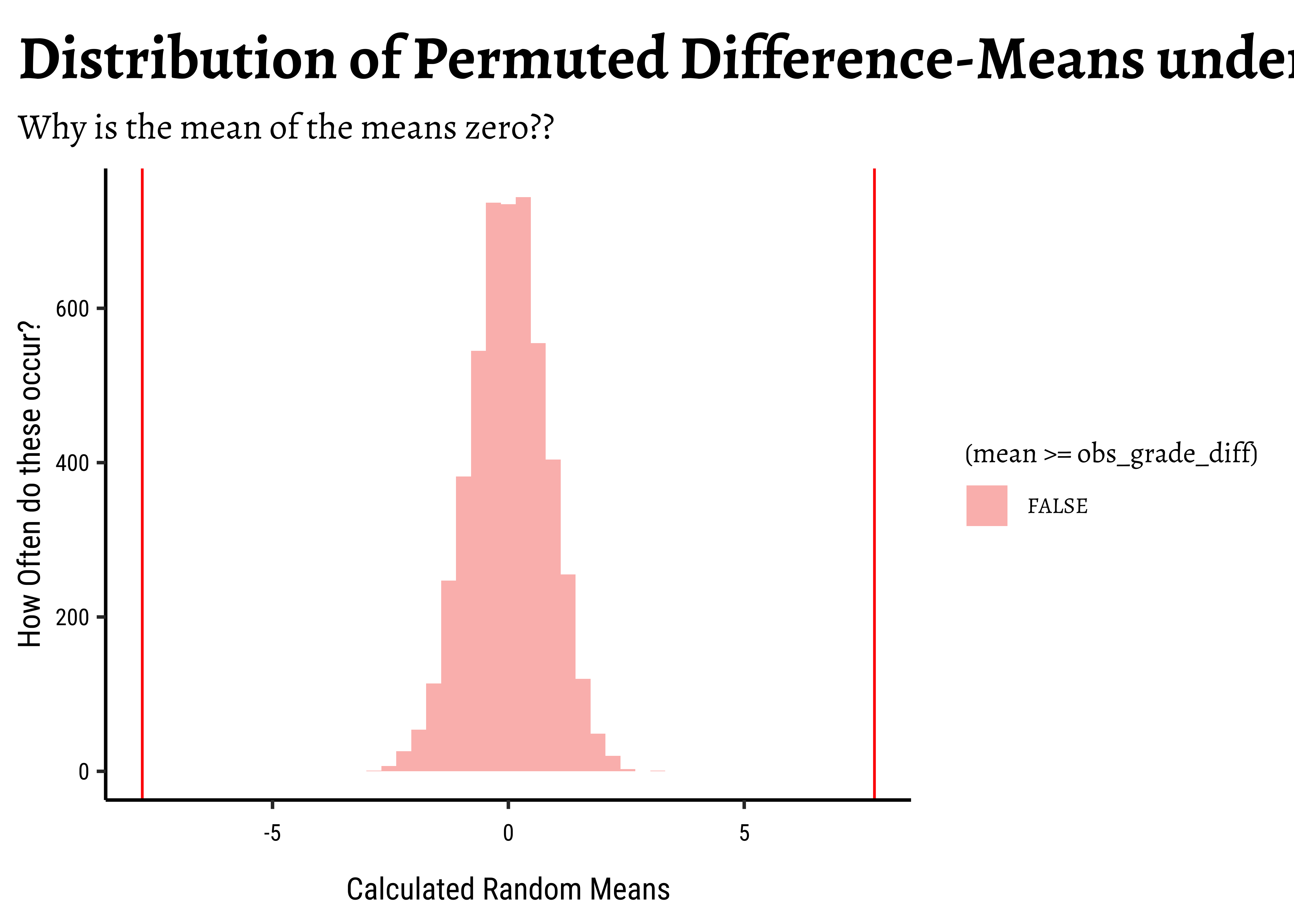
## Plot this NULL distribution
gf_histogram(
  ~mean,
  data = null_dist_grade,
  fill = ~ (mean >= obs_grade_diff),
  bins = 50,
  title = "Distribution of Permuted Difference-Means under Null Hypothesis",
  subtitle = "Why is the mean of the means zero??"
) %>%
  gf_labs(
    x = "Calculated Random Means",
    y = "How Often do these occur?"
  ) %>%
  gf_vline(xintercept = obs_grade_diff, colour = "red") %>%
  gf_vline(xintercept = -obs_grade_diff, colour = "red")

# p-value
# Permutation distributions are always centered around zero. Why?
prop(~ mean >= obs_grade_diff,
  data = null_dist_grade
) +
  prop(~ mean <= -obs_grade_diff,
    data = null_dist_grade
  )
prop_TRUE 
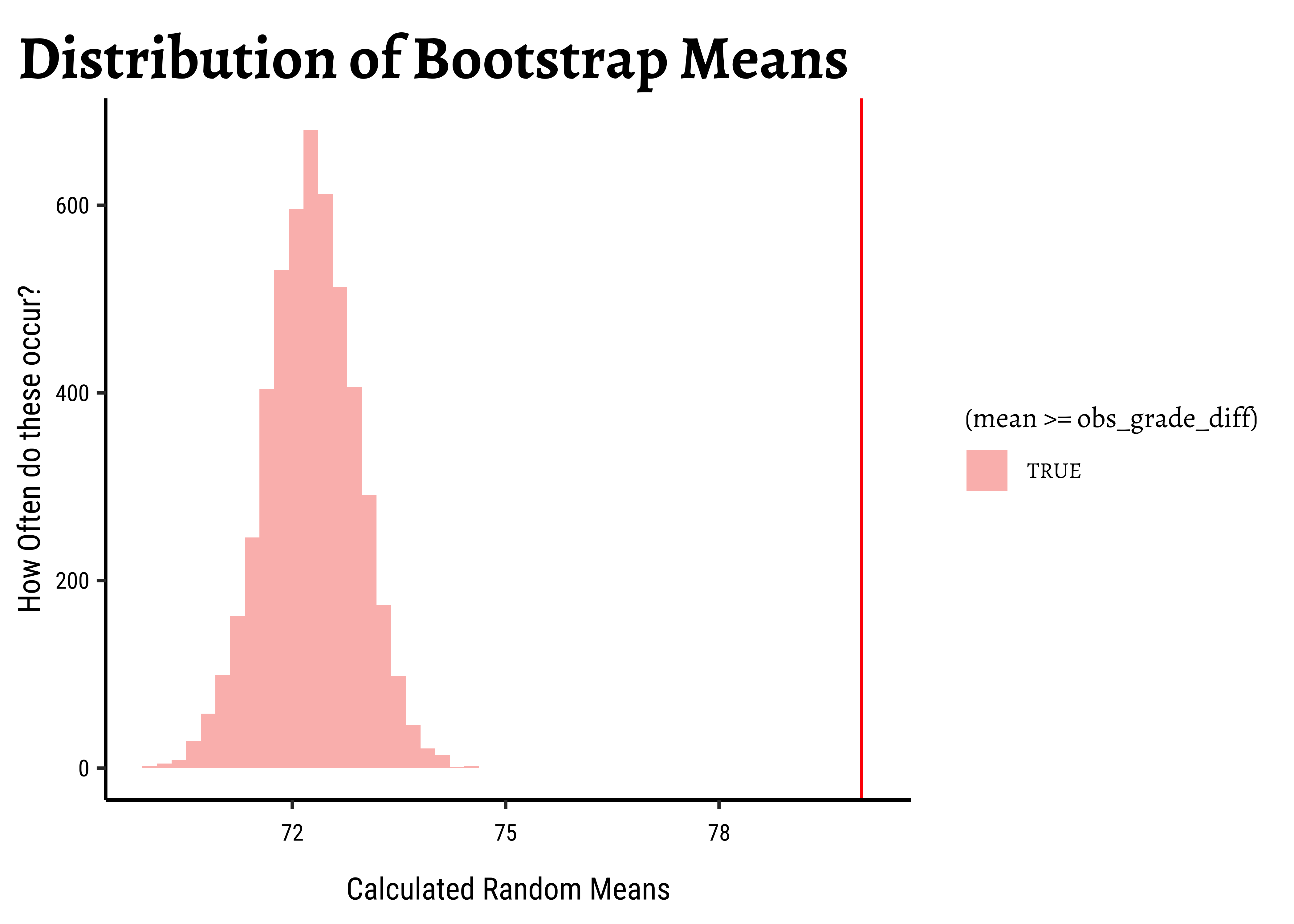
        0

And let us now do the bootstrap test:

null_grade_bs <- mosaic::do(4999) *
  mean(
    ~ sample(course_grade,
      replace = T
    ), # select with replacement
    data = exam_grades
  )

## Plot this NULL distribution
gf_histogram(
  ~mean,
  data = null_grade_bs,
  fill = ~ (mean >= obs_grade_diff),
  bins = 50,
  title = "Distribution of Bootstrap Means"
) %>%
  gf_labs(
    x = "Calculated Random Means",
    y = "How Often do these occur?"
  ) %>%
  gf_vline(xintercept = ~belief, colour = "red")

prop(~ mean >= belief,
  data = null_grade_bs
) +
  prop(~ mean <= -belief,
    data = null_grade_bs
  )
prop_TRUE 
        0

The permutation test shows that we are not able to “generate” the believed mean-difference with any of the permutations. Likewise with the bootstrap, we are not able to hit the believed mean with any of the bootstrap samples.

Hence there is no reason to believe that the belief (80) might be a reasonable one and we reject our NULL Hypothesis that the mean is equal to 80.

Workflow for Inference for a Single Mean

A series of tests deal with one mean value of a sample. The idea is to evaluate whether that mean is representative of the mean of the underlying population. Depending upon the nature of the (single) variable, the test that can be used are as follows:

flowchart TD
    A[Inference for Single Mean] -->|Check Assumptions| B[Normality: Shapiro-Wilk Test shapiro.test\n or\n Anderson-Darling Test]
    B --> C{OK?}
    C -->|Yes\n Parametric| D[t.test]
    C -->|No\n Non-Parametric| E[wilcox.test]
    E <--> G[t.test\n with\n Signed-Ranks of Data]
    C -->|No\n Non-Parametric| P[Bootstrap]
    C -->|No\n Non-Parametric| Q[Permutation]

Wait, But Why?

  • We can only sample from a population, and calculate sample statistics
  • But we still want to know about population parameters
  • All our tests and measures of uncertainty with samples are aimed at obtaining a confident measure of a population parameter.
  • Means are the first on the list!

Conclusion

  • If samples are normally distributed, we use a t.test.
  • Else we try non-parametric tests such as the Wilcoxon test.
  • Since we now have compute power at our fingertips, we can leave off considerations of normality and simply proceed with either a permutation or a boostrap test.

References

  1. OpenIntro Modern Statistics, Chapter #17

  2. Bootstrap based Inference using the infer package: https://infer.netlify.app/articles/t_test

  3. Michael Clark & Seth Berry. Models Demystified: A Practical Guide from t-tests to Deep Learning. https://m-clark.github.io/book-of-models/

  4. University of Warwickshire. SAMPLING: Searching for the Approximation Method use to Perform rational inference by Individuals and Groups. https://sampling.warwick.ac.uk/#Overview

Additional Readings

  1. https://mine-cetinkaya-rundel.github.io/quarto-tip-a-day/posts/21-diagrams/
R Package Citations
Package Version Citation
explore 1.3.2 Krasser (2024)
infer 1.0.7 Couch et al. (2021)
openintro 2.5.0 Çetinkaya-Rundel et al. (2024)
resampledata 0.3.1 Chihara and Hesterberg (2018)
TeachHist 0.2.1 Lange (2023)
TeachingDemos 2.13 Snow (2024)
Çetinkaya-Rundel, Mine, David Diez, Andrew Bray, Albert Y. Kim, Ben Baumer, Chester Ismay, Nick Paterno, and Christopher Barr. 2024. openintro: Datasets and Supplemental Functions from “OpenIntro” Textbooks and Labs. https://CRAN.R-project.org/package=openintro.
Chihara, Laura M., and Tim C. Hesterberg. 2018. Mathematical Statistics with Resampling and r. 2nd ed. Hoboken, NJ: John Wiley & Sons. https://sites.google.com/site/chiharahesterberg/home.
Couch, Simon P., Andrew P. Bray, Chester Ismay, Evgeni Chasnovski, Benjamin S. Baumer, and Mine Çetinkaya-Rundel. 2021. “infer: An R Package for Tidyverse-Friendly Statistical Inference.” Journal of Open Source Software 6 (65): 3661. https://doi.org/10.21105/joss.03661.
Krasser, Roland. 2024. explore: Simplifies Exploratory Data Analysis. https://CRAN.R-project.org/package=explore.
Lange, Carsten. 2023. TeachHist: A Collection of Amended Histograms Designed for Teaching Statistics. https://CRAN.R-project.org/package=TeachHist.
Snow, Greg. 2024. TeachingDemos: Demonstrations for Teaching and Learning. https://CRAN.R-project.org/package=TeachingDemos.
Back to top

Footnotes

  1. https://allendowney.blogspot.com/2016/06/there-is-still-only-one-test.html↩︎

  2. https://stats.stackexchange.com/q/171748↩︎

  3. https://www.r-bloggers.com/2021/11/anderson-darling-test-in-r-quick-normality-check/↩︎

Citation

BibTeX citation:
@online{v.2022,
  author = {V., Arvind},
  title = {🃏 {Inference} for a {Single} {Mean}},
  date = {2022-11-10},
  url = {https://av-quarto.netlify.app/content/courses/Analytics/Inference/Modules/100-OneMean/},
  langid = {en},
  abstract = {Inference Tests for a Single population Mean}
}
For attribution, please cite this work as:
V., Arvind. 2022. “🃏 Inference for a Single Mean.” November 10, 2022. https://av-quarto.netlify.app/content/courses/Analytics/Inference/Modules/100-OneMean/.