EDA: Interactive Correlation Graphs in R

Author

Arvind Venkatadri

Published

July 29, 2025

Abstract

Tests, Tables, and Graphs for Correlations in R

Introduction

We will create Tables for Correlations, and graphs for Correlations in R. As always, we will consistently use the Project Mosaic ecosystem of packages in R (mosaic, mosaicData and ggformula).

Setting up R Packages

library(tidyverse)
library(mosaic) # package for stats, simulations, and basic plots
library(mosaicData) # package containing datasets
library(ggformula) # package for professional looking plots, that use the formula interface from mosaic
library(NHANES) # survey data collected by the US National Center for Health Statistics (NCHS)
library(corrplot) # For Correlogram plots
library(plotly)
library(echarts4r)

Interactive Graphs with echarts4r

We will also start using echarts4r side by side for interactive graphs.

Every function in the package starts with e_.
You start coding a visualization by creating an echarts object with the e_charts() function. That takes your data frame and x-axis column as arguments.
Next, you add a function for the type of chart (e_line(), e_bar(), etc.) with the y-axis series column name as an argument.
The rest is mostly customization! echarts4r takes some effort in getting used to, but it totally worth it!

Case Study #1: Dataset from `mosaicData`

Let us inspect what datasets are available in the package mosaicData.

Run this command in your Console: data(package = “mosaicData”)

The popup tab shows a lot of datasets we could use. Let us continue to use the famous Galton dataset and inspect it: (We will save the inspect output as an R object for use later)

data("Galton")
galton_describe <- inspect(Galton)
galton_describe$categorical

ABCDEFGHIJ0123456789

name <chr>	class <chr>	levels <int>	n <int>	missing <int>	distribution <chr>
family	factor	197	898	0	185 (1.7%), 166 (1.2%), 66 (1.2%) ...
sex	factor	2	898	0	M (51.8%), F (48.2%)

galton_describe$quantitative

ABCDEFGHIJ0123456789

	name <chr>	class <chr>	min <dbl>	Q1 <dbl>	median <dbl>	Q3 <dbl>	max <dbl>	mean <dbl>	sd <dbl>
1	father	numeric	62	68	69.0	71.0	78.5	69.232851	2.470256
2	mother	numeric	58	63	64.0	65.5	70.5	64.084410	2.307025
3	height	numeric	56	64	66.5	69.7	79.0	66.760690	3.582918
4	nkids	integer	1	4	6.0	8.0	15.0	6.135857	2.685156

The inspect command already gives us a series of statistical measures of different variables of interest. As discussed previously, we can retain the output of inspect and use it in our reports: (there are ways of dressing up these tables too)

The dataset is described as:

Try help("Galton") in your Console.

A data frame with 898 observations on the following variables.
- family a factor with levels for each family
- father the father’s height (in inches)
- mother the mother’s height (in inches)
- sex the child’s sex: F or M
- height the child’s height as an adult (in inches)
- nkids the number of adult children in the family, or, at least, the number whose heights Galton recorded.

There is a lot of Description generated by the mosaic::inspect() command ! What can we say about the dataset and its variables? How big is the dataset? How many variables? What types are they, Quant or Qual? If they are Qual, what are the levels? Are they ordered levels? Discuss!

Correlations and Plots

What Questions might we have, that we could answer with a Statistical Measure, or Correlation chart?

Pair-wise Correlation Plot

Q.1 Which are the variables that have significant pair-wise correlations? What polarity are these correlations?

# Pulling out the list of Quant variables from NHANES
galton_quant <- galton_describe$quantitative
galton_quant$name

[1] "father" "mother" "height" "nkids"

GGally::ggpairs(
  Galton,
  columns = c("father", "mother", "height", "nkids"),
  diag = list("densityDiag"),
  title = "Galton Data Correlations Plot"
) %>%
  plotly::ggplotly()

Insight: There are significant, but low value correlations in the Galton dataset. height is best correlated with father ( $0.275$ ). The Scatter Plots shown in the plot also visually demonstrate the (lack of) large value correlations.

We cannot have too many variables in this kind of plot. We will shortly see how to plot correlations when there are a large number of variables.

Heatmap

echarts4r does not have a comprehensive combination plot like what GGally offers. However, we can plot a Correlation Heatmap using echarts4r:

Galton %>%
  select(where(is.numeric)) %>%
  mosaic::cor() %>%
  e_charts(height = 300) %>%
  e_correlations(order = "hclust", visual_map = TRUE) %>%
  e_title("Galton Correlations Heatmap")

Insight: Moving the cursor over the heatmap gives us the an indication of the correlation scores between variables. The visual map slider moves automatically to indicate the scores. We can also move the slider ourselves to “filter” the heatmap!

Question

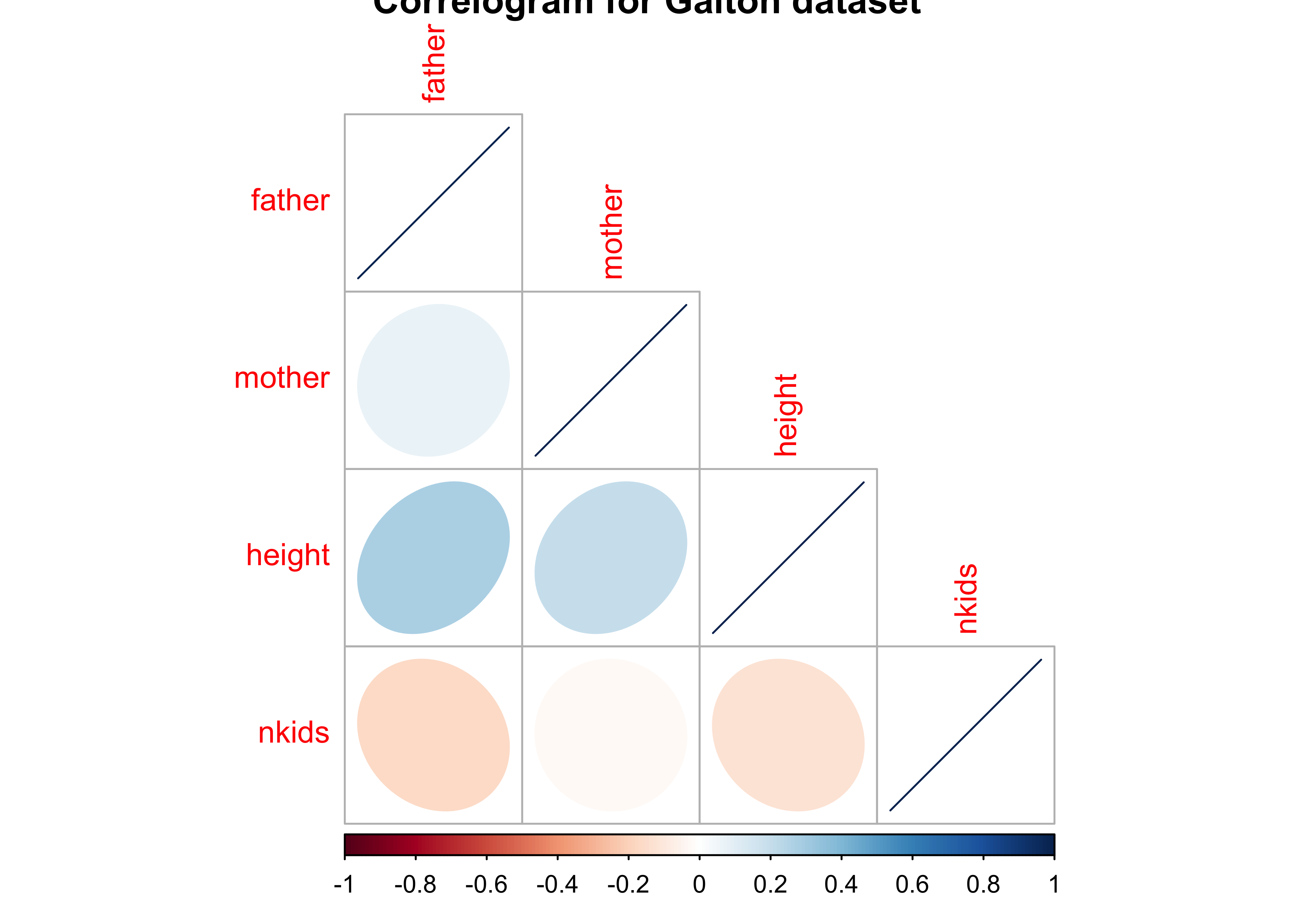
Q.2: Can we plot a Correlogram for this dataset?

# library(corrplot)

galton_num_var <- Galton %>% select(father, mother, height, nkids)
galton_cor <- cor(galton_num_var)
galton_cor %>%
  corrplot(
    method = "ellipse",
    type = "lower",
    main = "Correlogram for Galton dataset"
  )

Insight: Again, height is positively correlated to father and mother as depicted by the rightward-sloping blue ellipses. And height is negatively correlated (very slightly) with nkids, with leftward-sloping reddish ellipses. (See the color palette + legend below the figure).

Question

Q.3: What do the correlation tests tell us?

mosaic::cor_test(height ~ father, data = Galton)
mosaic::cor_test(height ~ mother, data = Galton)


    Pearson's product-moment correlation

data:  height and father
t = 8.5737, df = 896, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.2137851 0.3347455
sample estimates:
      cor 
0.2753548


    Pearson's product-moment correlation

data:  height and mother
t = 6.1628, df = 896, p-value = 1.079e-09
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.1380554 0.2635982
sample estimates:
      cor 
0.2016549

Insight: The tests give us the same values seen before, along with the confidence intervals for the correlation estimate. These represent the uncertainty that exists in our estimates.

Question

Q.4: What does this correlation look when split by sex of Child?

We will use the mosaic function cor_test to get these results:

# For the sons
mosaic::cor_test(height ~ father,
  data = Galton %>% filter(sex == "M")
)
cor_test(height ~ mother, data = Galton %>%
  filter(sex == "M"))


    Pearson's product-moment correlation

data:  height and father
t = 9.1498, df = 463, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.3114667 0.4656805
sample estimates:
      cor 
0.3913174


    Pearson's product-moment correlation

data:  height and mother
t = 7.628, df = 463, p-value = 1.367e-13
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.2508178 0.4125305
sample estimates:
      cor 
0.3341309

# For the daughters
cor_test(height ~ father,
  data = Galton %>% filter(sex == "F")
)
cor_test(height ~ mother,
  data = Galton %>% filter(sex == "F")
)


    Pearson's product-moment correlation

data:  height and father
t = 10.719, df = 431, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.3809944 0.5300812
sample estimates:
      cor 
0.4587605


    Pearson's product-moment correlation

data:  height and mother
t = 6.8588, df = 431, p-value = 2.421e-11
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.2261463 0.3962226
sample estimates:
      cor 
0.3136984

Insight: Son’s heights are correlated more with father than with mother. This trend is even more so for daughters! Hmmm…mother’s influence on children is clearly not with height.

Correlation Tests and Uncertainty

Note how the cor.test reports a correlation score and the p-value for the same. There is also a confidence interval reported for the correlation score, an interval within which we are 95% sure that the true correlation value is to be found. Note that GGally too reports the significance of the correlation scores using *** or **. This indicates the p-value in the scores obtained by GGally; Presumably, there is an internal cor.test that is run for each pair of variables and the p-value and confidence levels are also computed internally.

We can also visualise this uncertainty and the confidence levels in a plot too, using gf_errorbar and a handy set of functions within purrr which is part of the tidyverse: Assuming heights is the target variable we want to correlate every other (quantitative) variable against, we can proceed very quickly as follows:

all_corrs <- Galton %>%
  select(where(is.numeric)) %>%
  # leave off height to get all the remaining ones
  select(-height) %>%
  # perform a cor.test for all variables against height
  purrr::map(
    .x = .,
    .f = \(x) cor.test(x, Galton$height)
  ) %>%
  # tidy up the cor.test outputs into a tidy data frame
  map_dfr(broom::tidy, .id = "predictor")

all_corrs

ABCDEFGHIJ0123456789

predictor <chr>	estimate <dbl>	statistic <dbl>	p.value <dbl>	parameter <int>	conf.low <dbl>	conf.high <dbl>	method <chr>	alternative <chr>
father	0.2753548	8.573704	4.354588e-17	896	0.2137851	0.33474554	Pearson's product-moment correlation	two.sided
mother	0.2016549	6.162793	1.079105e-09	896	0.1380554	0.26359819	Pearson's product-moment correlation	two.sided
nkids	-0.1269101	-3.829800	1.371780e-04	896	-0.1907472	-0.06200411	Pearson's product-moment correlation	two.sided

all_corrs %>%
  e_charts(predictor) %>%
  e_bar(estimate, colorBy = "data", legend = FALSE) %>%
  e_error_bar(lower = conf.low, upper = conf.high) %>%
  e_y_axis(
    name = "Correlation with `height`",
    nameLocation = "middle", nameGap = 35
  ) %>%
  e_x_axis(
    name = "Parameter", nameLocation = "center",
    nameGap = 35, type = "category"
  ) %>%
  e_tooltip()

all_corrs %>%
  mutate(sd = (conf.high - conf.low) / 2) %>%
  plot_ly() %>%
  add_bars(
    y = ~estimate, x = ~predictor,
    error_y = ~ list(array = sd, color = "black")
  )

Insight: We can clearly see the size of the correlations and the confidence intervals marked in this plot. father has somewhat greater correlation with children’s height, as compared to mother. nkids seems to matter very slightly, in a negative way.

This kind of plot will be very useful when we pursue linear regression models.

Question

Q.5. How can we show this correlation in a set of Scatter Plots + Regression Lines? Can we recreate Galton’s famous diagram?

# For the father
Galton %>%
  group_by(sex) %>%
  e_charts(father, height = 300) %>%
  e_scatter(height, symbol_size = 8) %>%
  e_lm(height ~ father, legend = FALSE) %>%
  e_x_axis(
    name = "father", nameLocation = "middle", nameGap = 35,
    min = 60, max = 80
  ) %>%
  e_y_axis(
    name = "height", nameLocation = "middle", nameGap = 35,
    min = 50, max = 80
  ) %>%
  e_tooltip()
# for the mother
Galton %>%
  group_by(sex) %>%
  e_charts(mother, height = 300) %>%
  e_scatter(height, symbol_size = 8) %>%
  e_lm(height ~ mother, legend = FALSE) %>%
  e_x_axis(
    name = "mother", nameLocation = "middle", nameGap = 35,
    min = 55, max = 75
  ) %>%
  e_y_axis(
    name = "height", nameLocation = "middle", nameGap = 35,
    min = 50, max = 80
  ) %>%
  e_tooltip()

Insight: Visibly the scatter plots are slightly tilted upward to the right, showing a positive correlation for both sons’ and daughters’ heights with that of the father and mother.

Galton’s Plot

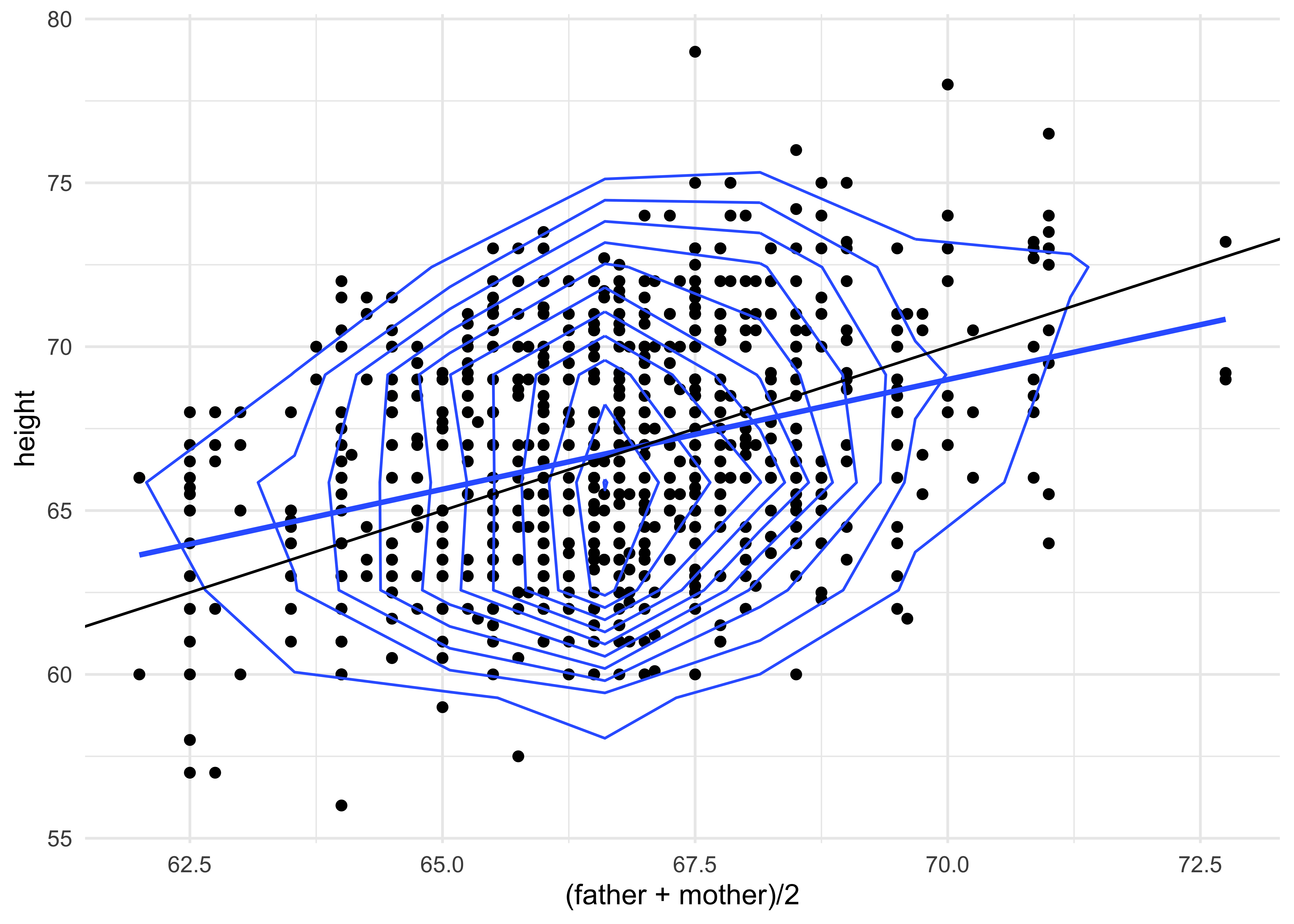
An approximation to Galton’s famous plot (see Wikipedia):

gf_point(height ~ (father + mother) / 2, data = Galton) %>%
  gf_smooth(method = "lm") %>%
  gf_density_2d(n = 8) %>%
  gf_abline(slope = 1) %>%
  gf_theme(theme_minimal())

Insight: How would you interpret this plot¹? As yet we are not able to reproduce this with charts4r.

Case Study #2: Dataset from `NHANES`

We will “live code” this in class!

Conclusion

We have a decent Correlations related workflow in R:
- load the dataset
- inspect the dataset, identify Quant and Qual variables
- Develop Pair-Wise plots + Correlations using GGally::ggpairs()
- Develop Correlogram corrplot::corrplot
- Check everything with a cor_test
- Use purrr + cor.test to plot correlations and confidence intervals for multiple Quant variables
- Plot scatter plots using gf_point.
- Add extra lines using gf_abline() to compare hypotheses that you may have.

Footnotes

https://www.researchgate.net/figure/Galtons-smoothed-correlation-diagram-for-the-data-on-heights-of-parents-and-children_fig15_226400313↩︎

Introduction

Setting up R Packages

Case Study #1: Dataset from mosaicData

Correlations and Plots

Correlation Tests and Uncertainty

Case Study #2: Dataset from NHANES

Conclusion

Footnotes

Case Study #1: Dataset from `mosaicData`

Case Study #2: Dataset from `NHANES`