🏃 Change

If you wish to go anywhere, you must run twice as fast as that.

Abstract

How one variable changes with another

What graphs will we see today?

Variable #1	Variable #2	Chart Names	Chart Shape
Quant	Quant	Scatter Plot

What kind of Data Variables will we choose?

No	Pronoun	Answer	Variable/Scale	Example	What Operations?
1	How Many / Much / Heavy? Few? Seldom? Often? When?	Quantities, with Scale and a Zero Value.Differences and Ratios /Products are meaningful.	Quantitative/Ratio	Length,Height,Temperature in Kelvin,Activity,Dose Amount,Reaction Rate,Flow Rate,Concentration,Pulse,Survival Rate	Correlation

Inspiration

Figure 1: ScatterPlot Inspiration http://www.calamitiesofnature.com/archive/?c=559

Does belief in Evolution depend upon the GSP of of the country? Where is the US in all of this? Does the Bible Belt tip the scales here?

And India?

How do these Chart(s) Work?

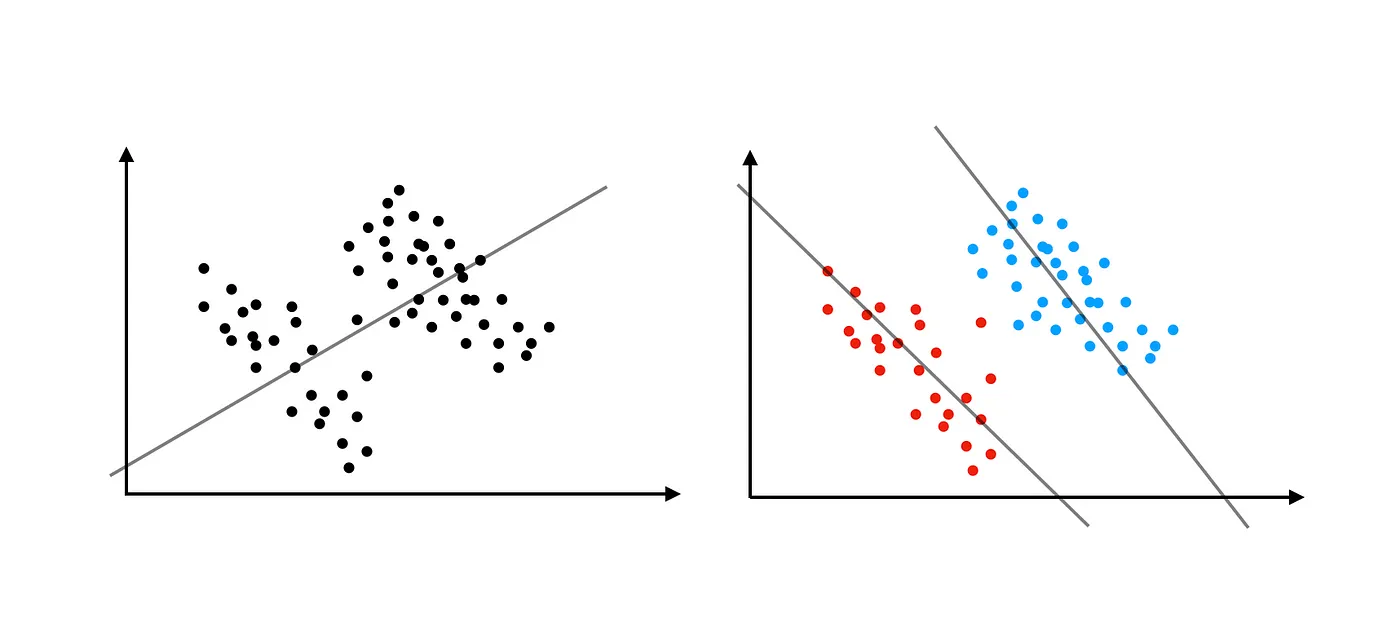
Scatter Plots take two separate Quant variables as inputs. Each of the variables is mapped to a position, or coordinate: one for the X-axis, and the other for the Y-axis. Each pair of observations from the two Quant variables ( which would be in one row!) give us a point in the Scatter Plot.

Looking at these clouds of points gives us an intuitive sense of the relationship between the two Quant variables, how one varies with the other. A cloud that slopes upward to the right indicates a positive relationship between the two; a cloud that slopes down to the right indicates a negative one. An amorphous cloud that does not discernibly slope in either way would lead us to infer that there is little or no relationship between the variables.

Slope and the Correlation Coefficient are Related

Under the assumption of a linear relationship between the two Quant variables, we plot a straight trend line, or regression line through the cloud of points, as a line that best represents that linear relationship. The slope of the regression line is directly linked to the Pearson Correlation Coefficient between the two variables.

Plotting a Scatter Plot

Using Orange

We can use the now (overly) familiar iris dataset to plot our first scatter plot. Download the workflow file below:

Figure 2: Iris Scatter Plot

• Try setting shapes and colours, and try plotting a “regression line”. Do you get one line, or several? Why, or why not? How can you switch between the two “methods”?
• Try other pairs of Quant variables in the dataset.
• Which plot is the most informative? Why?

Using RAWgraphs

https://youtu.be/FafXHMmau1M

Using DataWrapper

https://academy.datawrapper.de/article/65-how-to-create-a-scatter-plot

What is the Story here?

• There are three species of iris flowers and they are “separable” based on combinations of their quantitative measurements.
• Some pairs of Quant variables create Scatter Plots that are quite disjoint and allow easy identification of the species variable.
• In a ML model for this dataset, the species variable is most likely to be the target variable while the rest are predictors.

Dataset: Cancer

Let us examine a fairly complex dataset pertaining to cancer, and analyze that with scatter plots.

We can use the same Workflow as before.

Examine the Data

Figure 3: Cancer Data Table

From Figure 3, we see that there is one Qual column Diagnosis, and all the remaining 31 columns seem to be some Quant measurements of a total of 569 tumours. (Not all columns are visible)

Figure 4: Cancer Data Summary Table #1

Figure 4 gives is histograms and statistics of all the 32 columns. Most histograms seem roughly symmetric, but a detailed look must be taken.

Figure 5: Cancer Data Summary Table #2

In Figure 5, we see that there is some imbalance between the counts for the one Qual variable, Diagnosis.

Data Dictionary

Quantitative Data

“Id”
“Radius (mean)”	“Texture (mean)”
“Perimeter (mean)”	“Area (mean)”
“Smoothness (mean)”	“Compactness (mean)”
“Concavity (mean)”	“Concave points (mean)”
“Symmetry (mean)”	“Fractal dimension (mean)”
“Radius (se)”	“Texture (se)”
“Perimeter (se)”	“Area (se)”
“Smoothness (se)”	“Compactness (se)”
“Concavity (se)”	“Concave points (se)”
“Symmetry (se)”	“Fractal dimension (se)”
“Radius (worst)”	“Texture (worst)”
“Perimeter (worst)”	“Area (worst)”
“Smoothness (worst)”	“Compactness (worst)”
“Concavity (worst)”	“Concave points (worst)”
“Symmetry (worst)”	“Fractal dimension (worst)”

• Many of the Quant variables seem to be mean measurements, with the mean presumably taken over several “sites” within the same tumour.
• Along with the mean, there are also measurements of se or standard error which is, roughly speaking, a measure of the standard deviation of the multiple measurements made. So for instance, Area(mean) and Area(se) are pairs of measurements created using multiple “sites” or “cross-sections” on one tumour.
• Some other variables are labelled as worst, which may be either the max or min of such a set of “multi-site” tumour measurements.

May the (data) Source be with you

It is important to note that these are (educated?) guesses; one is best off connecting with the person/agency that provided the data for a precise understanding of variables. This will prevent nonsensical plots/models and inferences from showing up in your work.

Qualitative Data

• Diagnosis: (text) (B)enign, or (M)alignant

Research Questions

Question

Q1. Are the mean and se observations correlated, for a particular variable?

(a) Cancer Scatter Plot #1

(b) Cancer Scatter Plot #2

(c) Cancer Scatter Plot #3

(d) Cancer Scatter Plot #4

Figure 6

Question

Q2. Are the mean and worst observations correlated, for a particular variable?

(a) Cancer Scatter Plot #5

(b) Cancer Scatter Plot #6

(c) Cancer Scatter Plot #7

(d) Cancer Scatter Plot #8

Figure 7

What is the Story Here?

From Figure 7 (a), we see that the area(mean) and area(se) are somewhat correlated; moreover the correlation is slightly higher for the malignant tumours ( red dots, appropriately…). This trend shows up also for radius in Figure 7 (b), and for fractaldimension in Figure 7 (d). However, for smoothness, we see much lower correlation {#fig-cancer-smoothness-mean-se}.

For the mean vs worst scatter plots, we see decent correlations all around, with each of the graphs showing clouds tilted upward to the right.

Simpson’s Paradox

Try to remove colours and then plot a regression line. This usually gives a more clear idea of the correlation, without running into problems such as the Simpson’s Paradox:

Figure 8: Simpson’s Paradox

And see also this:

A Variant

Your Turn

1. Try to play this online Correlation Game

2. Try this dataset on School Expenditure and Grades.

3. Gas Prices and Consumption, described here. Note the log-transformed Quant data…why do you reckon this was done in the data set itself?

4. Horror Movies (Bah.You awful people..)

5. Food Delivery Times

Wait, But Why?

• Scatter Plots, when they show “linear” clouds, tell us that there is some relationship between two Quant variables we have just plotted
• If so, then if one is the target variable you are trying to design for, then the other independent, or controllable, variable is something you might want to design with.
• Always, always, plot and test your data! Both numerical summaries and graphical summaries are necessary! See below!!

And How about these datasets?

dataset	mean_x	mean_y	std_dev_x	std_dev_y	corr_x_y
away	54.26610	47.83472	16.76983	26.93974	-0.0641284
bullseye	54.26873	47.83082	16.76924	26.93573	-0.0685864
circle	54.26732	47.83772	16.76001	26.93004	-0.0683434
dino	54.26327	47.83225	16.76514	26.93540	-0.0644719
dots	54.26030	47.83983	16.76774	26.93019	-0.0603414
h_lines	54.26144	47.83025	16.76590	26.93988	-0.0617148
high_lines	54.26881	47.83545	16.76670	26.94000	-0.0685042
slant_down	54.26785	47.83590	16.76676	26.93610	-0.0689797
slant_up	54.26588	47.83150	16.76885	26.93861	-0.0686092
star	54.26734	47.83955	16.76896	26.93027	-0.0629611
v_lines	54.26993	47.83699	16.76996	26.93768	-0.0694456
wide_lines	54.26692	47.83160	16.77000	26.93790	-0.0665752
x_shape	54.26015	47.83972	16.76996	26.93000	-0.0655833

Yes, you did want to plot these in Orange, didn’t you? Here is the data then!!

Warning

• Can selling more ice-cream make people drown?
• Use your head about pairs of variables. Do not fall into this trap)

References

1. Rohrer JM. Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data. Advances in Methods and Practices in Psychological Science. 2018;1(1):27-42. https://doi.org/10.1177/2515245917745629 PDF

2. Case Study on Horror Movies. (Arvind: Bah.) https://notawfulandboring.blogspot.com/2024/04/using-pulse-rates-to-determine-scariest.html

3. The Datasaurus Package: https://cran.r-project.org/web/packages/datasauRus/vignettes/Datasaurus.html

4. A superb web-scrolly on Sustainable Development Goals (SDGs)s! Go and see!!https://datatopics.worldbank.org/sdgatlas/goal-1-no-poverty?lang=en

5. Hunter, W. G. (1981). Six Statistical Tales. The Statistician, 30(2), 107. doi:10.2307/2987563. https://sci-hub.ru/10.2307/2987563

6. A cartoon+interactive explanation of Simpson’s Paradox. Real fun! https://pwacker.com/simpson.html

Figure 1: ScatterPlot Inspiration http://www.calamitiesofnature.com/archive/?c=559 Figure 2: Iris Scatter Plot Figure 3: Cancer Data Table Figure 4: Cancer Data Summary Table #1 Figure 5: Cancer Data Summary Table #2 Figure 6 (a): Cancer Scatter Plot #1 Figure 6 (b): Cancer Scatter Plot #2 Figure 6 (c): Cancer Scatter Plot #3 Figure 6 (d): Cancer Scatter Plot #4 Figure 7 (a): Cancer Scatter Plot #5 Figure 7 (b): Cancer Scatter Plot #6 Figure 7 (c): Cancer Scatter Plot #7 Figure 7 (d): Cancer Scatter Plot #8 Figure 8: Simpson’s Paradox