The TRIZ Chronicles: A TRIZ Analysis of a Recent Spotify Ad

Harrdy Sandhu and Getting the Veggies

TRIZ
Author

Arvind Venkatadri

Published

January 9, 2023

Modified

Invalid Date

Abstract
Punjabi Pop and Getting the Veggies

Introduction

Here we go with another of my TRIZ Chronicles. The first edition analysing the famous movie Lawrence of Arabia is here.

The recent series of ads by Spotify have been very well received, by the ad industry as well. There have been several of these ads, each with a solid little story and a great punch line. There is one popular one that I have selected here, featuring a Mother shopping for veggies, while her son watches (and “listens”) to her bargaining with the shopkeeper. Here I take just that highly effective ad and interpret it from a TRIZ viewpoint.

This piece stems from my teaching a course on Creative Thinking and Problem Solving based on TRIZ, titled Play and Invent, over the past 8 years or more at the Srishti Manipal Institute of Art, Design, and Technology, Bangalore, India. (https://srishtimanipalinstitute.in).

The Famous Spotify Ad

Let us watch the Spotify ad first, before analyzing it!

The Young Man’s Problem

In order to make a story out of this, I want make a Protagonist out the young man in the ad. It is he who has the problem and he who is going to apply TRIZ to solve it. I discuss the source of his Problem and give an analysis of the Problem from a (classical) TRIZ perspective, including the formulation of the Contradiction, Identification of Causes, the statement of the Ideal Final Result, and finally using the TRIZ Contradiction Matrix to find Inventive Principles, that lead to the solution, which of course, is meant to unerringly include Spotify !

First a philosophical digression:—

Several authors have taken a Game View of life. James P Carse’s famous book titled Finite and Infinite Games speaks of Play, Types of Games, Rules, Winning and our own aims in the Game itself. A similar articulation is, in my opinion, that of Mihaly Csikszentlmihalyi in his concept of Flow, shown here below:

From Sketchplanations

From Sketchplanations

When the Game presents very little Challenge, we are bored. When the Game demands extreme skills the challenge is too much for us and we experience anxiety. When the Challenge presented is just barely matched by our Skill, we are in the zone of Flow, or what I call Play.

A good metaphoric image for this experience is as follows:— that we live in a space where the Floor of Boredom is always rising and would crush us against our Ceiling of Anxiety. One Way to deal with this is to develop more Skills and push the Ceiling away, effectively moving into the zone of Flow. Another Way of looking at this is what Carse suggests: When Play is no longer possible, change the Game.

So what does all this have to do with getting veggies?

The ad is, in my opinion, all about Boredom, and how to avoid it. And not offend anybody. The Young Man (hereinafter, “YM”) simply has to accompany his Mom, and be there while she gets the veggies. I will exaggerate his irritation and his boredom at the risk of offending young people likely to read this, and say that he would rather not be there but he does not want to hurt Mom.

We are now ready for the TRIZ based Analysis of this Problem!

A TRIZ Analysis of a Visit to the Subzi Mandi

For a TRIZ workflow, we proceed as before:

First, using the method described in Open Source TRIZ, we identify knobs or parameters within the situation and see how turning these could lead to identifying a Cause for a Problem in the form of a Contradiction.

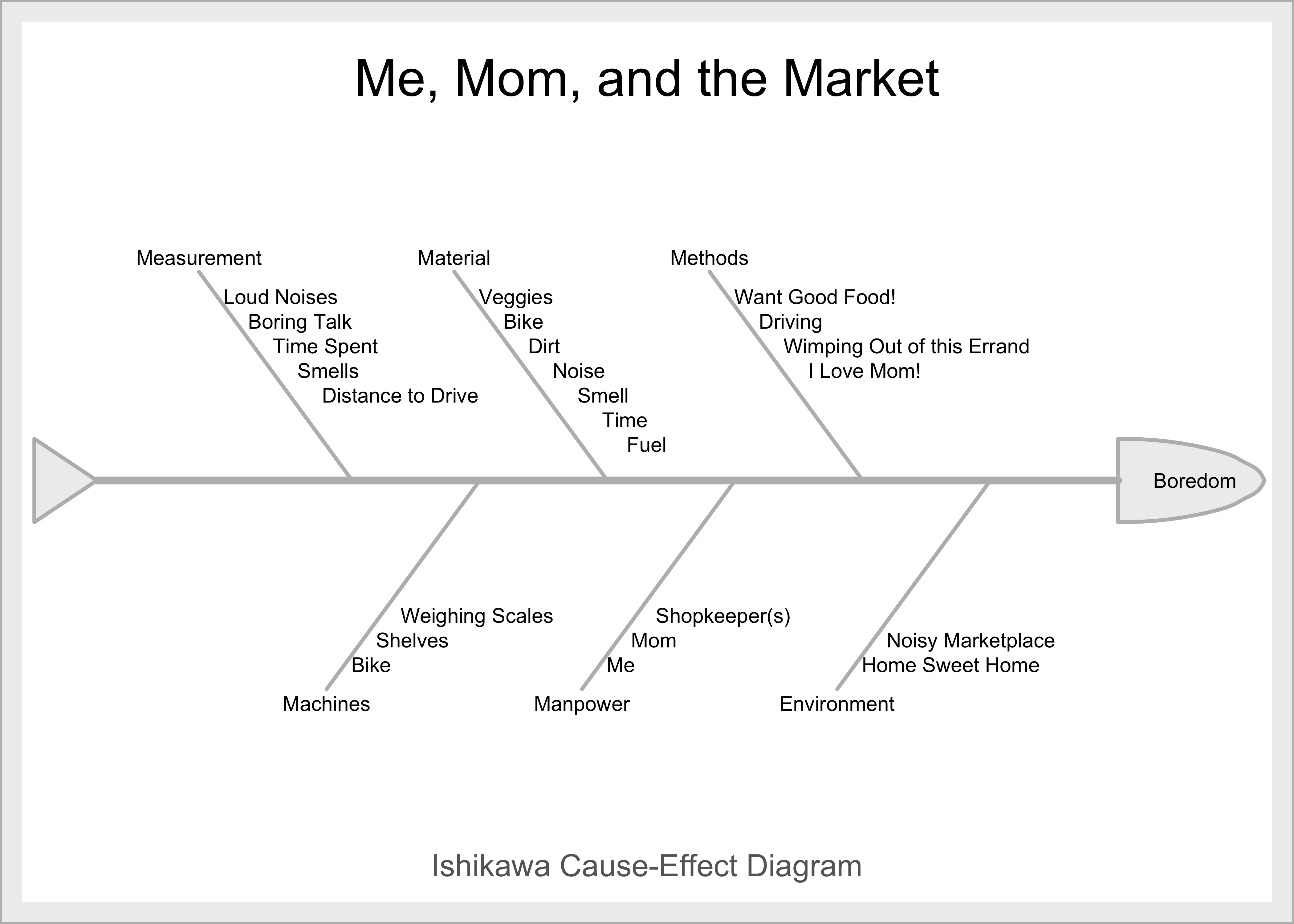
Here below is a quick Ishikawa Diagram to help us identify the Parameters of this Problem:

Turning the knobs/parameters in the Ishikawa Diagram, it seems that if the YM goes to the market with Mom, he would most likely get bored, but would please Mom. If he doesn’t go, then he chills at home, but Mom is going to justifiably furious. Herein lies the Contradiction, which we can now specify as an Administrative Contradiction(AC) in plain English:

AC: The YM wants to chill at home but Mom wants him to take her veggie shopping. He has to put up with the Waste of Time, and being bored, and Stress at being away from friends.

Next, based on this Contradiction and the inspection of the Ishikawa Diagram above, we are now ready to define a TRIZ Ideal Final Result:

IFR: The YM must go to the Market and not be bored.

Note again the impossible sounding way of expressing the IFR! One needs practice, like the Queen in Alice in Wonderland, who could think of Six Impossible Things before Breakfast ! Also note there could be other ways of specifying the IFR. See below, section Alternative Ideas for IFR.

Let us take the AC and convert it into a Technical Contradiction(TC), keeping this IFR in mind. We will look at the 48 TRIZ Parameters in the TRIZ Contradiction Matrix (PDF) and see which Parameter we want to improve, while not worsening another. Here is what we can obtain. We will analyze each Contradiction both ways1:

- TC 1: Improve Loss of Time (26) and not worsen Effect of External Harmful Factors (30)

- TC 2: Improve Increase Productivity (44) and not worsen Stress (19)

Here we choose these Parameters based on our IFR that while going to the Market may be unavoidable, Boredom need not ensue. Parameters chosen from the TRIZ Matrix can be thought of as metaphors for the knobs that lie within our AC. Going from the AC to the TC is an act of making metaphors. We could easily have chosen the Parameter Noise(29) as the “metaphoric thing” to avoid, but the current IFR doesn’t quite support that. There is here a considerable flexibility and possibility for imaginative interpretations of the AC, but using the language of TRIZ.

We could also formulate a Physical Contradiction(PC)2:

PC: The YM must be in the market and not be in the market at the same time.

which is aimed squarely at one of the Assumptions in the Problem, that the YM simply has to go. Again, if the IFR is formulated differently we could obtain a very different set of AC and PC. See below, section Alternative Ideas for IFR.

In a future post, we will deal with using the PC and the TRIZ Separation Principles to solve Problems.

Solving the Technical Contradiction

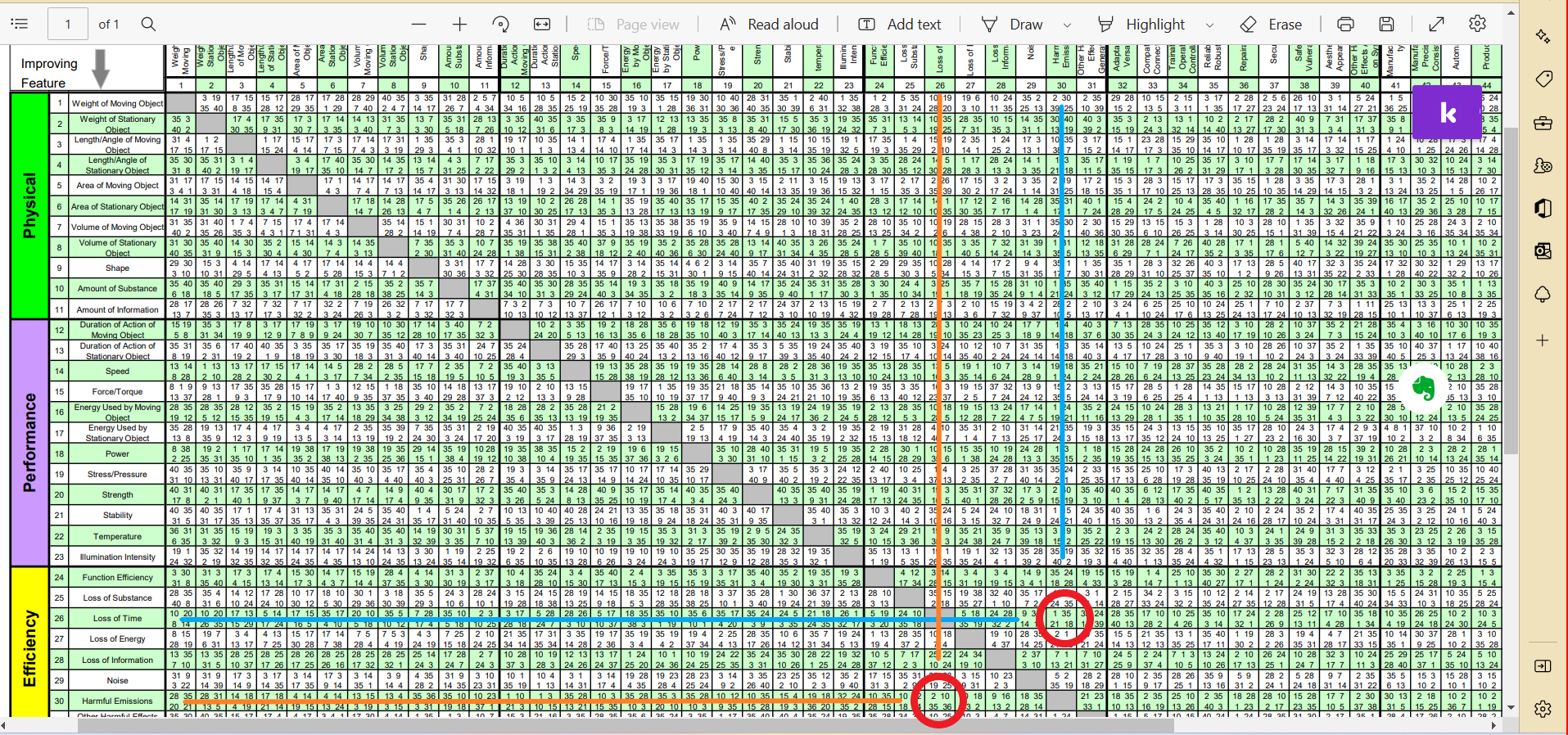
Let us take the both the TC-s into the Contradiction Matrix and arrive at the list of TRIZ Inventive Principles. Here is the Matrix solution for TC-1 in the figure below:


The two squares for the TC1 have been circled in red, solving TC-1.

The Inventive Principles are:(TC1, TC2, both ways)

  1. 1(Segmentation)

  2. 35(Parameter Change)

  3. 21(Skipping)

  4. 18(Mechanical Vibration) (!!)

  5. 2(Taking Out/Separation)

  6. 10(Prior Action)

  7. 36(Phase Transitions)

    and with TC2:

  8. 3(Local Quality)

  9. 14(Spheroidality/Curvature)

  10. 9(Preliminary Anti-Action)

  11. 37(Thermal Expansion)

  12. 40(Composite Materials)

  13. 25(Self Service)

  14. 24(Intermediary)

That is a considerable list for us to try to use!! Let us apply some these Inventive Principles! Viewing these Inventive Principles as we Generalized Solutions we try to map these back into the Problem at hand:

  • 35(Parameter Change): Which Parameter to change? Location? No. Sound? Change the “Bargaining Talk” into what? Sweet Musical Lyrics!!🎵🤣
  • 18(Mechanical Vibration) : What, make noise of your own? Yes! Play Music !!🔉 🤣
  • 14(Spheroidality): Wear “spherical” headphones!!🎧! Create a “sound sphere”! This is a long shot!!
  • 3(Local Quality): also indicates the creation of a “local” cocoon around the YM, but needs to be combined with 18(Mechanical Vibration) to truly arrive at the musical solution!

One could make decent interpretations of 2(Taking Out/Separation), and 24(Intermediary), but we are already there! The rest are perhaps (at least to me!) not very evocative, unless 37(Thermal Expansion) means “throw a temper tantrum at Mom”? Never! So there you have it! The Cinderella song played on Spotify becomes not just a noise canceller but actually seems to substitute the very conversation between Mom and the vendor. And the YM has successfully attained Flow ! And the IFR too, since with the music in his head, he is effectively “in the marketplace and not in the marketplace at the same time!

And I attained Flow in writing this!!

Alternative Ideas for IFR

We note in passing that there is more than one way of formulating the Ideal Final Result. Here are two more examples:

IFR2: The veggies should arrive without (the YM) going to the Market

IFR3: Food should be prepared without having to go buy veggies.

Clearly these are at least as good as the one we have chosen, sounding nicely “impossible” in their own right! The point is that in the analysis of the Problem, we do need to ask Who has the Problem, as we did, and the IFR needs to stem from there. These alternative IFRs could well be the Voice of (another) Customer.

If there is any interesting situation that could be analyzed with TRIZ, please send me a DM! Thanks !

References

  1. James P Carse, Finite and Infinite Games, Free Press, 1986. ISBN: 0-02-905980-1
  2. Mihaly Csikszentmihalyi, Creativity, Flow, and the Psychology of Discovery and Invention. Harper Perennial; Reprint edition (August 6, 2013)
  3. Jack Hipple, The Ideal Result and How to Achieve It. Springer; 2012th edition (June 26, 2012)
  4. Valery Souchkov, Defining Contradictions. http://www.xtriz.com/Training/TRIZ_DefineContradiction_Tutorial.pdf
Back to top

Footnotes

  1. The Contradiction Matrix is not quite symmetric, so stating the Contradiction both ways allows us to access a slightly larger set of Inventive Principles from two cells of the Matrix.↩︎

  2. Arriving at Physical Contradictions is not always easy! If we can, then there are a very crisp set of TRIZ Separation Principles that we can apply to solve the Problem.↩︎