Tutorial on Correlations in R

Author

Arvind Venkatadri

Published

November 22, 2022

Modified

May 21, 2024

Abstract

Tests, Tables, and Graphs for Correlations in R

Introduction

We will create Tables for Correlations, and graphs for Correlations in R. As always, we will consistently use the Project Mosaic ecosystem of packages in R (mosaic, mosaicData and ggformula).

Setting up R Packages

library(tidyverse)
library(mosaic) # package for stats, simulations, and basic plots
library(ggformula) # package for professional looking plots, that use the formula interface from mosaic
library(skimr)
library(GGally)
library(corrplot) # For Correlogram plots
library(broom) # to properly format stat test results

library(mosaicData) # package containing datasets
library(NHANES) # survey data collected by the US National Center for Health Statistics (NCHS)

All R functions seen in the code are clickable links that take you to online documentation about the function. Try!

The Formula interface

Note the standard method for all commands from the mosaic package:

goal( y ~ x | z, data = mydata, …)

With ggformula, one can create any graph/chart using:

gf_geometry(y ~ x | z, data = mydata)

mydata %>% gf_geometry( y ~ x | z )

The second method may be preferable, especially if you have done some data manipulation first! More about this later!

Case Study 1: Galton Dataset from `mosaicData`

Let us inspect what datasets are available in the package mosaicData. Run this command in your Console:

# Run in Console
data(package = "mosaicData")

The popup tab shows a lot of datasets we could use. Let us continue to use the famous Galton dataset and inspect it:

data("Galton")

Inspecting the Data

The inspect command already gives us a series of statistical measures of different variables of interest. As discussed previously, we can retain the output of inspect and use it in our reports: (there are ways of dressing up these tables too)

galton_describe <- inspect(Galton)

galton_describe$categorical

ABCDEFGHIJ0123456789

name <chr>	class <chr>	levels <int>	n <int>	missing <int>	distribution <chr>
family	factor	197	898	0	185 (1.7%), 166 (1.2%), 66 (1.2%) ...
sex	factor	2	898	0	M (51.8%), F (48.2%)

galton_describe$quantitative

ABCDEFGHIJ0123456789

	name <chr>	class <chr>	min <dbl>	Q1 <dbl>	median <dbl>	Q3 <dbl>	max <dbl>	mean <dbl>	sd <dbl>
1	father	numeric	62	68	69.0	71.0	78.5	69.232851	2.470256
2	mother	numeric	58	63	64.0	65.5	70.5	64.084410	2.307025
3	height	numeric	56	64	66.5	69.7	79.0	66.760690	3.582918
4	nkids	integer	1	4	6.0	8.0	15.0	6.135857	2.685156

Try help("Galton") in your Console. The dataset is described as:

A data frame with 898 observations on the following variables.
- family a factor with levels for each family
- father the father’s height (in inches)
- mother the mother’s height (in inches)
- sex the child’s sex: F or M
- height the child’s height as an adult (in inches)
- nkids the number of adult children in the family, or, at least, the number whose heights Galton recorded.

There is a lot of Description generated by the mosaic::inspect() command ! Let us also look at the output of skim:

skimr::skim(Galton)

Data summary
Name	Galton
Number of rows	898
Number of columns	6
_______________________
Column type frequency:
factor	2
numeric	4
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
family	0	1	FALSE	197	185: 15, 166: 11, 66: 11, 130: 10
sex	0	1	FALSE	2	M: 465, F: 433

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
father	1	69.23	2.47	62	68	69.0	71.0	78.5	▁▅▇▂▁
mother	1	64.08	2.31	58	63	64.0	65.5	70.5	▂▅▇▃▁
height	1	66.76	3.58	56	64	66.5	69.7	79.0	▁▇▇▅▁
nkids	1	6.14	2.69	1	4	6.0	8.0	15.0	▃▇▆▂▁

What can we say about the dataset and its variables? How big is the dataset? How many variables? What types are they, Quant or Qual? If they are Qual, what are the levels? Are they ordered levels? Which variables could have relationships with others? Why? Write down these Questions!

Correlations and Plots

What Questions might we have, that we could answer with a Statistical Measure, or Correlation chart?

Questions

How does children’s height correlate with that of father and mother? Is this relationship also affected by sex of the child?

With this question, height becomes our target variable, which we should always plot on the dependent y-axis.

# Pulling out the list of Quant variables from NHANES
galton_quant <- galton_describe$quantitative
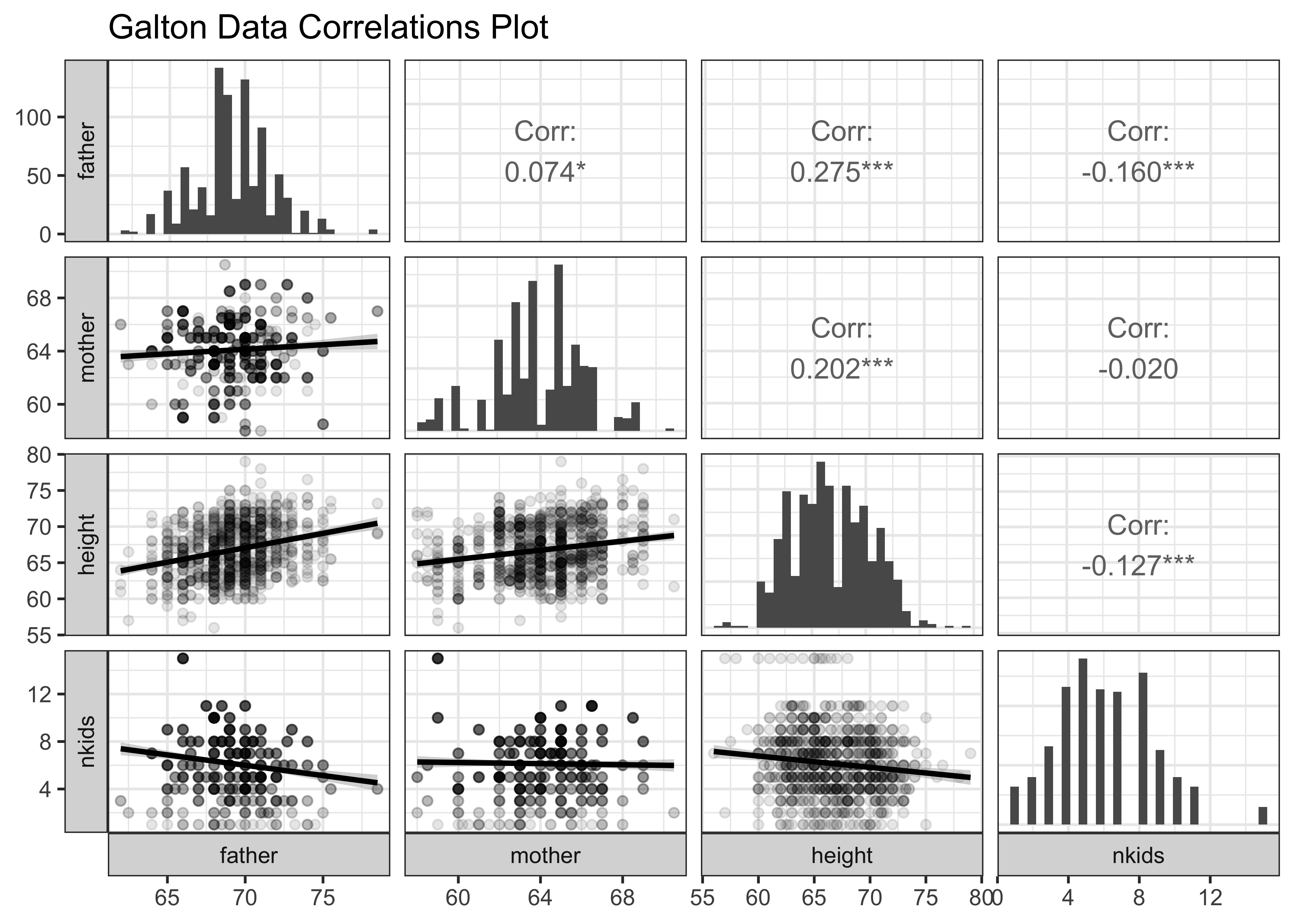
galton_quant$name

[1] "father" "mother" "height" "nkids"

GGally::ggpairs(
  Galton,
  
  # Choose the variables we want to plot for
  columns = c("father", "mother", "height", "nkids"),
  
  switch = "both", # axis labels in more traditional locations
  progress = FALSE, # no compute progress messages needed
  
  # Choose the diagonal graphs (always single variable! Think!)
  diag = list(continuous = "barDiag"), # choosing histogram,not density
  
  # Choose lower triangle graphs, two-variable graphs
  lower = list(continuous = wrap("smooth", alpha = 0.1)),
  
  title = "Galton Data Correlations Plot"
) + 
  
  theme_bw()

We note that children’s height is correlated with that of father and mother. The correlations are both positive, and that with father seems to be the larger of the two. ( Look at the slopes of the lines and the values of the correlation scores. )

Question

What if we group the Quant variables based on a Qual variable, like sex of the child?

# Pulling out the list of Quant variables from NHANES
galton_quant <- galton_describe$quantitative
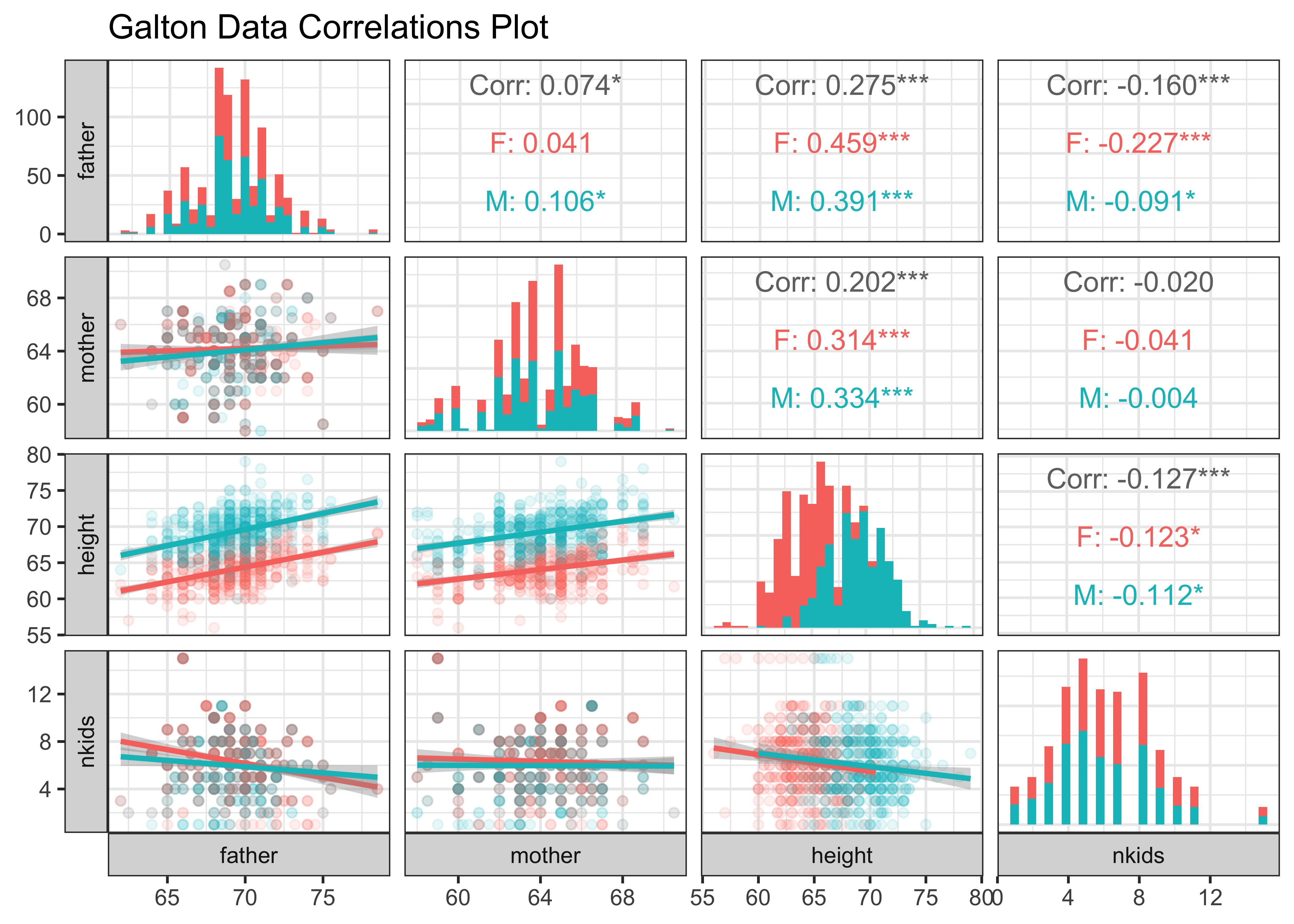
galton_quant$name

[1] "father" "mother" "height" "nkids"

GGally::ggpairs(
  Galton,
  
  mapping = aes(colour = sex), # Colour by `sex`

  # Choose the variables we want to plot for
  columns = c("father", "mother", "height", "nkids"),
  switch = "both", # axis labels in more traditional locations
  progress = FALSE, # no compute progress messages needed
  
  diag = list(continuous = "barDiag"),
  
  # Choose lower triangle graphs, two-variable graphs
  lower = list(continuous = wrap("smooth", alpha = 0.1)),
  
  title = "Galton Data Correlations Plot"
) + 
  
  theme_bw()

The split scatter plots are useful, as is the split histogram for height: Clearly the correlation of children’s height with father and mother is positive for both sex-es. The other plots, and even some of the correlations scores are not all useful! Just shows everything we can compute is not necessarily useful immediately.

In later modules we will see how to plot correlations when the number of variables is larger still.

Question

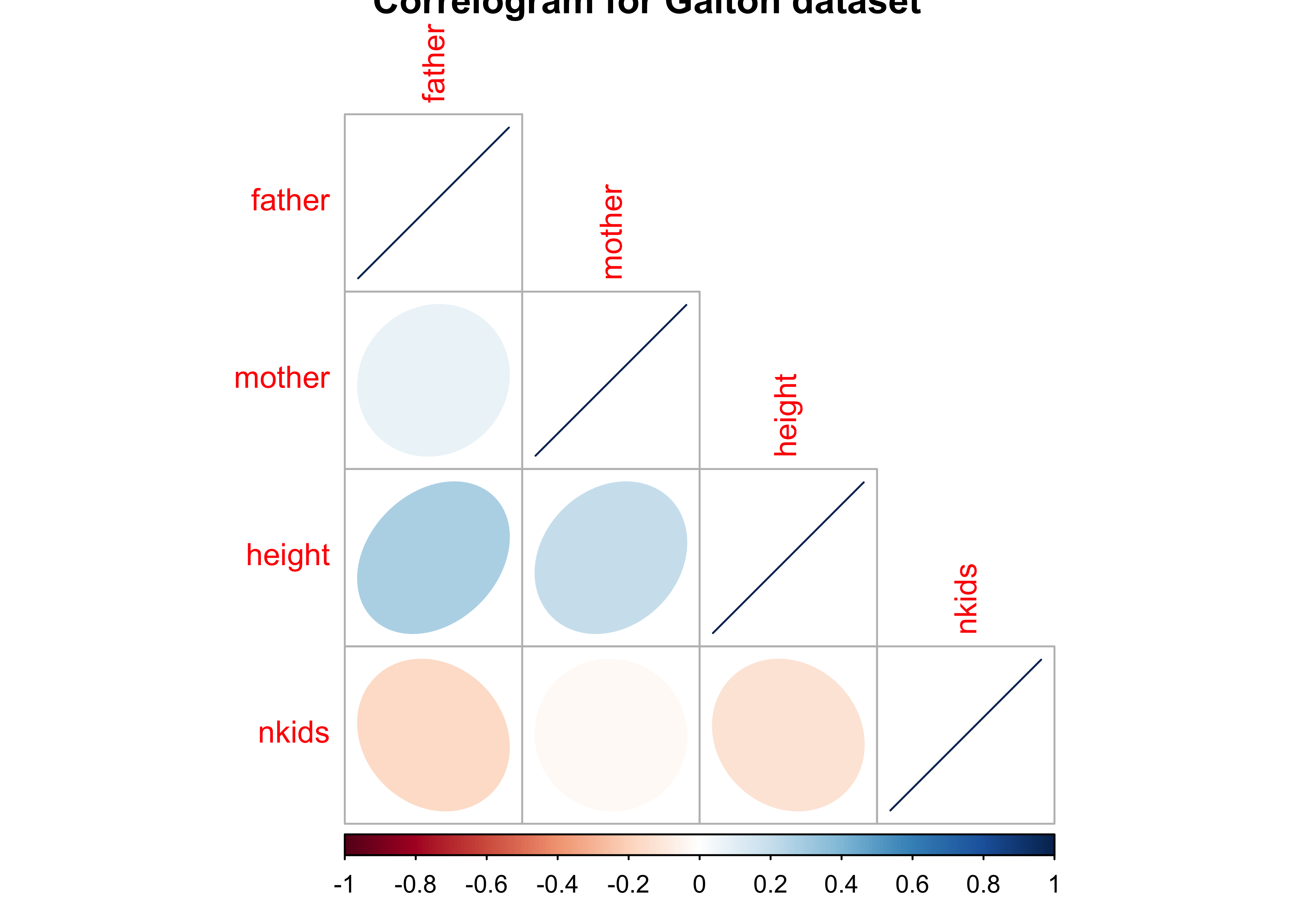
Can we plot a Correlogram for this dataset?

#library(corrplot)

galton_num_var <- Galton %>% select(father, mother, height, nkids)
galton_cor <- cor(galton_num_var)
galton_cor %>%
  corrplot(method = "ellipse",
           type = "lower",
           main = "Correlogram for Galton dataset")

Clearly height is positively correlated to father and mother; interestingly, height is negatively correlated ( slightly) with nkids.

Question

Let us confirm with a correlation test:

We will use the mosaic function cor_test to get these results:

mosaic::cor_test(height ~ father, data = Galton) %>% 
  broom::tidy() %>% 
  knitr::kable(digits = 2,
               caption = "Children vs Fathers")

Children vs Fathers
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.28	8.57	0	896	0.21	0.33	Pearson’s product-moment correlation	two.sided

mosaic::cor_test(height ~ mother, data = Galton) %>% 
  broom::tidy() %>% 
    knitr::kable(digits = 2,
               caption = "Children vs Mothers")

Children vs Mothers
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.2	6.16	0	896	0.14	0.26	Pearson’s product-moment correlation	two.sided

Correlation Scores and Uncertainty

Note how the mosaic::cor_test() reports a correlation score estimate and the p-value for the same. There is also a confidence interval reported for the correlation score, an interval within which we are 95% sure that the true correlation value is to be found.

Note that GGally::ggpairs() too reports the significance of the correlation scores estimates using *** or **. This indicates the p-value in the scores obtained by GGally; Presumably, there is an internal cor_test that is run for each pair of variables and the p-value and confidence levels are also computed internally.

In both cases, we used the formula $h e i g h t \sim o t h e r - v a r i a b l e$ , in keeping with our idea of height being the dependent, target variable..

We also see the p.value for the estimateed correlation is negligible, and the conf.low/conf.high interval does not straddle $0$ . These attest to the significance of the correlation score.

Question

What does this correlation look when split by sex of Child?

# For the sons

mosaic::cor_test(height ~ father,
                 data = Galton %>% filter(sex == "M")) %>% 
  broom::tidy() %>% knitr::kable(digits = 2,
                                 caption = "Sons vs Fathers")
cor_test(height ~ mother, 
         data = Galton %>% filter(sex == "M")) %>% 
  broom::tidy() %>% knitr::kable(digits = 2,
                                 caption = "Sons vs Mothers")

# For the daughters
cor_test(height ~ father, 
         data = Galton %>% filter(sex == "F")) %>% 
  broom::tidy() %>% knitr::kable(digits = 2,
                                 caption = "Daughters vs Fathers")
cor_test(height ~ mother, 
         data = Galton %>% filter(sex == "F")) %>% 
  broom::tidy() %>% knitr::kable(digits = 2,
                                 caption = "Daughters vs Mothers")

Sons vs Fathers
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.39	9.15	0	463	0.31	0.47	Pearson’s product-moment correlation	two.sided

Sons vs Mothers
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.33	7.63	0	463	0.25	0.41	Pearson’s product-moment correlation	two.sided

Daughters vs Fathers
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.46	10.72	0	431	0.38	0.53	Pearson’s product-moment correlation	two.sided

Daughters vs Mothers
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.31	6.86	0	431	0.23	0.4	Pearson’s product-moment correlation	two.sided

The same observation as made above ( p.value and confidence intervals) applies here too and tells us that the estimated correlations are significant.

Visualizing Uncertainty in Correlation Estimates

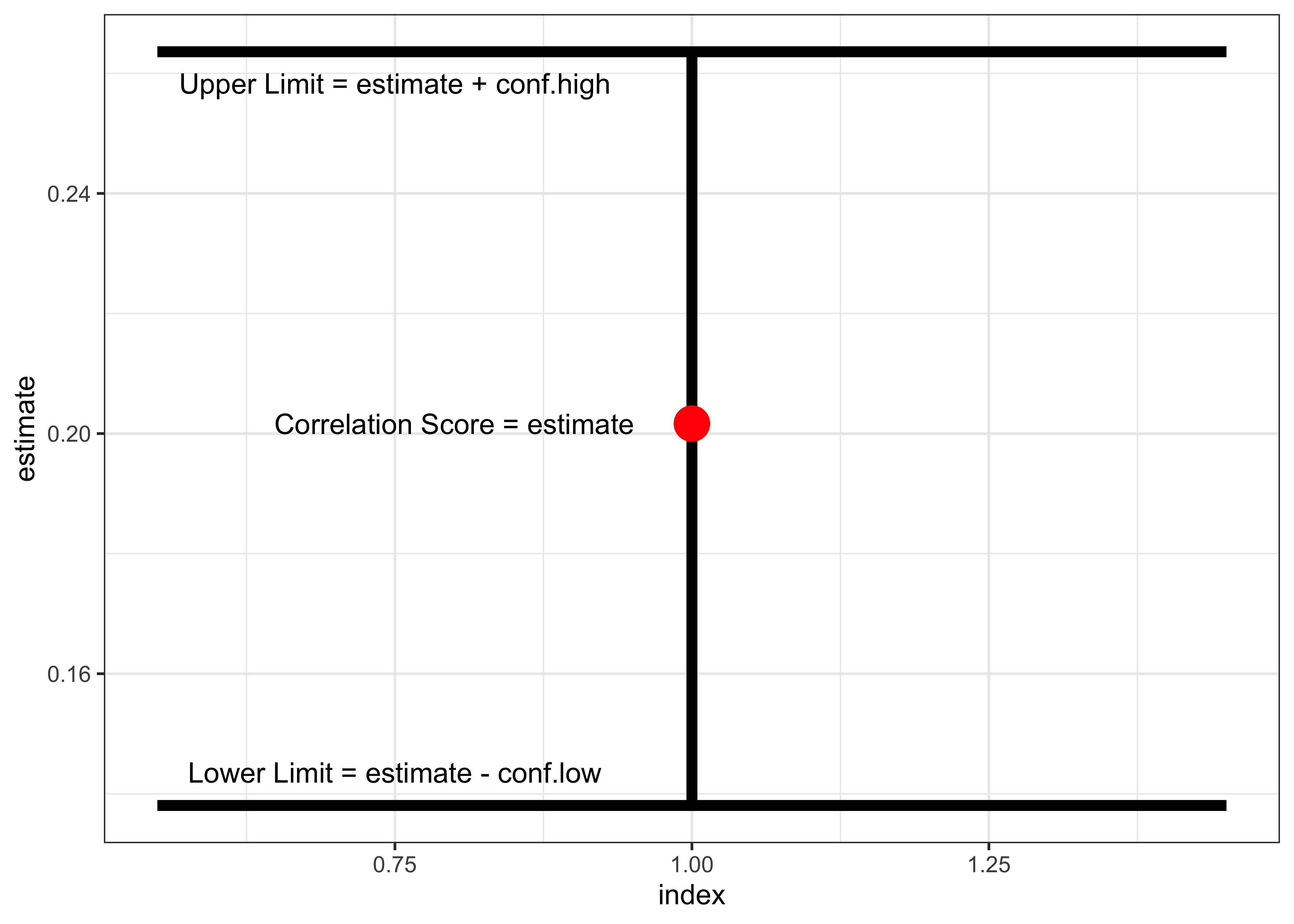
We can also visualize this uncertainty and the confidence levels in a plot too, using gf_errorbar and a handy set of functions within purrr which is part of the tidyverse. Assuming heights is the target variable we want to correlate every other (quantitative) variable against, we can proceed very quickly as follows: we will first plot correlation uncertainty for one pair of variables to develop the intuition, and then for all variables against the one target variable:

mosaic::cor_test(height ~ mother, data = Galton) %>% 
  broom::tidy() %>% 

# We need a graph not a table 
# So comment out this line from the earlier code
#knitr::kable(digits = 2,caption = "Children vs Mothers")

rowid_to_column(var = "index") %>% # Need an index to plot with
  
  # Uncertainty as error-bars
  gf_errorbar(conf.high + conf.low ~ index, linewidth = 2) %>% 
  
  # Estimate as a point
  gf_point(estimate ~ index, color = "red", size = 6) %>% 
  
  # Labels
  gf_text(estimate ~ index - 0.2, 
             label = "Correlation Score = estimate") %>% 
  gf_text(conf.high*0.98 ~ index - 0.25, 
           label = "Upper Limit = estimate + conf.high") %>%   
  gf_text(conf.low*1.04 ~ index - 0.25, 
           label = "Lower Limit = estimate - conf.low") %>% 
  gf_theme(theme_bw())

We can now do this for all variables against the target variable height, which we identified in our research question. We will use the iteration capabilities offered by the tidyverse package, purrr:

all_corrs <- Galton %>% 
  select(where(is.numeric)) %>% 
  
  # leave off height to get all the remaining ones
  select(- height) %>%  
  
  # perform a cor.test for all variables against height
  purrr::map(.x = .,
             .f = \(x) cor.test(x, Galton$height)) %>%
  
  # tidy up the cor.test outputs into a tidy data frame
  map_dfr(broom::tidy, .id = "predictor") 

all_corrs

ABCDEFGHIJ0123456789

predictor <chr>	estimate <dbl>	statistic <dbl>	p.value <dbl>	parameter <int>	conf.low <dbl>	conf.high <dbl>
father	0.2753548	8.573704	4.354588e-17	896	0.2137851	0.33474554
mother	0.2016549	6.162793	1.079105e-09	896	0.1380554	0.26359819
nkids	-0.1269101	-3.829800	1.371780e-04	896	-0.1907472	-0.06200411

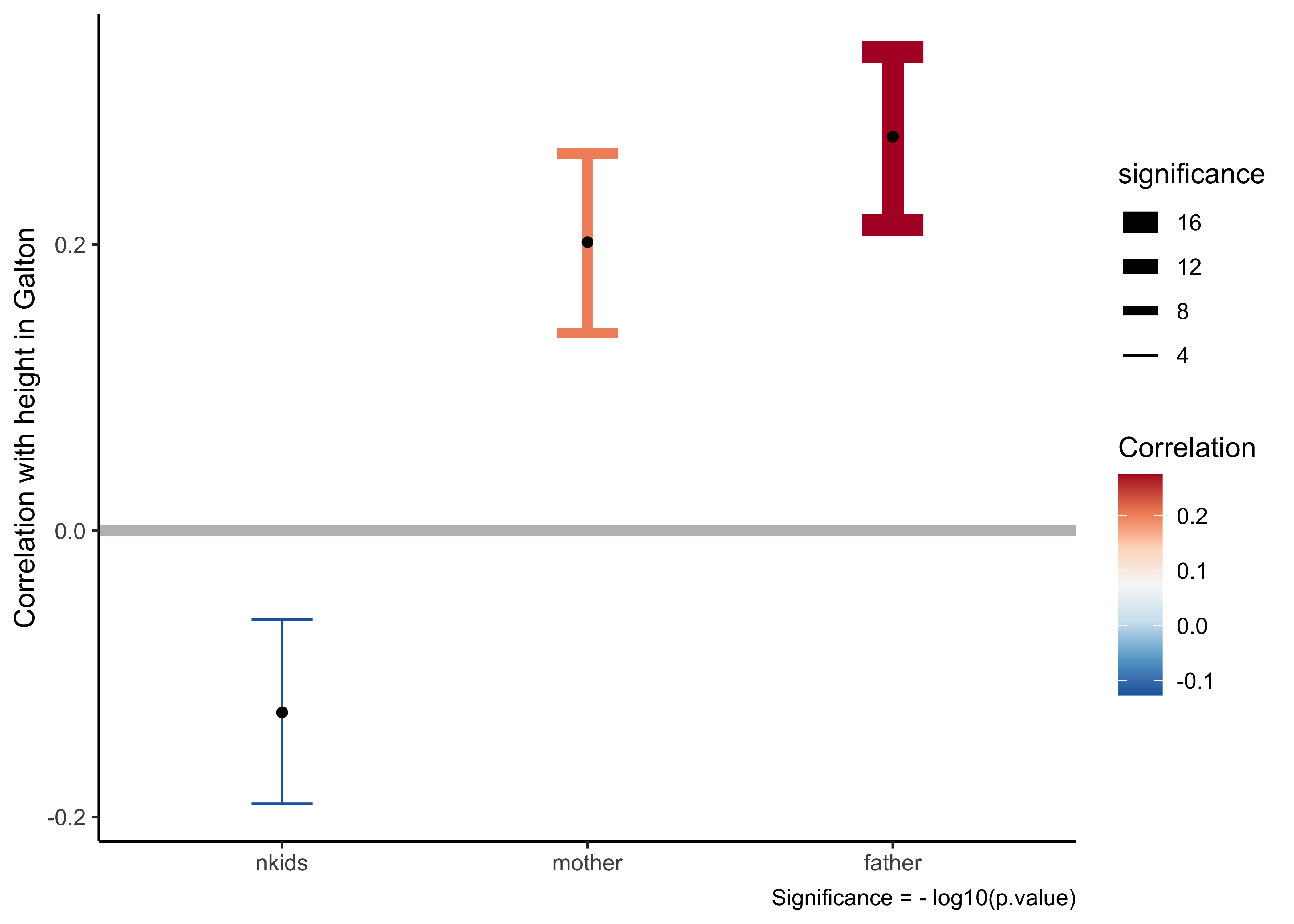
all_corrs %>% 
  
  # arrange the predictors in order of their correlation scores
  # with the target variable (`height`)
  # Add errorbars to show uncertainty ranges / confidence intervals
  # Use errorbar width and linewidth fo emphasis
  gf_errorbar(conf.high + conf.low ~ reorder(predictor, estimate),
              color = ~ estimate,
              width = 0.2,
              linewidth = ~ -log10(p.value)) %>% 
  
  # All correlation estimates as points
  gf_point(estimate ~ reorder(predictor, estimate), 
           color = "black") %>% 
  
  # Reference line at zero correlation score
  gf_hline(yintercept = 0, color = "grey", linewidth = 2) %>% 
  
  # Themes,Titles, and Scales
  gf_labs(x = NULL, y = "Correlation with height in Galton", 
          caption = "Significance = - log10(p.value)") %>% 
  
  gf_refine(
    
    # Scale for colour
 scale_colour_distiller("Correlation", type = "div", palette = "RdBu"),
            
    # Scale for dumbbells!!
    scale_linewidth_continuous("significance",
                                       range = c(0.5,4))) %>% 
  gf_refine(guides(linewidth = guide_legend(reverse = TRUE))) %>%
  gf_theme(theme_classic())

We can clearly see the size of the correlations and the confidence intervals marked in this plot. father has somewhat greater correlation with children’s height, as compared to mother. nkids seems to matter very little. This kind of plot will be very useful when we pursue linear regression models.

Question

How can we show this correlation in a set of Scatter Plots + Regression Lines? Can we recreate Galton’s famous diagram?

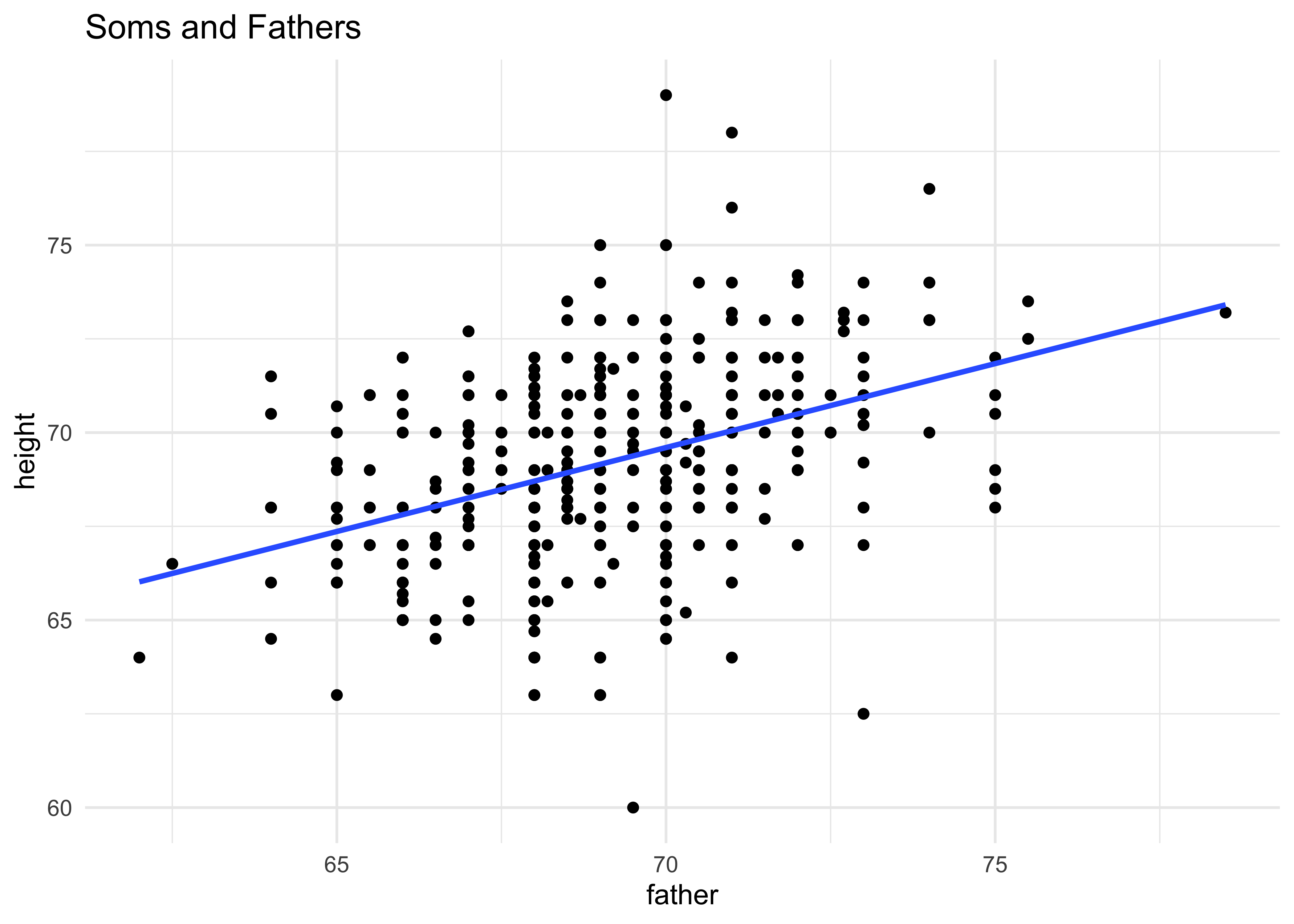
# For the sons
gf_point(height ~ father, 
         data = Galton %>% filter(sex == "M"),
         title = "Soms and Fathers") %>%
  gf_smooth(method = "lm") %>%
  gf_theme(theme_minimal())
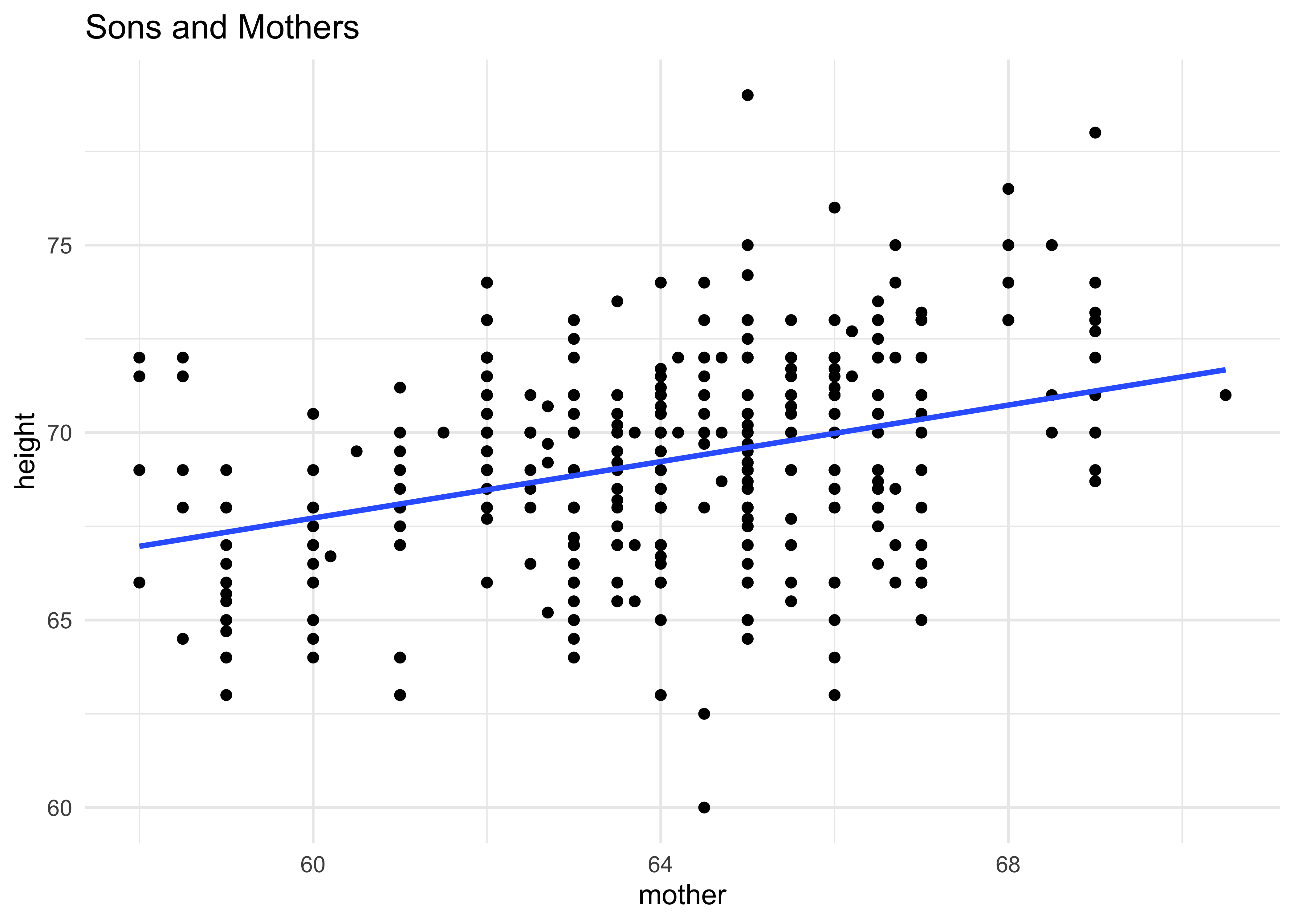
gf_point(height ~ mother, 
         data = Galton %>% filter(sex == "M"),
         title = "Sons and Mothers") %>%
  gf_smooth(method = "lm") %>%
  gf_theme(theme_minimal())
# For the daughters
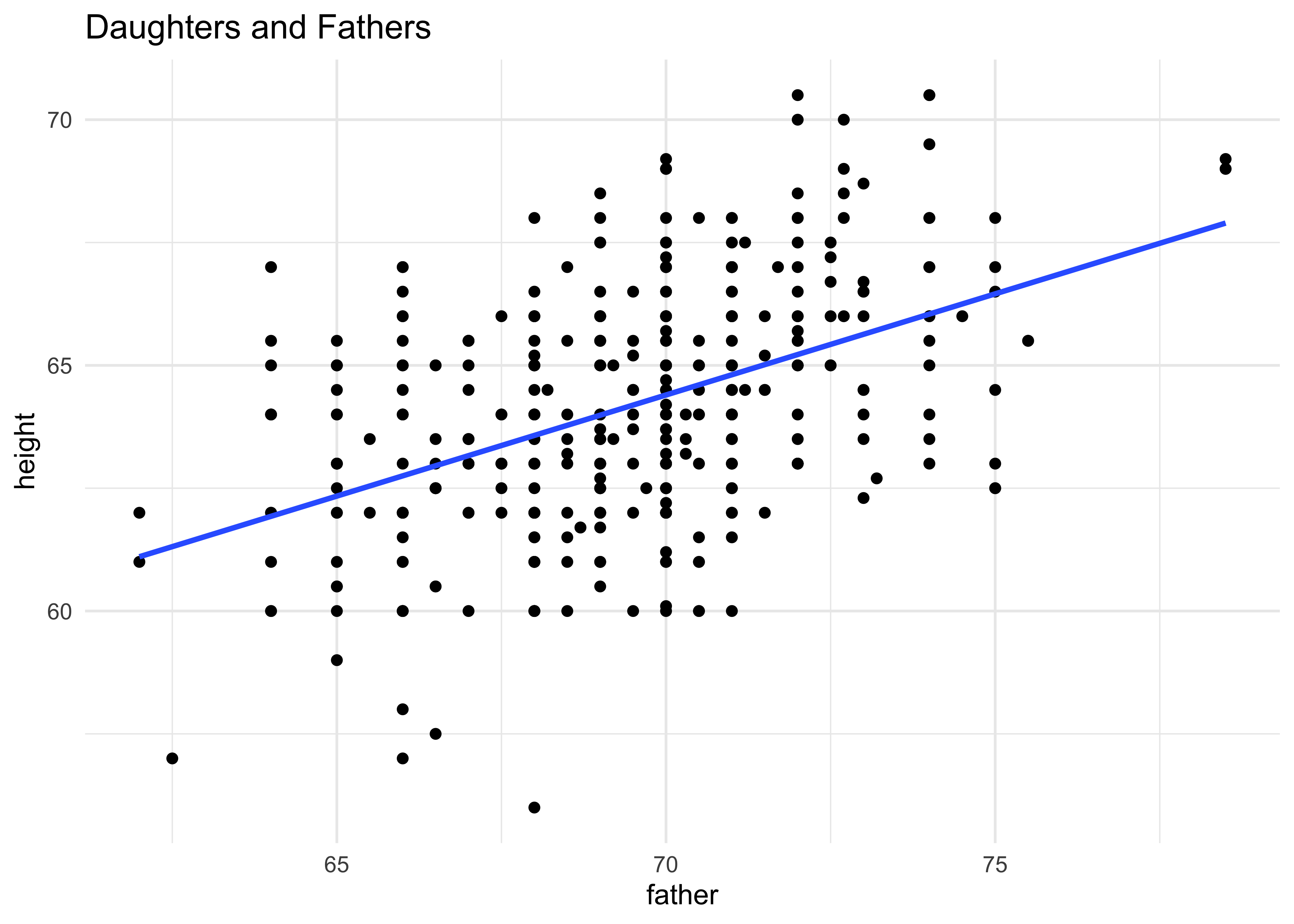
gf_point(height ~ father, 
         data = Galton %>% filter(sex == "F"),
         title = "Daughters and Fathers") %>%
  gf_smooth(method = "lm") %>%
  gf_theme(theme_minimal())
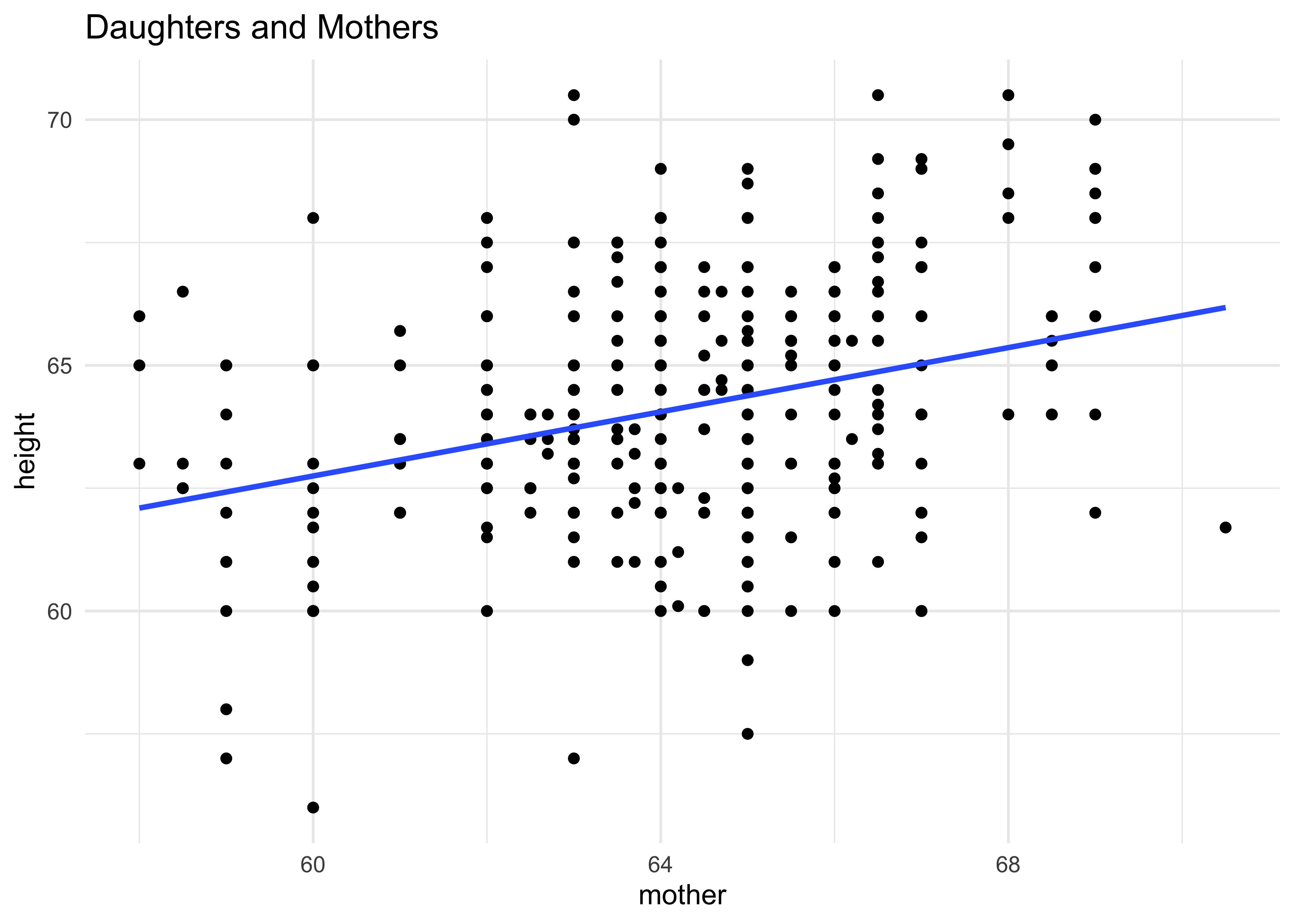
gf_point(height ~ mother, 
         data = Galton %>% filter(sex == "F"),
         title = "Daughters and Mothers") %>%
  gf_smooth(method = "lm") %>% 
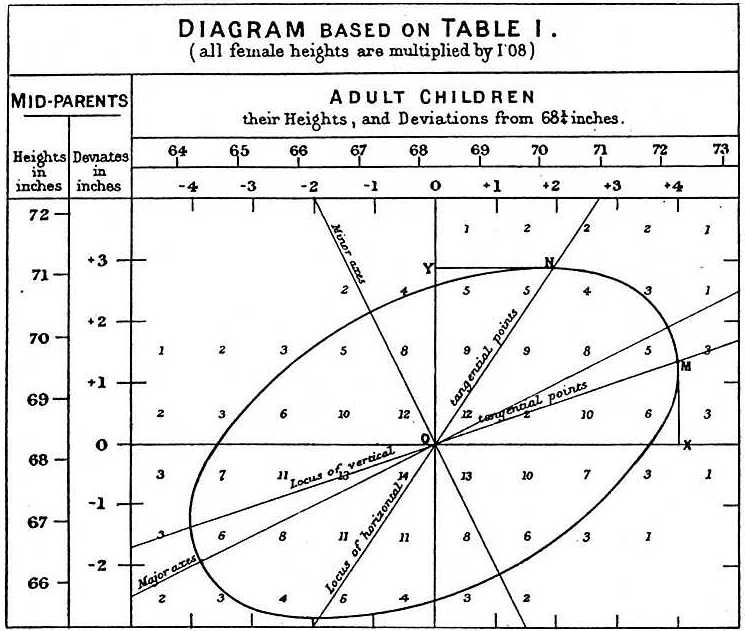
  gf_theme(theme_minimal())

An approximation to Galton’s famous plot¹ (see Wikipedia):

gf_point(height ~ (father + mother)/2, data = Galton) %>% 
  gf_smooth(method = "lm") %>% 
  gf_density_2d(n = 8) %>% 
  gf_abline(slope = 1) %>% 
  gf_theme(theme_minimal())
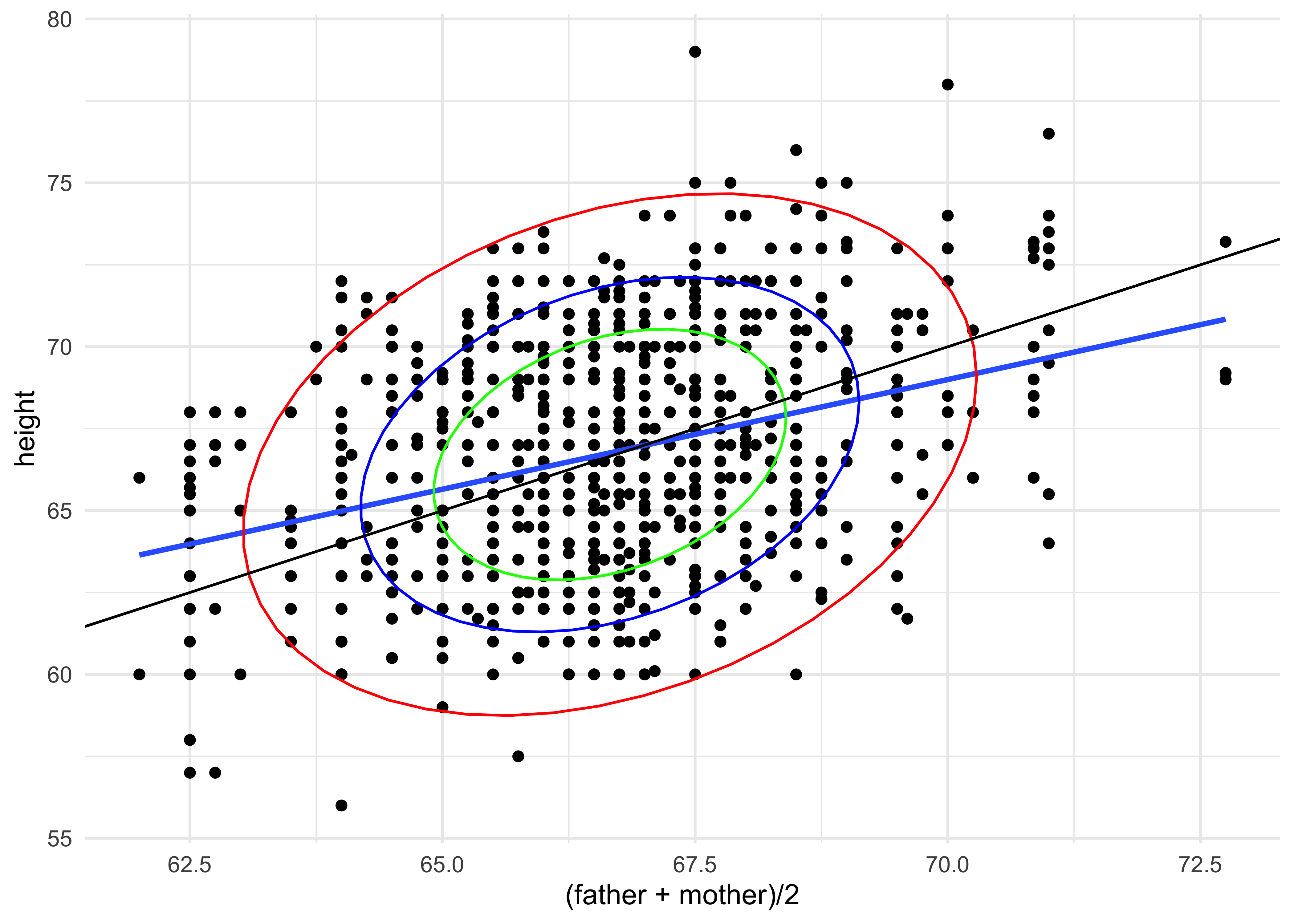
gf_point(height ~ (father + mother)/2, data = Galton) %>% 
  gf_smooth(method = "lm") %>% 
  gf_ellipse(level = 0.95, color = "red") %>% 
    gf_ellipse(level = 0.75, color = "blue") %>% 
    gf_ellipse(level = 0.5, color = "green") %>% 
  gf_abline(slope = 1) %>% 
  gf_theme(theme_minimal())

How would you interpret this plot²?

Case Study#2: Dataset from `NHANES`

Let us look at the NHANES dataset from the package NHANES:

data("NHANES")

Inspecting the Data

NHANES_describe <- inspect(NHANES)

NHANES_describe$categorical
NHANES_describe$quantitative
NHANES
skimr::skim(NHANES)

ABCDEFGHIJ0123456789

name <chr>	class <chr>	levels <int>
SurveyYr	factor	2
Gender	factor	2
AgeDecade	factor	8
Race1	factor	5
Race3	factor	6
Education	factor	5
MaritalStatus	factor	6
HHIncome	factor	12
HomeOwn	factor	3
Work	factor	3

ABCDEFGHIJ0123456789

	name <chr>	class <chr>
1	ID	integer
2	Age	integer
3	AgeMonths	integer
4	HHIncomeMid	integer
5	Poverty	numeric
6	HomeRooms	integer
7	Weight	numeric
8	Length	numeric
9	HeadCirc	numeric
10	Height	numeric

ABCDEFGHIJ0123456789

ID <int>	SurveyYr <fct>	Gender <fct>	Age <int>
51624	2009_10	male	34
51624	2009_10	male	34
51624	2009_10	male	34
51625	2009_10	male	4
51630	2009_10	female	49
51638	2009_10	male	9
51646	2009_10	male	8
51647	2009_10	female	45
51647	2009_10	female	45
51647	2009_10	female	45

Data summary
Name	NHANES
Number of rows	10000
Number of columns	76
_______________________
Column type frequency:
factor	31
numeric	45
________________________
Group variables	None

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
SurveyYr	0	1.00	FALSE	2	200: 5000, 201: 5000
Gender	0	1.00	FALSE	2	fem: 5020, mal: 4980
AgeDecade	333	0.97	FALSE	8	40: 1398, 0-: 1391, 10: 1374, 20: 1356
Race1	0	1.00	FALSE	5	Whi: 6372, Bla: 1197, Mex: 1015, Oth: 806
Race3	5000	0.50	FALSE	6	Whi: 3135, Bla: 589, Mex: 480, His: 350
Education	2779	0.72	FALSE	5	Som: 2267, Col: 2098, Hig: 1517, 9 -: 888
MaritalStatus	2769	0.72	FALSE	6	Mar: 3945, Nev: 1380, Div: 707, Liv: 560
HHIncome	811	0.92	FALSE	12	mor: 2220, 750: 1084, 250: 958, 350: 863
HomeOwn	63	0.99	FALSE	3	Own: 6425, Ren: 3287, Oth: 225
Work	2229	0.78	FALSE	3	Wor: 4613, Not: 2847, Loo: 311
BMICatUnder20yrs	8726	0.13	FALSE	4	Nor: 805, Obe: 221, Ove: 193, Und: 55
BMI_WHO	397	0.96	FALSE	4	18.: 2911, 30.: 2751, 25.: 2664, 12.: 1277
Diabetes	142	0.99	FALSE	2	No: 9098, Yes: 760
HealthGen	2461	0.75	FALSE	5	Goo: 2956, Vgo: 2508, Fai: 1010, Exc: 878
LittleInterest	3333	0.67	FALSE	3	Non: 5103, Sev: 1130, Mos: 434
Depressed	3327	0.67	FALSE	3	Non: 5246, Sev: 1009, Mos: 418
SleepTrouble	2228	0.78	FALSE	2	No: 5799, Yes: 1973
PhysActive	1674	0.83	FALSE	2	Yes: 4649, No: 3677
TVHrsDay	5141	0.49	FALSE	7	2_h: 1275, 1_h: 884, 3_h: 836, 0_t: 638
CompHrsDay	5137	0.49	FALSE	7	0_t: 1409, 0_h: 1073, 1_h: 1030, 2_h: 589
Alcohol12PlusYr	3420	0.66	FALSE	2	Yes: 5212, No: 1368
SmokeNow	6789	0.32	FALSE	2	No: 1745, Yes: 1466
Smoke100	2765	0.72	FALSE	2	No: 4024, Yes: 3211
Smoke100n	2765	0.72	FALSE	2	Non: 4024, Smo: 3211
Marijuana	5059	0.49	FALSE	2	Yes: 2892, No: 2049
RegularMarij	5059	0.49	FALSE	2	No: 3575, Yes: 1366
HardDrugs	4235	0.58	FALSE	2	No: 4700, Yes: 1065
SexEver	4233	0.58	FALSE	2	Yes: 5544, No: 223
SameSex	4232	0.58	FALSE	2	No: 5353, Yes: 415
SexOrientation	5158	0.48	FALSE	3	Het: 4638, Bis: 119, Hom: 85
PregnantNow	8304	0.17	FALSE	3	No: 1573, Yes: 72, Unk: 51

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
ID	0	1.00	61944.64	5871.17	51624.00	56904.50	62159.50	67039.00	71915.00	▇▇▇▇▇
Age	0	1.00	36.74	22.40	0.00	17.00	36.00	54.00	80.00	▇▇▇▆▅
AgeMonths	5038	0.50	420.12	259.04	0.00	199.00	418.00	624.00	959.00	▇▇▇▆▃
HHIncomeMid	811	0.92	57206.17	33020.28	2500.00	30000.00	50000.00	87500.00	100000.00	▃▆▃▁▇
Poverty	726	0.93	2.80	1.68	0.00	1.24	2.70	4.71	5.00	▅▅▃▃▇
HomeRooms	69	0.99	6.25	2.28	1.00	5.00	6.00	8.00	13.00	▂▆▇▂▁
Weight	78	0.99	70.98	29.13	2.80	56.10	72.70	88.90	230.70	▂▇▂▁▁
Length	9457	0.05	85.02	13.71	47.10	75.70	87.00	96.10	112.20	▁▃▆▇▃
HeadCirc	9912	0.01	41.18	2.31	34.20	39.58	41.45	42.92	45.40	▁▂▇▇▅
Height	353	0.96	161.88	20.19	83.60	156.80	166.00	174.50	200.40	▁▁▁▇▂
BMI	366	0.96	26.66	7.38	12.88	21.58	25.98	30.89	81.25	▇▆▁▁▁
Pulse	1437	0.86	73.56	12.16	40.00	64.00	72.00	82.00	136.00	▂▇▃▁▁
BPSysAve	1449	0.86	118.15	17.25	76.00	106.00	116.00	127.00	226.00	▃▇▂▁▁
BPDiaAve	1449	0.86	67.48	14.35	0.00	61.00	69.00	76.00	116.00	▁▁▇▇▁
BPSys1	1763	0.82	119.09	17.50	72.00	106.00	116.00	128.00	232.00	▂▇▂▁▁
BPDia1	1763	0.82	68.28	13.78	0.00	62.00	70.00	76.00	118.00	▁▁▇▆▁
BPSys2	1647	0.84	118.48	17.49	76.00	106.00	116.00	128.00	226.00	▃▇▂▁▁
BPDia2	1647	0.84	67.66	14.42	0.00	60.00	68.00	76.00	118.00	▁▁▇▆▁
BPSys3	1635	0.84	117.93	17.18	76.00	106.00	116.00	126.00	226.00	▃▇▂▁▁
BPDia3	1635	0.84	67.30	14.96	0.00	60.00	68.00	76.00	116.00	▁▁▇▇▁
Testosterone	5874	0.41	197.90	226.50	0.25	17.70	43.82	362.41	1795.60	▇▂▁▁▁
DirectChol	1526	0.85	1.36	0.40	0.39	1.09	1.29	1.58	4.03	▅▇▂▁▁
TotChol	1526	0.85	4.88	1.08	1.53	4.11	4.78	5.53	13.65	▂▇▁▁▁
UrineVol1	987	0.90	118.52	90.34	0.00	50.00	94.00	164.00	510.00	▇▅▂▁▁
UrineFlow1	1603	0.84	0.98	0.95	0.00	0.40	0.70	1.22	17.17	▇▁▁▁▁
UrineVol2	8522	0.15	119.68	90.16	0.00	52.00	95.00	171.75	409.00	▇▆▃▂▁
UrineFlow2	8524	0.15	1.15	1.07	0.00	0.48	0.76	1.51	13.69	▇▁▁▁▁
DiabetesAge	9371	0.06	48.42	15.68	1.00	40.00	50.00	58.00	80.00	▁▂▆▇▂
DaysPhysHlthBad	2468	0.75	3.33	7.40	0.00	0.00	0.00	3.00	30.00	▇▁▁▁▁
DaysMentHlthBad	2466	0.75	4.13	7.83	0.00	0.00	0.00	4.00	30.00	▇▁▁▁▁
nPregnancies	7396	0.26	3.03	1.80	1.00	2.00	3.00	4.00	32.00	▇▁▁▁▁
nBabies	7584	0.24	2.46	1.32	0.00	2.00	2.00	3.00	12.00	▇▅▁▁▁
Age1stBaby	8116	0.19	22.65	4.77	14.00	19.00	22.00	26.00	39.00	▆▇▅▂▁
SleepHrsNight	2245	0.78	6.93	1.35	2.00	6.00	7.00	8.00	12.00	▁▅▇▁▁
PhysActiveDays	5337	0.47	3.74	1.84	1.00	2.00	3.00	5.00	7.00	▇▇▃▅▅
TVHrsDayChild	9347	0.07	1.94	1.43	0.00	1.00	2.00	3.00	6.00	▇▆▂▂▂
CompHrsDayChild	9347	0.07	2.20	2.52	0.00	0.00	1.00	6.00	6.00	▇▁▁▁▃
AlcoholDay	5086	0.49	2.91	3.18	1.00	1.00	2.00	3.00	82.00	▇▁▁▁▁
AlcoholYear	4078	0.59	75.10	103.03	0.00	3.00	24.00	104.00	364.00	▇▁▁▁▁
SmokeAge	6920	0.31	17.83	5.33	6.00	15.00	17.00	19.00	72.00	▇▂▁▁▁
AgeFirstMarij	7109	0.29	17.02	3.90	1.00	15.00	16.00	19.00	48.00	▁▇▂▁▁
AgeRegMarij	8634	0.14	17.69	4.81	5.00	15.00	17.00	19.00	52.00	▂▇▁▁▁
SexAge	4460	0.55	17.43	3.72	9.00	15.00	17.00	19.00	50.00	▇▅▁▁▁
SexNumPartnLife	4275	0.57	15.09	57.85	0.00	2.00	5.00	12.00	2000.00	▇▁▁▁▁
SexNumPartYear	5072	0.49	1.34	2.78	0.00	1.00	1.00	1.00	69.00	▇▁▁▁▁

Try help("NHANES") in your Console.

This is survey data collected by the US National Center for Health Statistics (NCHS) which has conducted a series of health and nutrition surveys since the early 1960’s. Since 1999 approximately 5,000 individuals of all ages are interviewed in their homes every year and complete the health examination component of the survey. The health examination is conducted in a mobile examination centre (MEC).

The dataset is described as: A data frame with 100000 observations on 76 variables. Some of these are:
- Race1 and Race2: factors with 5 and 6 levels respectively
- Education a factor with 5 levels
- HHIncomeMid Total annual gross income for the household in US dollars.
- Age
- BMI: Body mass index (weight/height2 in kg/m2)
- Height: Standing height in cm.
- Weight: Weight in kg > > - Testosterone: Testosterone total (ng/dL) - PhysActiveDays: Number of days in a typical week that participant does moderate or vigorous-intensity activity.
- CompHrsDay: Number of hours per day on average participant used a computer or gaming device over the past 30 days.

Missing Data

Why do so many of the variables have missing entries? What could be your guess about the Experiment/Survey`?

Let us make some counts of the data, since we have so many factors:

NHANES %>% count(Gender)

ABCDEFGHIJ0123456789

Gender <fct>	n <int>
female	5020
male	4980

NHANES %>% count(Race1)

ABCDEFGHIJ0123456789

Race1 <fct>	n <int>
Black	1197
Hispanic	610
Mexican	1015
White	6372
Other	806

NHANES %>% count(Race3)

ABCDEFGHIJ0123456789

Race3 <fct>	n <int>
Asian	288
Black	589
Hispanic	350
Mexican	480
White	3135
Other	158
NA	5000

NHANES %>% count(Education)

ABCDEFGHIJ0123456789

Education <fct>	n <int>
8th Grade	451
9 - 11th Grade	888
High School	1517
Some College	2267
College Grad	2098
NA	2779

NHANES %>% count(MaritalStatus)

ABCDEFGHIJ0123456789

MaritalStatus <fct>	n <int>
Divorced	707
LivePartner	560
Married	3945
NeverMarried	1380
Separated	183
Widowed	456
NA	2769

There is a good mix of factors and counts.

Now we articulate our Research Questions:

Research Questions

Does Testosterone have a relationship with parameters such as BMI, Weight, Height, PhysActiveDays CompHrsDay and Age?
Does HHIncomeMid have a relationship with these same parameters? And with Gender?
Are there any other pairwise correlations that we should note? (This is especially useful in choosing independent variables for multiple regression)

( Yes we are concerned with men more than with the women, sadly.)

Correlations and Plots

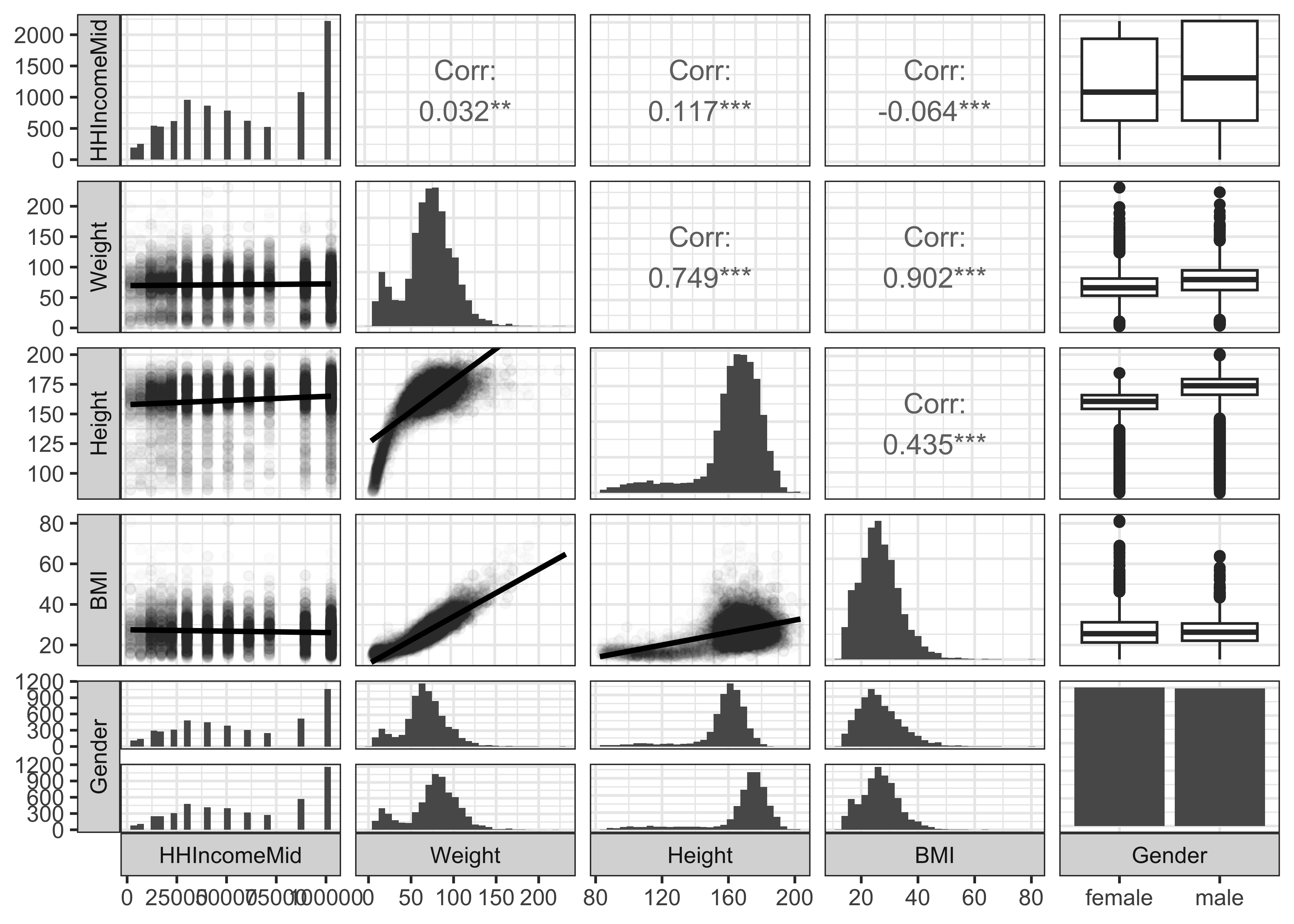
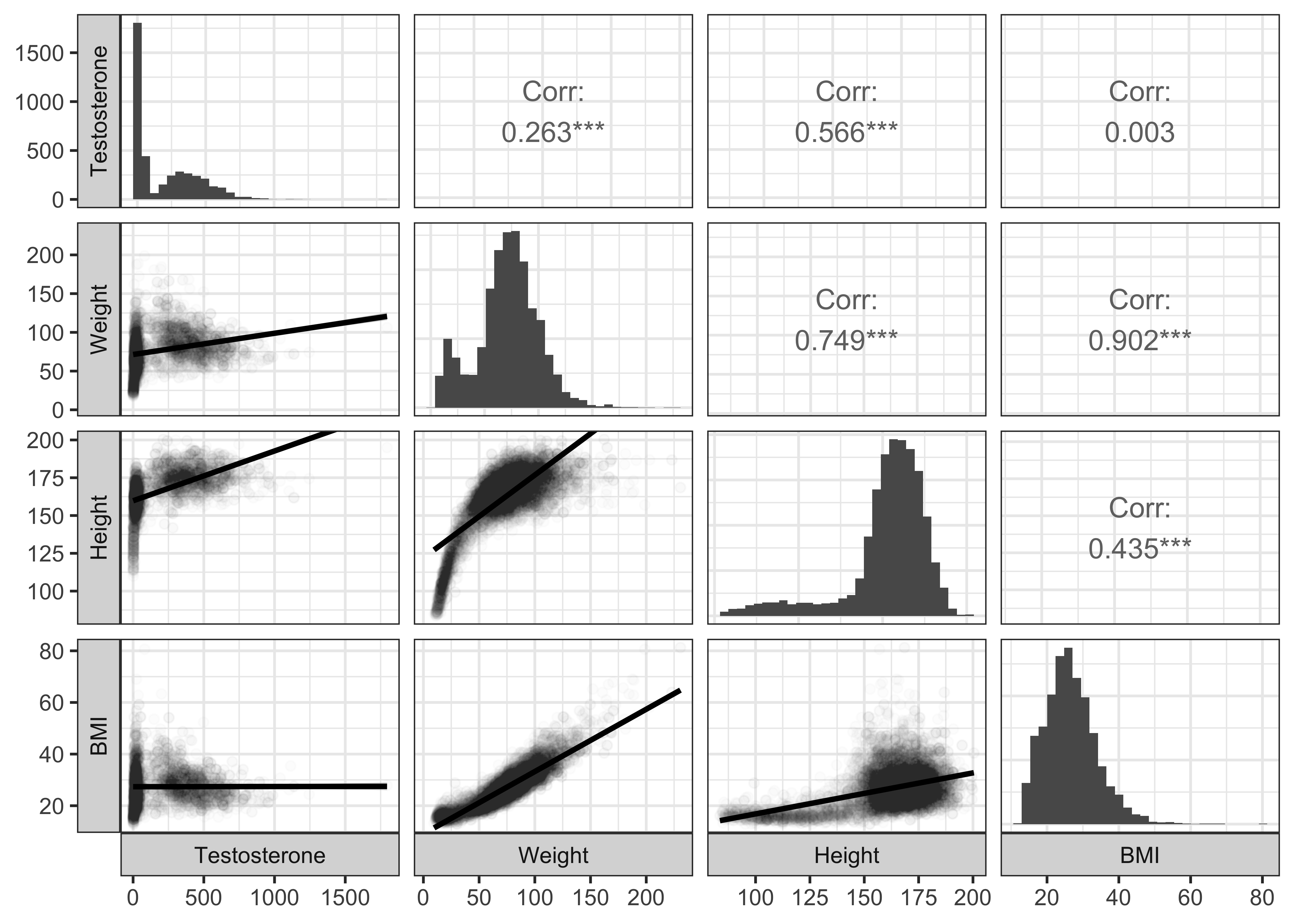
GGally::ggpairs(NHANES, 
                # Choose the variables we want to plot for
                columns = c("HHIncomeMid", "Weight", "Height", 
                            "BMI", "Gender"), 
                
                # LISTs of graphs needed at different locations
                # For different combinations of variables 
                diag = list(continuous = "barDiag"),
                lower = list(continuous = wrap("smooth", alpha = 0.01)),
                upper = list(continuous = "cor"),
                
                switch = "both", # axis labels in more traditional locations
                progress = FALSE ) + # No compute progress bars needed
  theme_bw()

We see that HHIncomeMid is Quantitative, discrete valued variable, since it is based on a set of median incomes for different ranges of income. BMI, Weight, Height are continuous Quant variables.

HHIncomeMid also seems to be relatively unaffected by Weight; And is only mildly correlated with Height and BMI, as seen both by the correlation score magnitudes and the slopes of the trend lines.

There is a difference in the median income by Gender, but we will defer that kind of test for later, when we do Statistical Inference.

Unsurprisingly, BMI and Weight have a strong relationship, as do Height and Weight; the latter is of course non-linear, since the Height levels off at a point.

GGally::ggpairs(NHANES, 
                columns = c("Testosterone", "Weight", "Height", "BMI"), 
                
                diag = list(continuous = "barDiag"),
                lower = list(continuous = wrap("smooth", alpha = 0.01)),
                upper = list(continuous = "cor"),
                
                switch = "both",
                progress = FALSE ) +
  theme_bw()

It is clear that Testosterone has strong relationships with Height and Weight but not so much with BMI.

Visualizing Uncertainty in Correlation Estimates

Since the pairs plot is fairly clear for both target variables, let us head to visualizing the significance and uncertainty in the correlation estimates.

HHIncome_corrs <- NHANES %>% 
  select(where(is.numeric)) %>% 
  
  # leave off height to get all the remaining ones
  select(- HHIncomeMid) %>%  
  
  # perform a cor.test for all variables against height
  purrr::map(.x = .,
             .f = \(x) cor.test(x, NHANES$HHIncomeMid)) %>%
  
  # tidy up the cor.test outputs into a tidy data frame
  map_dfr(broom::tidy, .id = "predictor") 

HHIncome_corrs

ABCDEFGHIJ0123456789

predictor <chr>	estimate <dbl>	statistic <dbl>	p.value <dbl>	parameter <int>	conf.low <dbl>	conf.high <dbl>
ID	-0.001803175	-0.17283253	8.627869e-01	9187	-2.224911e-02	0.018644265
Age	0.020381745	1.95397248	5.073477e-02	9187	-6.503467e-05	0.040811489
AgeMonths	0.059212540	3.99232121	6.646547e-05	4530	3.014902e-02	0.088176019
Poverty	0.895687490	192.89158662	0.000000e+00	9171	8.915652e-01	0.899661395
HomeRooms	0.452118084	48.57089131	0.000000e+00	9182	4.356946e-01	0.468240645
Weight	0.032259894	3.08204398	2.061977e-03	9118	1.174371e-02	0.052748927
Length	-0.002611812	-0.05857705	9.533123e-01	503	-8.984636e-02	0.084662501
HeadCirc	0.040561659	0.36081685	7.191994e-01	79	-1.793764e-01	0.256638118
Height	0.116781182	11.06806055	2.745490e-28	8860	9.619449e-02	0.137268008
BMI	-0.063549377	-5.99048053	2.173863e-09	8850	-8.427016e-02	-0.042773659

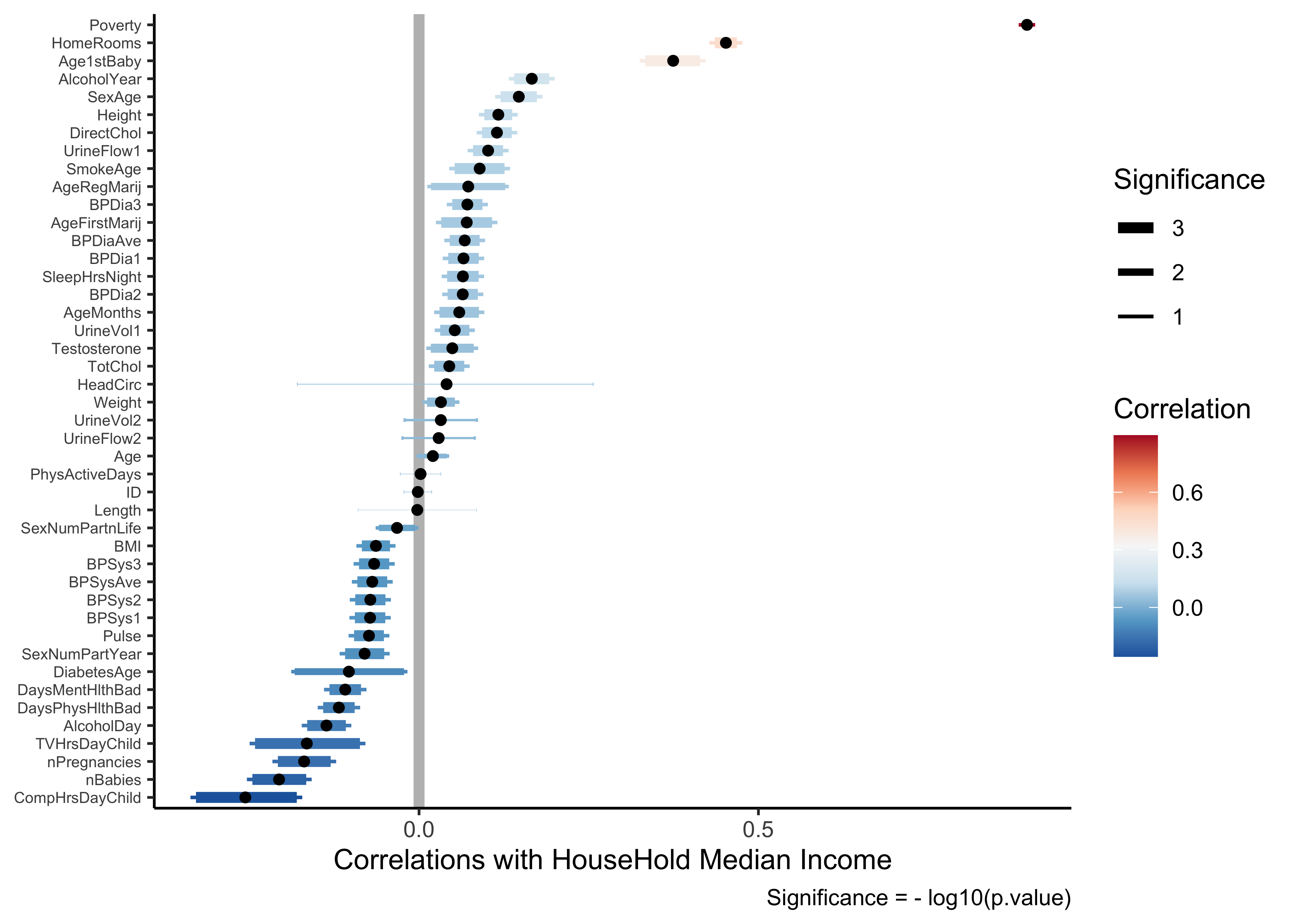
HHIncome_corrs %>% 
  
  # Reference line at zero correlation score
  gf_hline(yintercept = 0, color = "grey", linewidth = 2) %>% 
  
  # arrange the predictors in order of their correlation scores
  # with the target variable (`height`)
  # Add errorbars to show uncertainty ranges / confidence intervals
  # Use errorbar width and linewidth fo emphasis
  gf_errorbar(conf.high + conf.low ~ reorder(predictor, estimate),
              color = ~ estimate,
              width = 0.2,
              linewidth = ~ -log10(p.value + 0.001)) %>% 
  
  # All correlation estimates as points
  gf_point(estimate ~ reorder(predictor, estimate), 
           color = "black") %>% 
  
  # Themes,Titles, and Scales
  gf_labs(x = NULL, y = "Correlations with HouseHold Median Income", 
          caption = "Significance = - log10(p.value)") %>% 
  gf_theme(theme_classic()) %>%

  
  # Scale for colour
  gf_refine(guides(linewidth = guide_legend(reverse = TRUE)),
            scale_colour_distiller("Correlation", type = "div", 
                                    palette = "RdBu"),
            
  # Scale for dumbbells!!
  scale_linewidth_continuous("Significance", range = c(0.05,2)),
  
  theme(axis.text.y = element_text(size = 6, hjust = 1)),
  coord_flip())

If we select just the variables from our Research Question:

HHIncome_corrs_select <- NHANES %>% 
  select(Height, Weight, BMI) %>% # Only change is here!
  
  # leave off height to get all the remaining ones
  #select(- HHIncomeMid) %>%  
  
  # perform a cor.test for all variables against height
  purrr::map(.x = .,
             .f = \(x) cor.test(x, NHANES$HHIncomeMid)) %>%
  
  # tidy up the cor.test outputs into a tidy data frame
  map_dfr(broom::tidy, .id = "predictor") 

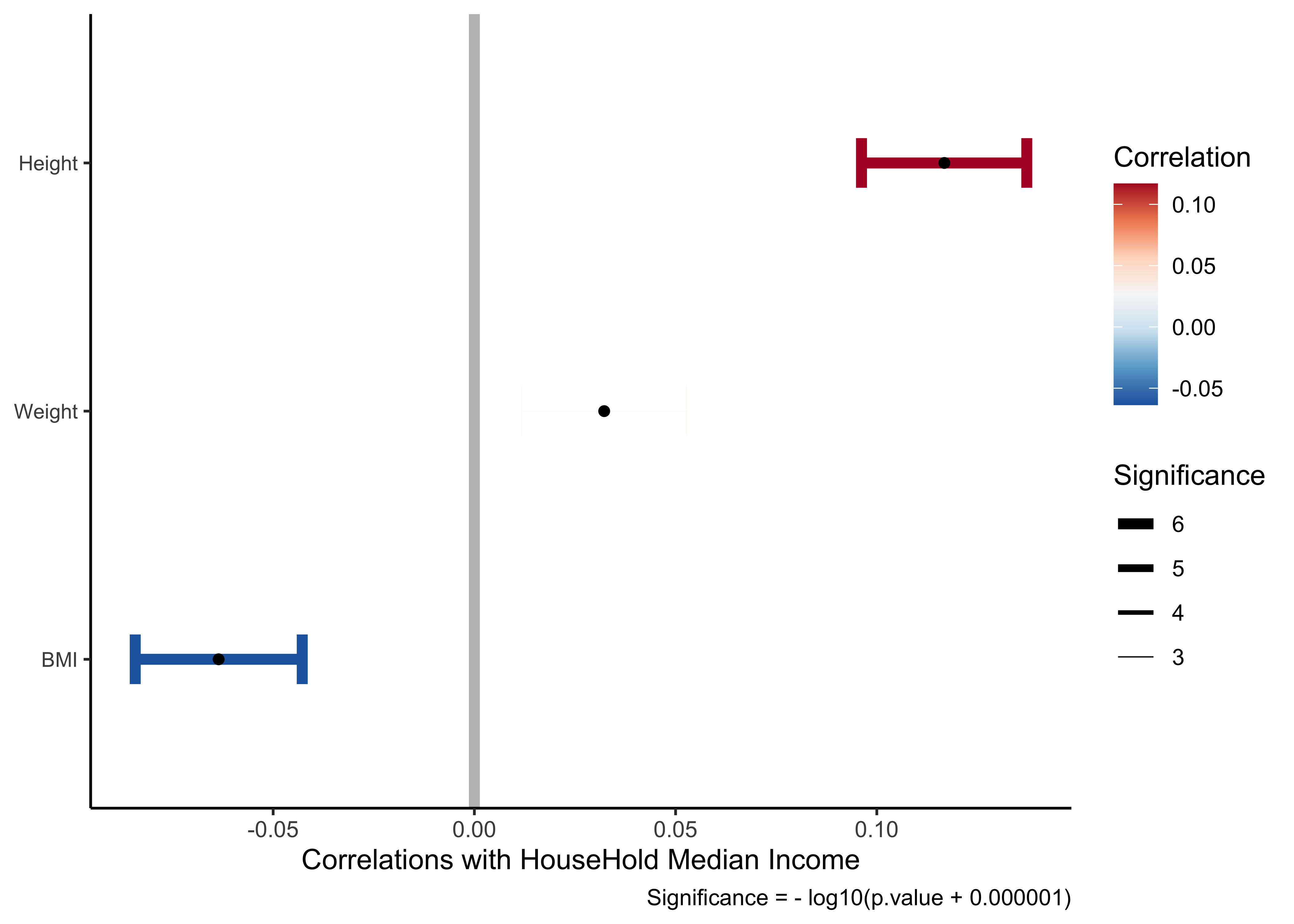
HHIncome_corrs_select

ABCDEFGHIJ0123456789

predictor <chr>	estimate <dbl>	statistic <dbl>	p.value <dbl>	parameter <int>	conf.low <dbl>	conf.high <dbl>
Height	0.11678118	11.068061	2.745490e-28	8860	0.09619449	0.13726801
Weight	0.03225989	3.082044	2.061977e-03	9118	0.01174371	0.05274893
BMI	-0.06354938	-5.990481	2.173863e-09	8850	-0.08427016	-0.04277366

HHIncome_corrs_select %>% 
  
  # arrange the predictors in order of their correlation scores
  # with the target variable (`height`)
  # Add errorbars to show uncertainty ranges / confidence intervals
  # Use errorbar width and linewidth fo emphasis
  gf_errorbar(conf.high + conf.low ~ reorder(predictor, estimate),
              color = ~ estimate,
              width = 0.2,
              linewidth = ~ -log10(p.value + 0.000001)) %>% 
  
  # All correlation estimates as points
  gf_point(estimate ~ reorder(predictor, estimate), 
           color = "black") %>% 
  
  # Reference line at zero correlation score
  gf_hline(yintercept = 0, color = "grey", linewidth = 2) %>% 
  
  # Themes,Titles, and Scales
  gf_labs(x = NULL, y = "Correlations with HouseHold Median Income", 
          caption = "Significance = - log10(p.value + 0.000001)") %>% 
  
  gf_theme(theme_classic()) %>%

  
  # Scale for colour
  gf_refine(guides(linewidth = guide_legend(reverse = TRUE)),
            scale_colour_distiller("Correlation", type = "div", 
                                    palette = "RdBu"),
            
  # Scale for dumbbells!!
  scale_linewidth_continuous("Significance", range = c(0.05,2)),
  
  theme(axis.text.y = element_text(size = 8, hjust = 1)),
  coord_flip())

So we might say taller people make more money? And fatter people make slightly less money? Well, the magnitude of the correlations (aka effect size) are low so we would not imagine this to be a hypothesis that we can defend.

Let us look at the Testosterone variable: trying all variables shows some paucity of observations ( due to missing data), so we will stick with our chosen variables:

Testosterone_corrs <- NHANES %>%
  select(Height, Weight, BMI) %>%
  
  # leave off height to get all the remaining ones
  #select(- Testosterone) %>%
  
  # perform a cor.test for all variables against height
  purrr::map(.x = .,
             .f = \(x) cor.test(x, NHANES$Testosterone)) %>%
  
  # tidy up the cor.test outputs into a tidy data frame
  map_dfr(broom::tidy, .id = "predictor")

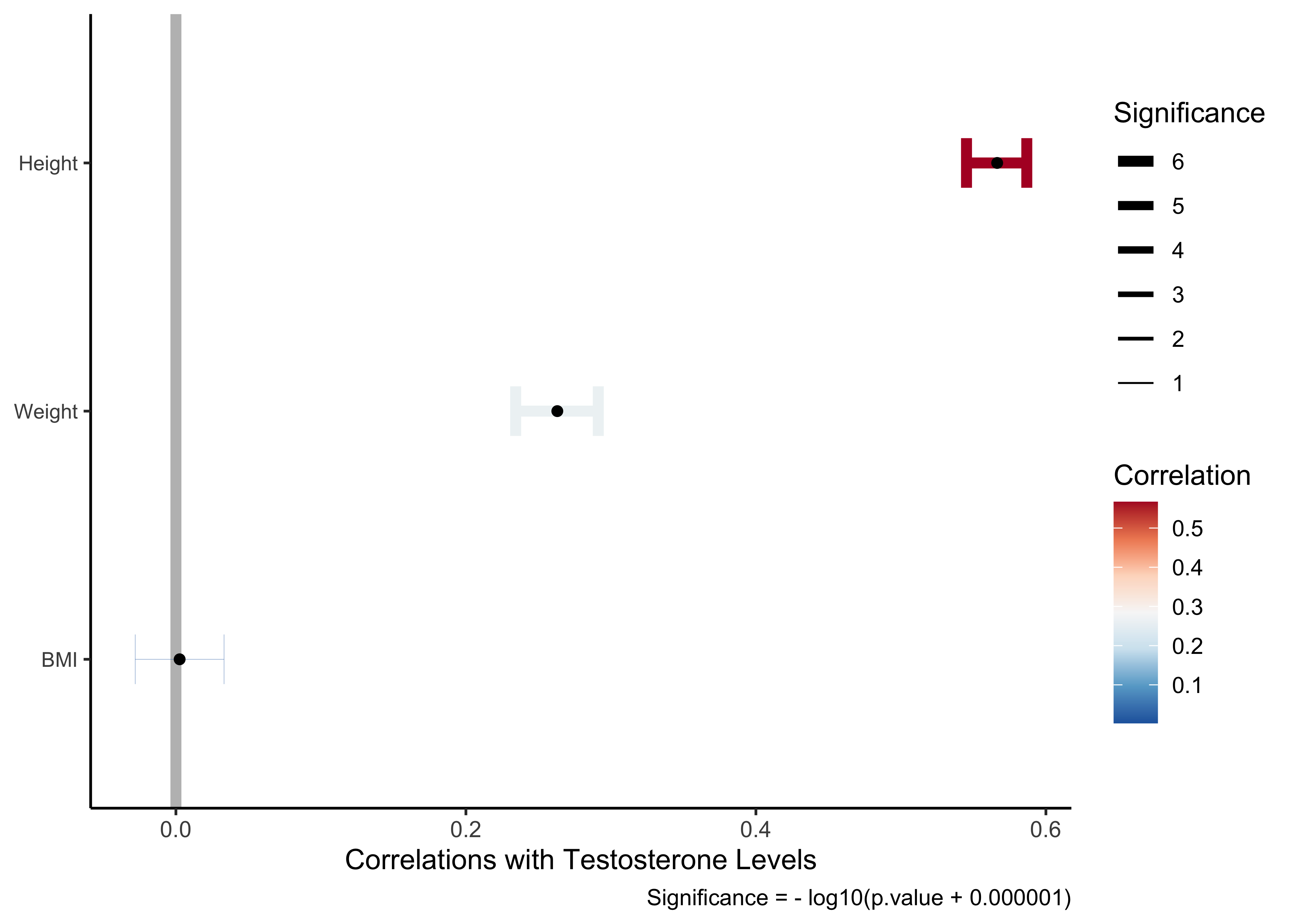
Testosterone_corrs

ABCDEFGHIJ0123456789

predictor <chr>	estimate <dbl>	statistic <dbl>	p.value <dbl>	parameter <int>	conf.low <dbl>	conf.high <dbl>
Height	0.566387816	44.0160781	0.000000e+00	4102	0.54524025	0.5868149
Weight	0.263033283	17.4528094	7.478487e-66	4098	0.23430874	0.2912990
BMI	0.002570577	0.1644974	8.693477e-01	4095	-0.02805397	0.0331903

Testosterone_corrs %>%
  
  # Reference line at zero correlation score
  gf_hline(yintercept = 0,
           color = "grey",
           linewidth = 2) %>%
  
  # arrange the predictors in order of their correlation scores
  # with the target variable (`height`)
  # Add errorbars to show uncertainty ranges / confidence intervals
  # Use errorbar width and linewidth fo emphasis
  gf_errorbar(
    conf.high + conf.low ~ reorder(predictor, estimate),
    color = ~ estimate,
    width = 0.2,
    linewidth = ~ -log10(p.value + 0.000001)
  ) %>%
  
  # All correlation estimates as points
  gf_point(estimate ~ reorder(predictor, estimate),
           color = "black") %>%
  
  
  # Themes,Titles, and Scales
  gf_labs(x = NULL, y = "Correlations with Testosterone Levels",
          caption = "Significance = - log10(p.value + 0.000001)") %>%
  
  gf_theme(theme_classic()) %>%
  
  
  # Scale for colour
  gf_refine(
    guides(linewidth = guide_legend(reverse = TRUE)),
    scale_colour_distiller("Correlation", type = "div",
                           palette = "RdBu"),
    
    # Scale for dumbbells!!
    scale_linewidth_continuous("Significance", range = c(0.05, 2)),
    
    theme(axis.text.y = element_text(size = 8, hjust = 1)),
    coord_flip()
  )

Conclusion

We have a decent Correlations related workflow in R:

Load the dataset
inspect/skim/glimpse the dataset, identify Quant and Qual variables
Identify a target variable based on your knowledge of the data, how it was gathered, who gathered it and what was their intent
Develop Pair-Wise plots + Correlations using GGally::ggpairs()
Develop Correlogram corrplot::corrplot
Check everything with a cor_test: effect size,significance, confidence intervals
Use purrr + cor.test to plot correlations and confidence intervals for multiple Quant predictor variables against the target variable
Plot scatter plots using gf_point.
Add extra lines using gf_abline() to compare hypotheses that you may have.

References

R Package Citations

Package	Version	Citation
corrplot	0.92	Wei and Simko (2021)
GGally	2.2.1	Schloerke et al. (2024)
ggformula	0.12.0	Kaplan and Pruim (2023)
mosaic	1.9.1	Pruim, Kaplan, and Horton (2017)
mosaicData	0.20.4	Pruim, Kaplan, and Horton (2023)
NHANES	2.1.0	Pruim (2015)
TeachHist	0.2.1	Lange (2023)
TeachingDemos	2.13	Snow (2024)

Kaplan, Daniel, and Randall Pruim. 2023. ggformula: Formula Interface to the Grammar of Graphics. https://CRAN.R-project.org/package=ggformula.

Lange, Carsten. 2023. TeachHist: A Collection of Amended Histograms Designed for Teaching Statistics. https://CRAN.R-project.org/package=TeachHist.

Pruim, Randall. 2015. NHANES: Data from the US National Health and Nutrition Examination Study. https://CRAN.R-project.org/package=NHANES.

Pruim, Randall, Daniel T Kaplan, and Nicholas J Horton. 2017. “The Mosaic Package: Helping Students to ‘Think with Data’ Using r.” The R Journal 9 (1): 77–102. https://journal.r-project.org/archive/2017/RJ-2017-024/index.html.

Pruim, Randall, Daniel Kaplan, and Nicholas Horton. 2023. mosaicData: Project MOSAIC Data Sets. https://CRAN.R-project.org/package=mosaicData.

Schloerke, Barret, Di Cook, Joseph Larmarange, Francois Briatte, Moritz Marbach, Edwin Thoen, Amos Elberg, and Jason Crowley. 2024. GGally: Extension to “ggplot2”. https://CRAN.R-project.org/package=GGally.

Snow, Greg. 2024. TeachingDemos: Demonstrations for Teaching and Learning. https://CRAN.R-project.org/package=TeachingDemos.

Wei, Taiyun, and Viliam Simko. 2021. R Package “corrplot”: Visualization of a Correlation Matrix. https://github.com/taiyun/corrplot.

Footnotes

http://euclid.psych.yorku.ca/SCS/Gallery/images/galton-corr.jpg>↩︎
https://www.researchgate.net/figure/Galtons-smoothed-correlation-diagram-for-the-data-on-heights-of-parents-and-children_fig15_226400313↩︎

Citation

BibTeX citation:

@online{venkatadri2022,
  author = {Venkatadri, Arvind},
  title = {Tutorial on {Correlations} in {R}},
  date = {2022-11-22},
  url = {https://av-quarto.netlify.app/content/courses/Analytics/Descriptive/Modules/30-Correlations/files/correlations.html},
  langid = {en},
  abstract = {Tests, Tables, and Graphs for Correlations in R}
}

For attribution, please cite this work as:

Venkatadri, Arvind. 2022. “Tutorial on Correlations in R.” November 22, 2022. https://av-quarto.netlify.app/content/courses/Analytics/Descriptive/Modules/30-Correlations/files/correlations.html.

Introduction

Setting up R Packages

Case Study 1: Galton Dataset from mosaicData

Inspecting the Data

Correlations and Plots

Visualizing Uncertainty in Correlation Estimates

Case Study#2: Dataset from NHANES

Inspecting the Data

Correlations and Plots

Visualizing Uncertainty in Correlation Estimates

Conclusion

References

R Package Citations

Footnotes

Citation

Case Study 1: Galton Dataset from `mosaicData`

Case Study#2: Dataset from `NHANES`