Change

Correlations

Scatter Plots

Bubble Plots

Errorbar Plot

Heatmaps

Regression Lines

Author

Arvind V.

Published

November 22, 2022

Modified

July 29, 2025

Abstract

How one variable changes with another

WebR Status

🟡 Loading...

Slides and Tutorials

Tutorial

R (Interactive Graphs

“The world says: ‘You have needs – satisfy them. You have as much right as the rich and the mighty. Don’t hesitate to satisfy your needs; indeed, expand your needs and demand more.’ This is the worldly doctrine of today. And they believe that this is freedom. The result for the rich is isolation and suicide, for the poor, envy and murder.”

— Fyodor Dostoevsky

Setting up R Packages

library(GGally) # Corr plots
library(corrplot) # More corrplots
library(ggExtra) # Making Combination Plots

# library(devetools)
# devtools::install_github("rpruim/Lock5withR")
library(Lock5withR) # Datasets
library(palmerpenguins) # A famous dataset

library(easystats) # Easy Statistical Analysis and Charts
library(correlation) # Different Types of Correlations
# From the easystats collection of packages
##
library(tidyplots) # Easily Produced Publication-Ready Plots
library(tinyplot) # Plots with Base R
library(tinytable) # Elegant Tables for our data


library(ggformula) # Formula based plots
library(mosaic) # Our go-to package
library(skimr) # Another Data inspection package
library(tidyverse) # Tidy data processing and plotting

Plot Fonts and Theme

Show the Code

library(systemfonts)
library(showtext)
## Clean the slate
systemfonts::clear_local_fonts()
systemfonts::clear_registry()
##
showtext_opts(dpi = 96) # set DPI for showtext
sysfonts::font_add(
  family = "Alegreya",
  regular = "../../../../../../fonts/Alegreya-Regular.ttf",
  bold = "../../../../../../fonts/Alegreya-Bold.ttf",
  italic = "../../../../../../fonts/Alegreya-Italic.ttf",
  bolditalic = "../../../../../../fonts/Alegreya-BoldItalic.ttf"
)

sysfonts::font_add(
  family = "Roboto Condensed",
  regular = "../../../../../../fonts/RobotoCondensed-Regular.ttf",
  bold = "../../../../../../fonts/RobotoCondensed-Bold.ttf",
  italic = "../../../../../../fonts/RobotoCondensed-Italic.ttf",
  bolditalic = "../../../../../../fonts/RobotoCondensed-BoldItalic.ttf"
)
showtext_auto(enable = TRUE) # enable showtext
##
theme_custom <- function() {
  font <- "Alegreya" # assign font family up front

  theme_classic(base_size = 14, base_family = font) %+replace% # replace elements we want to change

    theme(
      text = element_text(family = font), # set base font family

      # text elements
      plot.title = element_text( # title
        family = font, # set font family
        size = 24, # set font size
        face = "bold", # bold typeface
        hjust = 0, # left align
        margin = margin(t = 5, r = 0, b = 5, l = 0)
      ), # margin
      plot.title.position = "plot",
      plot.subtitle = element_text( # subtitle
        family = font, # font family
        size = 14, # font size
        hjust = 0, # left align
        margin = margin(t = 5, r = 0, b = 10, l = 0)
      ), # margin

      plot.caption = element_text( # caption
        family = font, # font family
        size = 9, # font size
        hjust = 1
      ), # right align

      plot.caption.position = "plot", # right align

      axis.title = element_text( # axis titles
        family = "Roboto Condensed", # font family
        size = 12
      ), # font size

      axis.text = element_text( # axis text
        family = "Roboto Condensed", # font family
        size = 9
      ), # font size

      axis.text.x = element_text( # margin for axis text
        margin = margin(5, b = 10)
      )

      # since the legend often requires manual tweaking
      # based on plot content, don't define it here
    )
}

Show the Code

```{r}
#| cache: false
#| code-fold: true
## Set the theme
theme_set(new = theme_custom())
```

Error in theme_set(new = theme_custom()): could not find function "theme_set"

Show the Code

```{r}
#| cache: false
#| code-fold: true
## Use available fonts in ggplot text geoms too!
update_geom_defaults(geom = "text", new = list(
  family = "Roboto Condensed",
  face = "plain",
  size = 3.5,
  color = "#2b2b2b"
))
```

Error in update_geom_defaults(geom = "text", new = list(family = "Roboto Condensed", : could not find function "update_geom_defaults"

What graphs will we see today?

Variable #1	Variable #2	Chart Names	Chart Shape
Quant	Quant	Scatter Plot

Some of the very basic and commonly used plots for data are:

Scatter Plot for two variables
~~Contour Plot~~
~~Scatter Plot with Confidence Ellipses~~
Pairwise Correlation Plots for multiple variables
Correlogram for multiple variables
Heatmap for multiple variables
Errorbar chart for multiple variables
Combination chart with marginal densities

What kind of Data Variables will we choose?

No	Pronoun	Answer	Variable/Scale	Example	What Operations?
1	How Many / Much / Heavy? Few? Seldom? Often? When?	Quantities, with Scale and a Zero Value.Differences and Ratios /Products are meaningful.	Quantitative/Ratio	Length,Height,Temperature in Kelvin,Activity,Dose Amount,Reaction Rate,Flow Rate,Concentration,Pulse,Survival Rate	Correlation

Inspiration

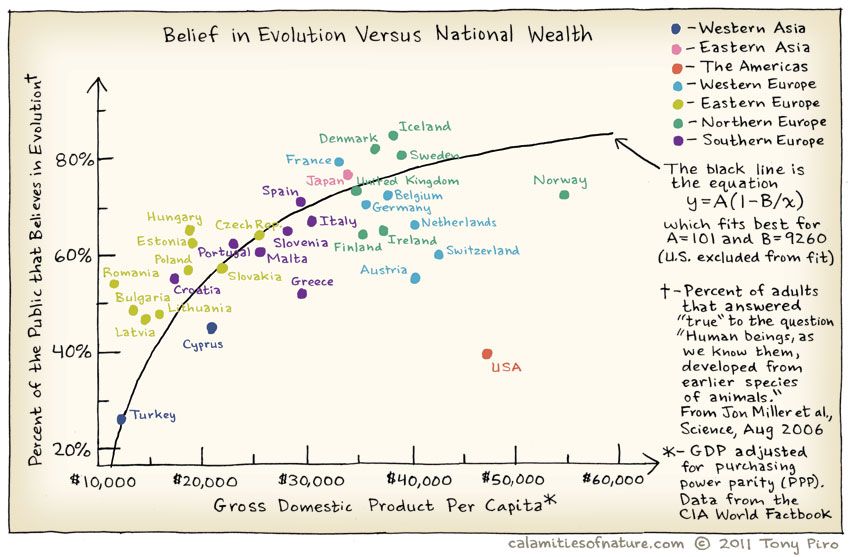
Does belief in Evolution depend upon the GSP of of the country? Where is the US in all of this? Does the Bible Belt tip the scales here?

And India?

What is Correlation?

One of the basic Questions we would have of our data is: Does some variable depend upon another in some way? Does $y$ vary with $x$ ? A Correlation Test is designed to answer exactly this question.

The word correlation is used in everyday life to denote some form of association. We might say that we have noticed a correlation between rainy days and reduced sales at supermarkets. However, in statistical terms we use correlation to denote association between two quantitative variables. We also assume that the association is linear, that one variable increases or decreases a fixed amount for a unit increase or decrease in the other. The other technique that is often used in these circumstances is regression, which involves estimating the best straight line to summarise the association.

Pearson Correlation coefficient

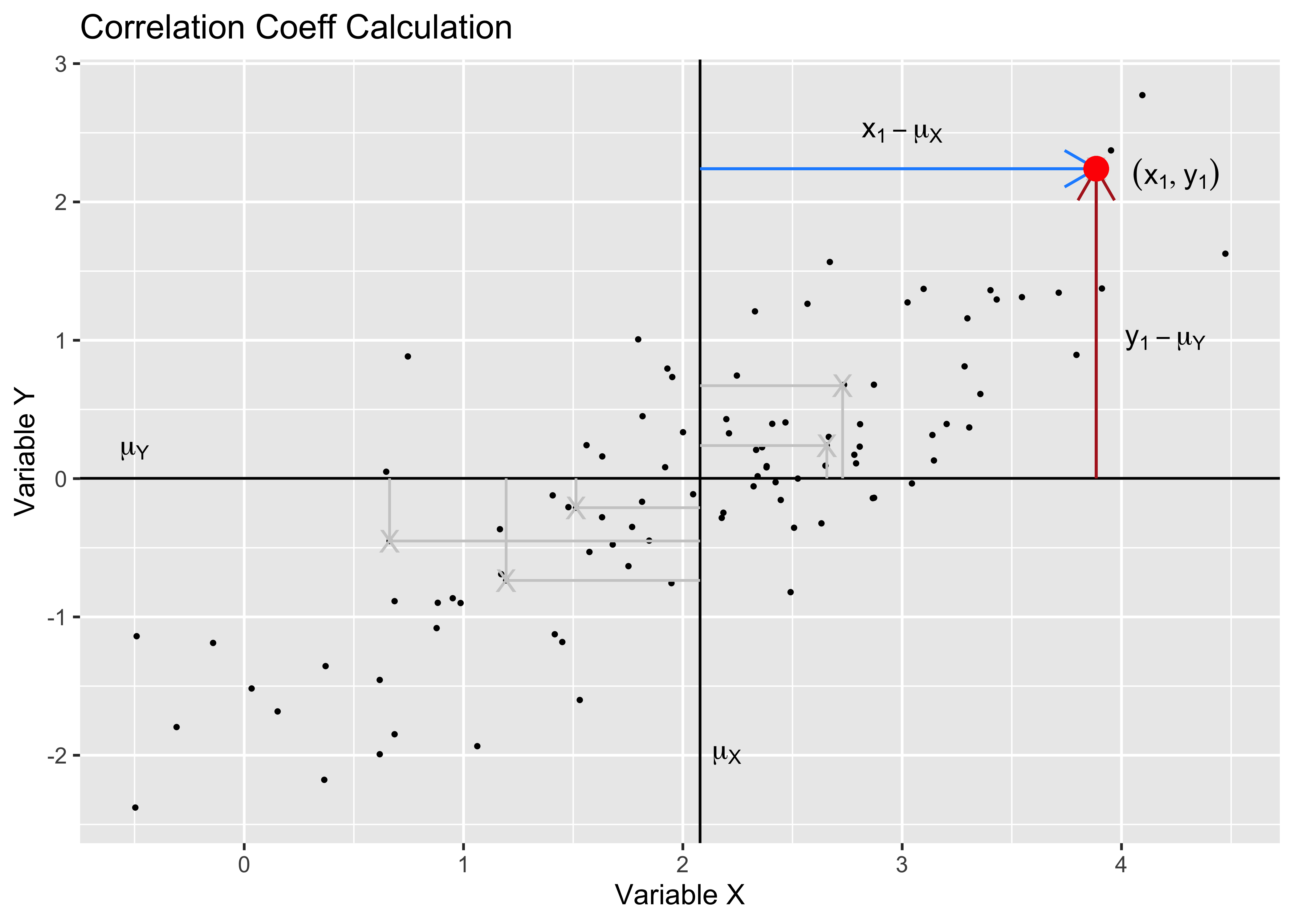
The degree of association is measured by a correlation coefficient, denoted by r. It is sometimes called Pearson’s correlation coefficient after its originator and is a measure of linear association. (If a curved line is needed to express the relationship, other and more complicated measures of the correlation must be used.)

The correlation coefficient is measured on a scale that varies from + 1 through 0 to – 1. Complete correlation between two variables is expressed by either + 1 or -1. When one variable increases as the other increases the correlation is positive; when one decreases as the other increases it is negative.

In formal terms, the correlation between two variables $x$ and $y$ is defined as

$ρ = E [\frac{(x - μ_{x}) * (y - μ_{y})}{(σ_{x}) * (σ_{y})}]$

where $E$ is the expectation operator ( i.e taking mean ). Think of this as the average of the products of two scaled variables.

Pearson Correlation uses z-scores

We can see $(x - μ_{x}) / σ_{x}$ is a centering and scaling of the variable $x$ . Recall from our discussion on Distributions that this is called the z-score of x.

Pearson correlation assumes that the relationship between the two variables is linear. There are of course many other types of correlation measures: some which work when this is not so. Type vignette("types", package = "correlation") in your Console to see the vignette from the correlation package that discusses various types of correlation measures.

Case Study-1: `HollywoodMovies2011` dataset

Let us look at the HollywoodMovies2011 dataset from the Lock5withR package. The dataset is also available by clicking the icon below ( in case you are not able to install Lock5withR):

Inspecting the Data

HollywoodMovies2011 -> movies
glimpse(movies)

Rows: 136
Columns: 14
$ Movie             <fct> "Insidious", "Paranormal Activity 3", "Bad Teacher",…
$ LeadStudio        <fct> Sony, Independent, Independent, Warner Bros, Relativ…
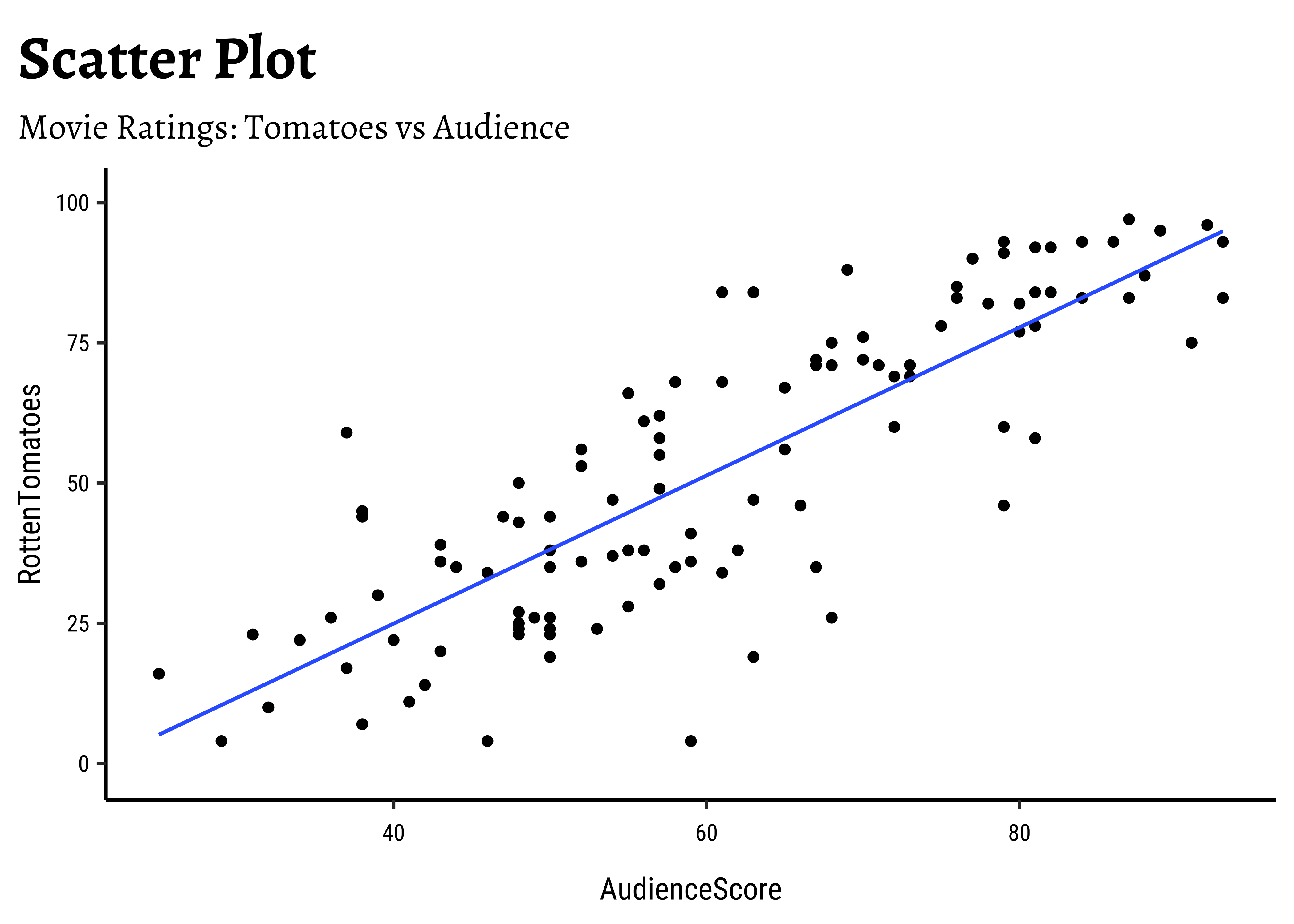
$ RottenTomatoes    <int> 67, 68, 44, 96, 90, 93, 75, 35, 63, 69, 69, 49, 26, …
$ AudienceScore     <int> 65, 58, 38, 92, 77, 84, 91, 58, 74, 73, 72, 57, 68, …
$ Story             <fct> Monster Force, Monster Force, Comedy, Rivalry, Rival…
$ Genre             <fct> Horror, Horror, Comedy, Fantasy, Comedy, Romance, Dr…
$ TheatersOpenWeek  <int> 2408, 3321, 3049, 4375, 2918, 944, 2534, 3615, NA, 2…
$ BOAverageOpenWeek <int> 5511, 15829, 10365, 38672, 8995, 6177, 10278, 23775,…
$ DomesticGross     <dbl> 54.01, 103.66, 100.29, 381.01, 169.11, 56.18, 169.22…
$ ForeignGross      <dbl> 43.00, 98.24, 115.90, 947.10, 119.28, 83.00, 30.10, …
$ WorldGross        <dbl> 97.009, 201.897, 216.196, 1328.111, 288.382, 139.177…
$ Budget            <dbl> 1.5, 5.0, 20.0, 125.0, 32.5, 17.0, 25.0, 80.0, 0.2, …
$ Profitability     <dbl> 64.672667, 40.379400, 10.809800, 10.624888, 8.873292…
$ OpeningWeekend    <dbl> 13.27, 52.57, 31.60, 169.19, 26.25, 5.83, 26.04, 85.…

Business Insights from Data Inspection

movies has 136 observations on the following 14 variables.

Movie a factor with many levels
LeadStudio a factor with many levels
RottenTomatoes a numeric vector
AudienceScore a numeric vector
Story a factor with many levels
Genre a factor with levels Action, Adventure, Animation, Comedy, Drama, Fantasy, Horror, Romance, Thriller.
TheatersOpenWeek a numeric vector. No. of theatres.
BOAverageOpenWeek a numeric vector.
DomesticGross a numeric vector. In million USD.
ForeignGross a numeric vector. In million USD.
WorldGross a numeric vector. In million USD.
Budget a numeric vector. In million USD.
Profitability a numeric vector. A ratio
OpeningWeekend a numeric vector. In million USD.

There are no missing values in the Qual variables; but some entries in the Quant variables are missing. skim throws a warning that we may need to examine later.

Let us look at the Quant variables: are these related in anyway? Could the relationship between any two Quant variables also depend upon the level of a Qual variable?

Scatter Plots

Which are the numeric variables in movies?

R
web-r

movies_quant <- movies %>%
  drop_na() %>%
  select(where(is.numeric))
movies_quant

ABCDEFGHIJ0123456789

RottenTomatoes <int>	AudienceScore <int>	TheatersOpenWeek <int>	BOAverageOpenWeek <int>	DomesticGross <dbl>	ForeignGross <dbl>	WorldGross <dbl>	Budget <dbl>	Profitability <dbl>	OpeningWeekend <dbl>
67	65	2408	5511	54.01	43.00	97.009	1.5	64.6726667	13.27
68	58	3321	15829	103.66	98.24	201.897	5.0	40.3794000	52.57
44	38	3049	10365	100.29	115.90	216.196	20.0	10.8098000	31.60
96	92	4375	38672	381.01	947.10	1328.111	125.0	10.6248880	169.19
90	77	2918	8995	169.11	119.28	288.382	32.5	8.8732923	26.25
93	84	944	6177	56.18	83.00	139.177	17.0	8.1868824	5.83
75	91	2534	10278	169.22	30.10	199.324	25.0	7.9729600	26.04
35	58	3615	23775	254.46	327.00	581.464	80.0	7.2683000	85.95
69	73	2756	6860	79.25	82.60	161.849	27.0	5.9944074	18.91
69	72	3040	9310	117.54	92.10	209.638	35.0	5.9896571	28.30

Now let us plot their relationships.

movies %>%
  drop_na() %>%
  gf_point(DomesticGross ~ WorldGross) %>%
  gf_lm() %>%
  gf_labs(
    title = "Scatter Plot",
    subtitle = "Movie Gross Earnings: Domestics vs World"
  )

movies %>%
  drop_na() %>%
  gf_point(Profitability ~ OpeningWeekend) %>%
  gf_lm() %>%
  gf_labs(
    title = "Scatter Plot",
    subtitle = "Movies: Does Opening Week Earnings indicate Profitability?"
  )

movies %>%
  drop_na() %>%
  gf_point(RottenTomatoes ~ AudienceScore) %>%
  gf_lm() %>%
  gf_labs(
    title = "Scatter Plot",
    subtitle = "Movie Ratings: Tomatoes vs Audience"
  )

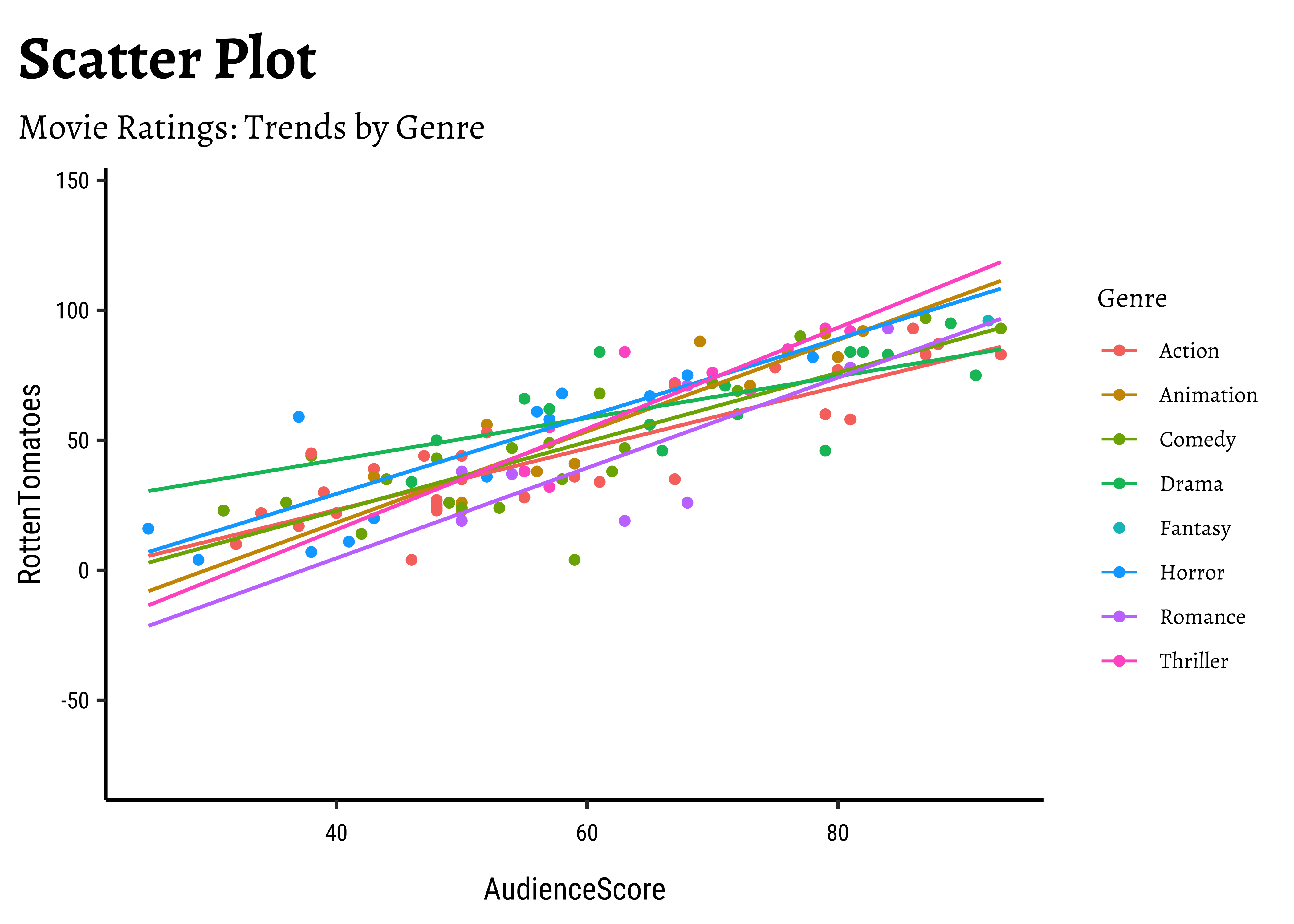
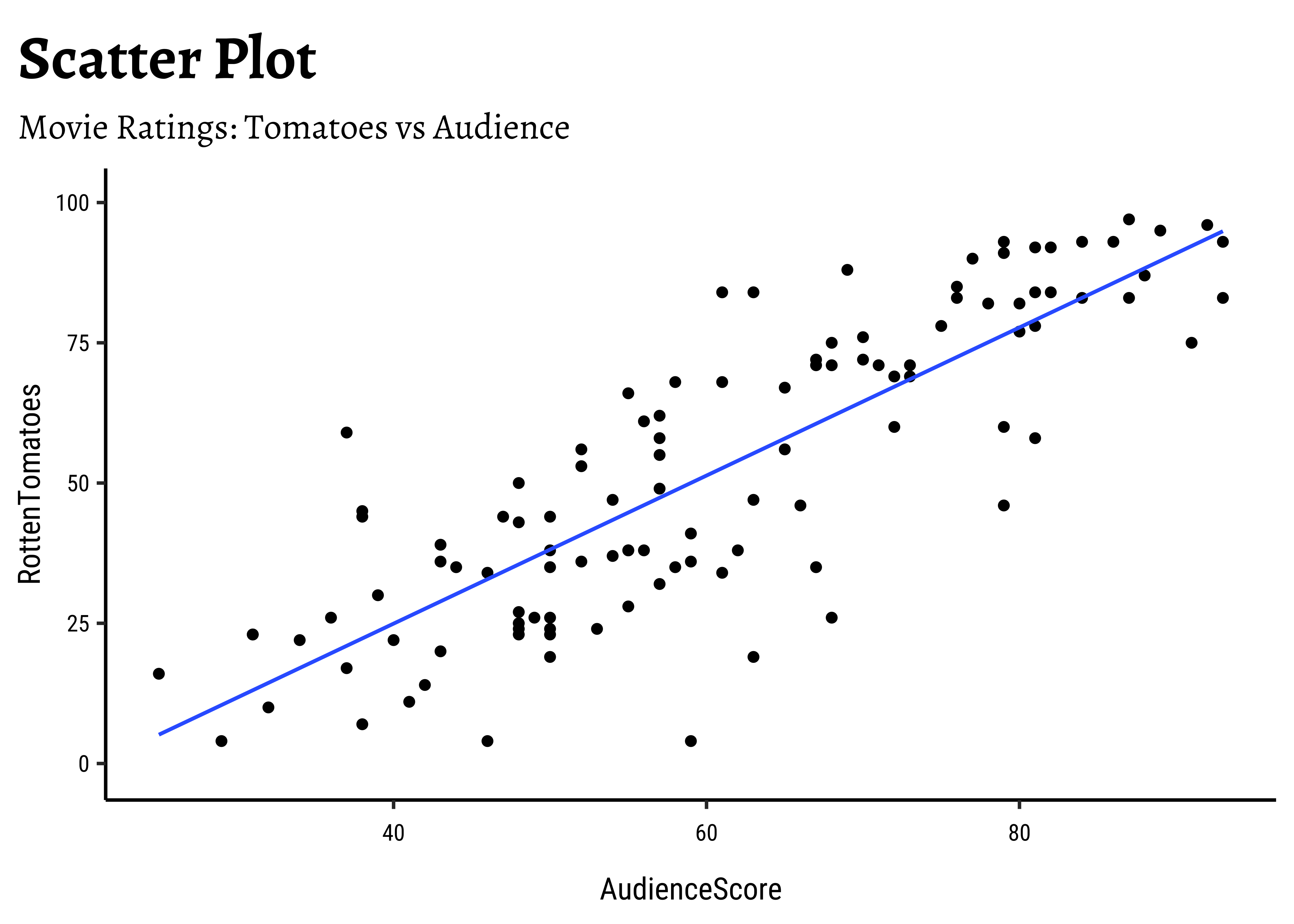
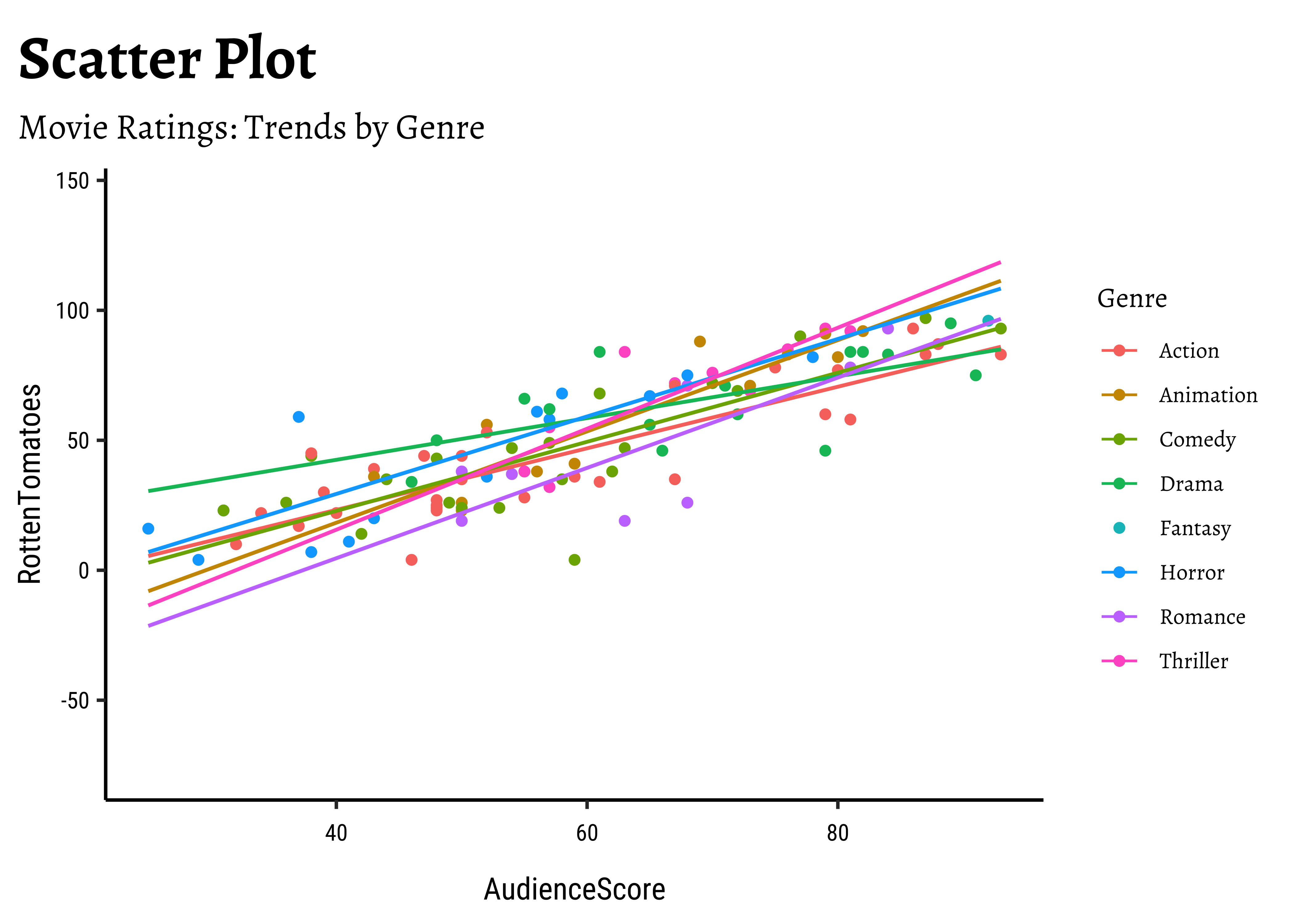
We can split some of the scatter plots using one or other of the Qual variables. For instance, is the relationship between the two ratings the same, regardless of movie genre?

movies %>%
  drop_na() %>%
  gf_point(RottenTomatoes ~ AudienceScore,
    color = ~Genre
  ) %>%
  gf_lm() %>%
  gf_labs(
    title = "Scatter Plot",
    subtitle = "Movie Ratings: Trends by Genre"
  )

movies %>%
  drop_na() %>%
  ggplot(aes(x = DomesticGross, y = WorldGross)) +
  geom_point() +
  geom_lm() +
  labs(
    title = "Scatter Plot",
    subtitle = "Movie Gross Earnings: Domestics vs World"
  )

movies %>%
  drop_na() %>%
  ggplot(aes(OpeningWeekend, Profitability)) +
  geom_point() +
  geom_lm() +
  labs(
    title = "Scatter Plot",
    subtitle = "Movies: Does Opening Week Earnings indicate Profitability?"
  )

movies %>%
  drop_na() %>%
  ggplot(aes(AudienceScore, RottenTomatoes)) +
  geom_point() +
  geom_lm() +
  labs(
    title = "Scatter Plot",
    subtitle = "Movie Ratings: Tomatoes vs Audience"
  )

movies %>%
  drop_na() %>%
  ggplot(aes(RottenTomatoes, AudienceScore, color = Genre)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  labs(
    title = "Scatter Plot",
    subtitle = "Movie Ratings: Trends by Genre"
  )

## We can split some of the scatter plots using one or other of the Qual variables. For instance, is the relationship between the two ratings the same, regardless of movie genre?
movies %>%
  drop_na() %>%
  gf_point(RottenTomatoes ~ AudienceScore, 
           color = ~ Genre) %>%
  gf_lm() %>% 
  gf_labs(title = "Scatter Plot",
          subtitle = "Movie Ratings: Trends by Genre")

Business Insight from movies scatter plots

We have fitted a trend line to each of the scatter plots.

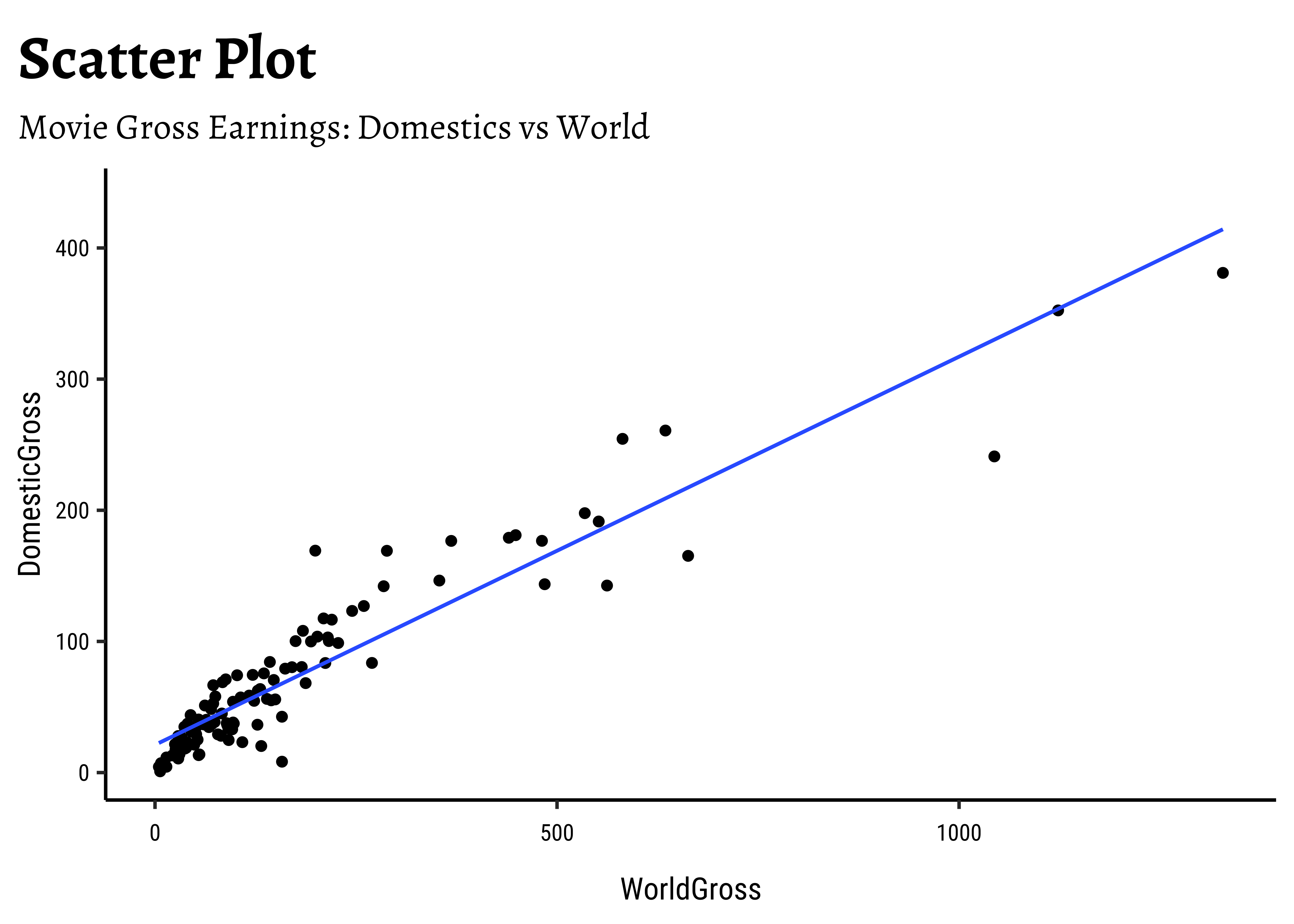
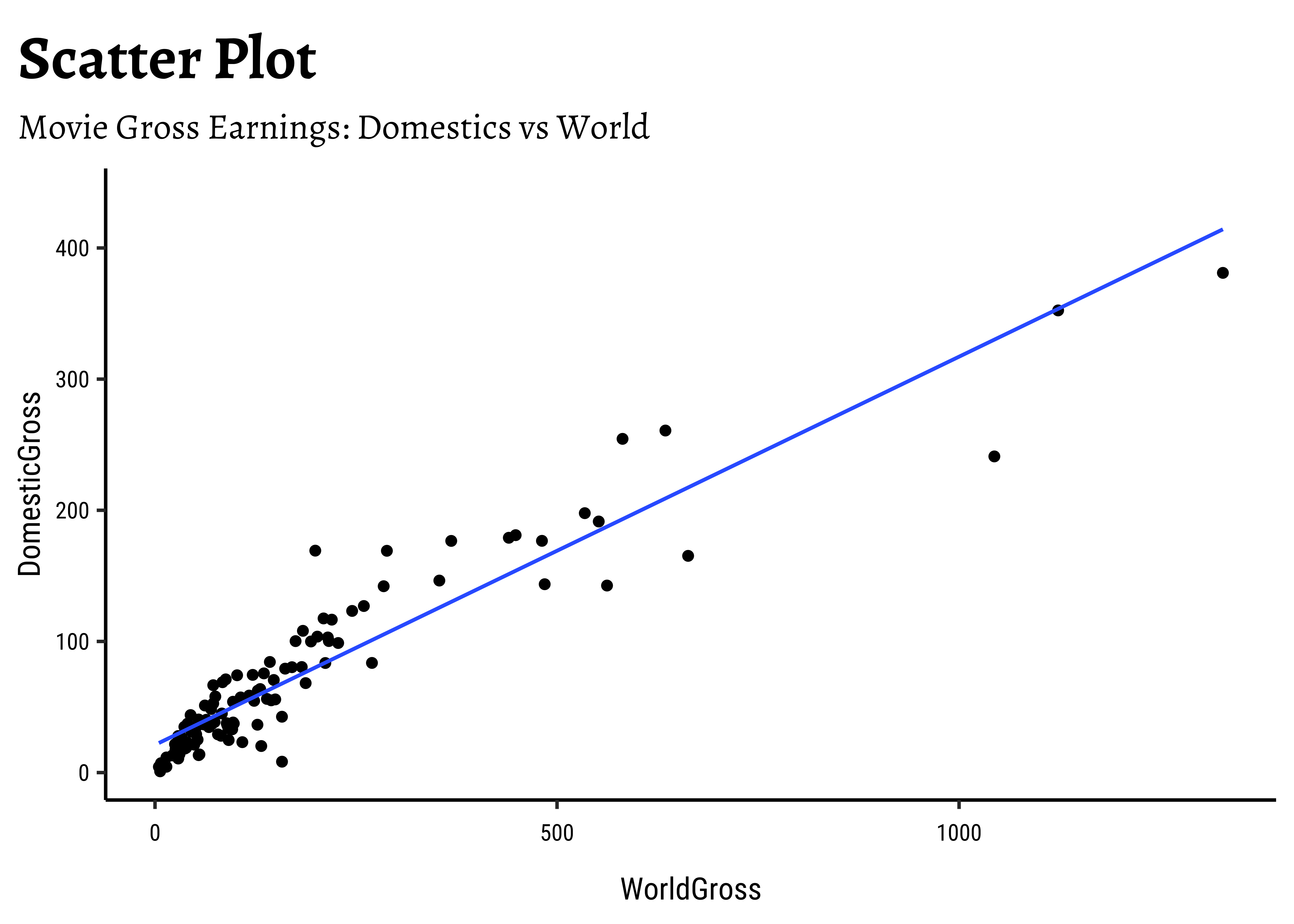
DomesticGross and World Gross are related, though there are fewer movies at the high end of DomesticGross…
AudienceScore and RottenTomatoes seem clearly related…both increase together.
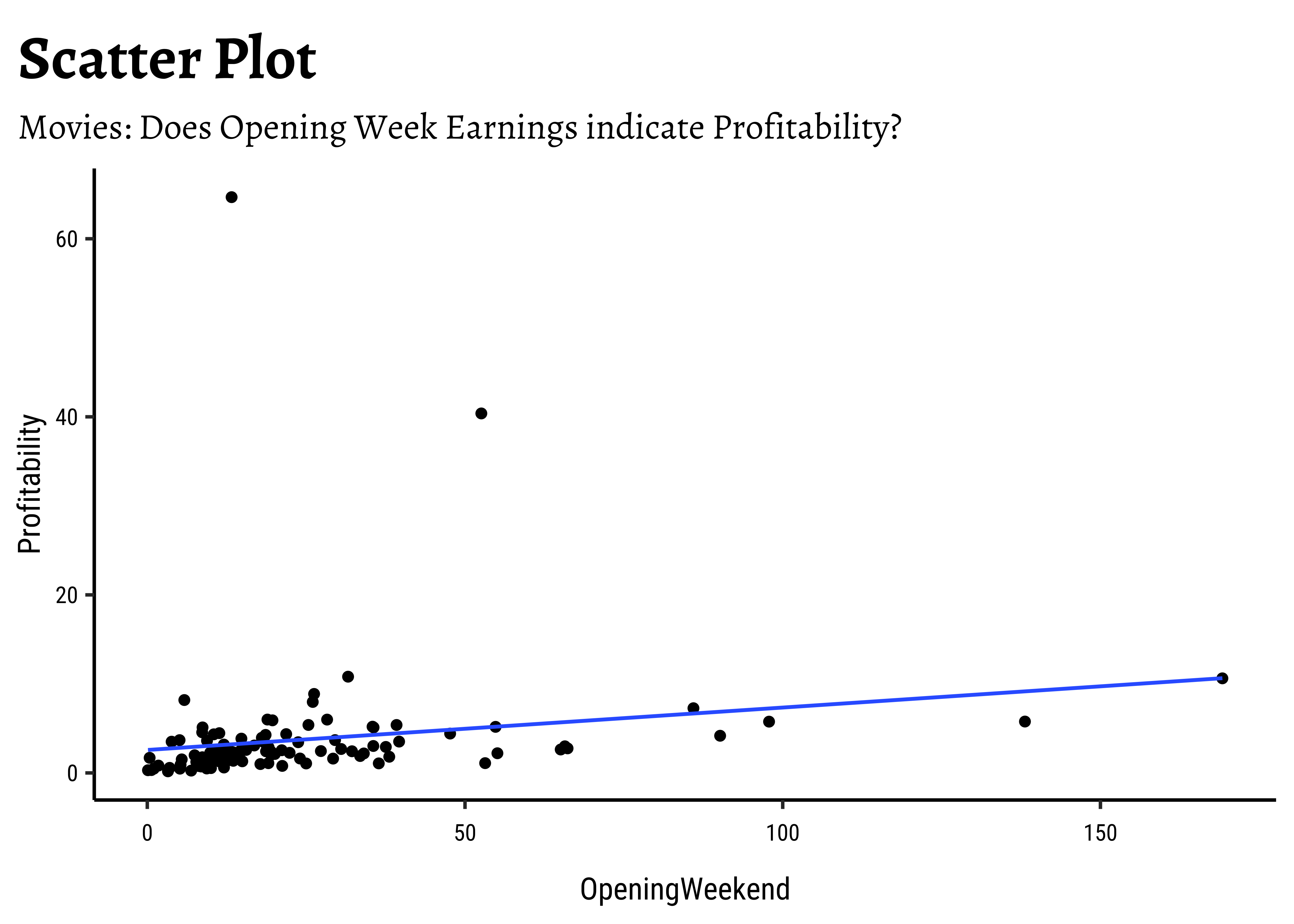
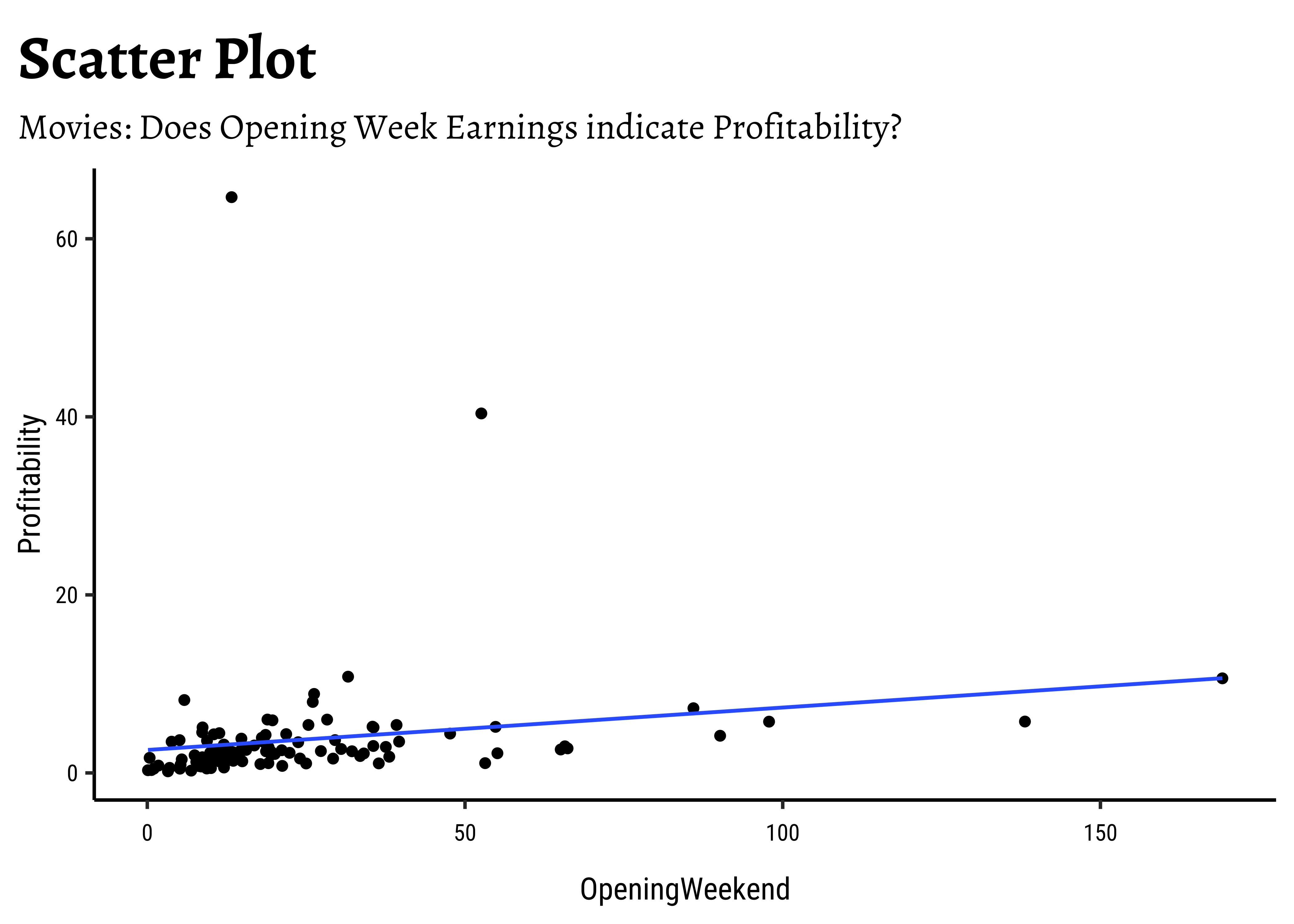
OpeningWeek and Profitability are also related in a linear way. There are just two movies which have been extremely profitable..but they do not influence the slope of the trend line too much, because of their location midway in the range of OpeningWeek. Influence is something that is a key concept in Linear Regression.
By and large, there are only small variations in slope across Genres.

Independent and Dependent Variables

Note that we have rather arbitrarily taken AudienceScore as the independent variable, to be plotted on the x-axis, and RottenTomatoes on the y-axis. It could easily have been the other way around, based on our Research Question. Datasets are gathered with specific Research Hypotheses in mind, so check the help file and also with the person who gathered the data about what variable they are interested in!

Quantizing Correlation

So we see that there are visible relationships between Quant variables. How do we quantize this relationship, into a correlation score?

There are two ways: using the GGally and corplot packages, and doing a formal correlation test with the mosaic package.

Using GGally
Using corrplot

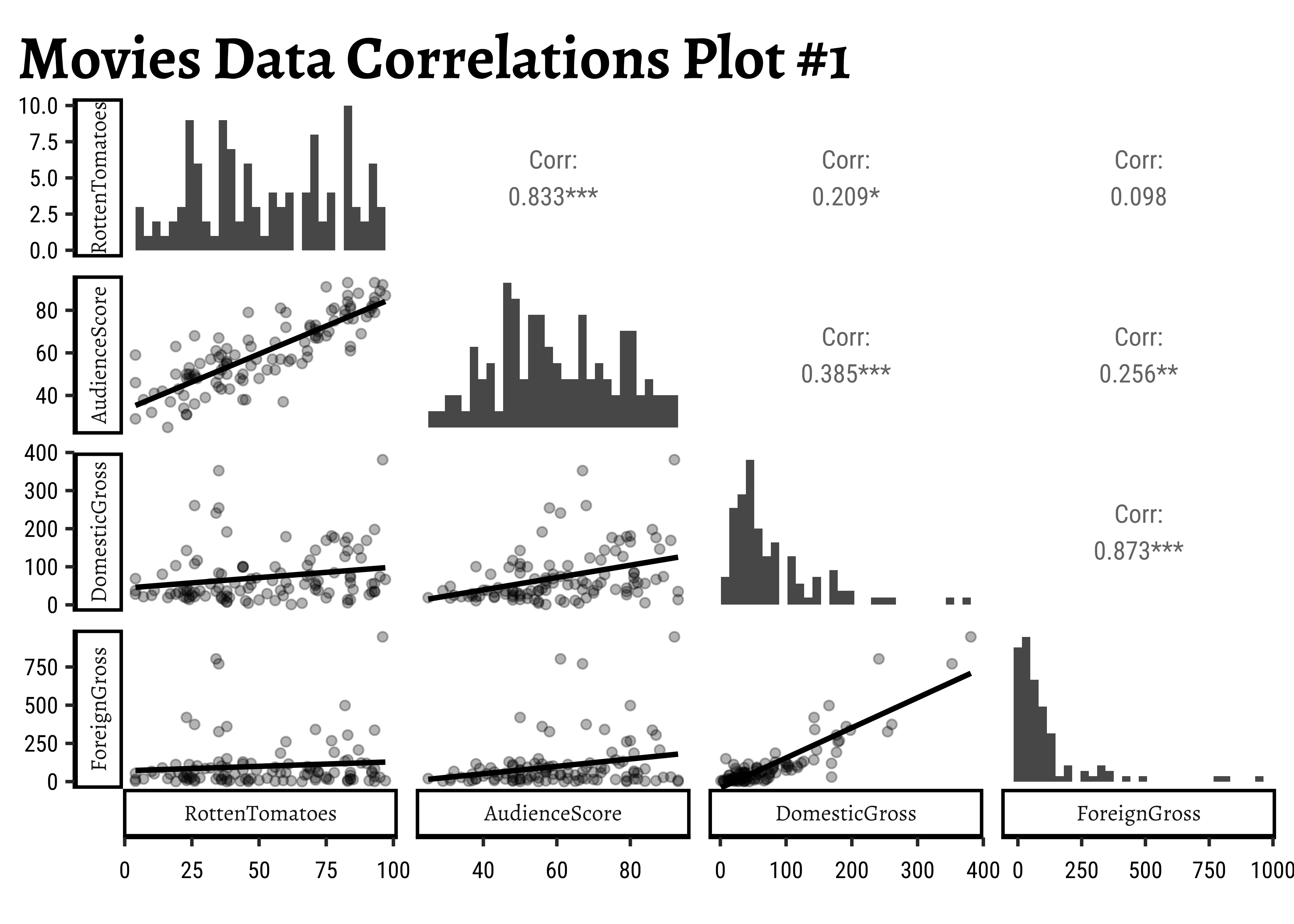
By default, GGally::ggpairs() provides:

two different comparisons of each pair of columns
displays either the density or count of the respective variable along the diagonal.
With different parameter settings, the diagonal can be replaced with the axis values and variable labels.

GGally::ggpairs(
  movies %>% drop_na(),
  # Select Quant variables only for now
  columns = c(
    "RottenTomatoes", "AudienceScore", "DomesticGross", "ForeignGross"
  ),
  switch = "both",
  # axis labels in more traditional locations(left and bottom)

  progress = FALSE,
  # no compute progress messages needed

  # Choose the diagonal graphs (always single variable! Think!)
  diag = list(continuous = "barDiag"),
  # choosing histogram,not density

  # Choose lower triangle graphs, two-variable graphs
  lower = list(continuous = wrap("smooth", alpha = 0.3, se = FALSE)),
  title = "Movies Data Correlations Plot #1"
)

Business Insight from Pairs Plot#1

As we saw earlier from the Scatter Plot, AudienceScore and RottenTomatoes are well correlated, with a correlation score of $0.833$
DomesticGross and ForeignGross are also extremely well correlated, with a score of $0.873$ .
Both these correlation scores are highly significant, with three stars. (We will speak of significance in a while.)
None of the other pairs of variables have good correlation scores.
Note in passing that both the “Gross” related variables have highly skewed distributions. That is the nature of the movie business!

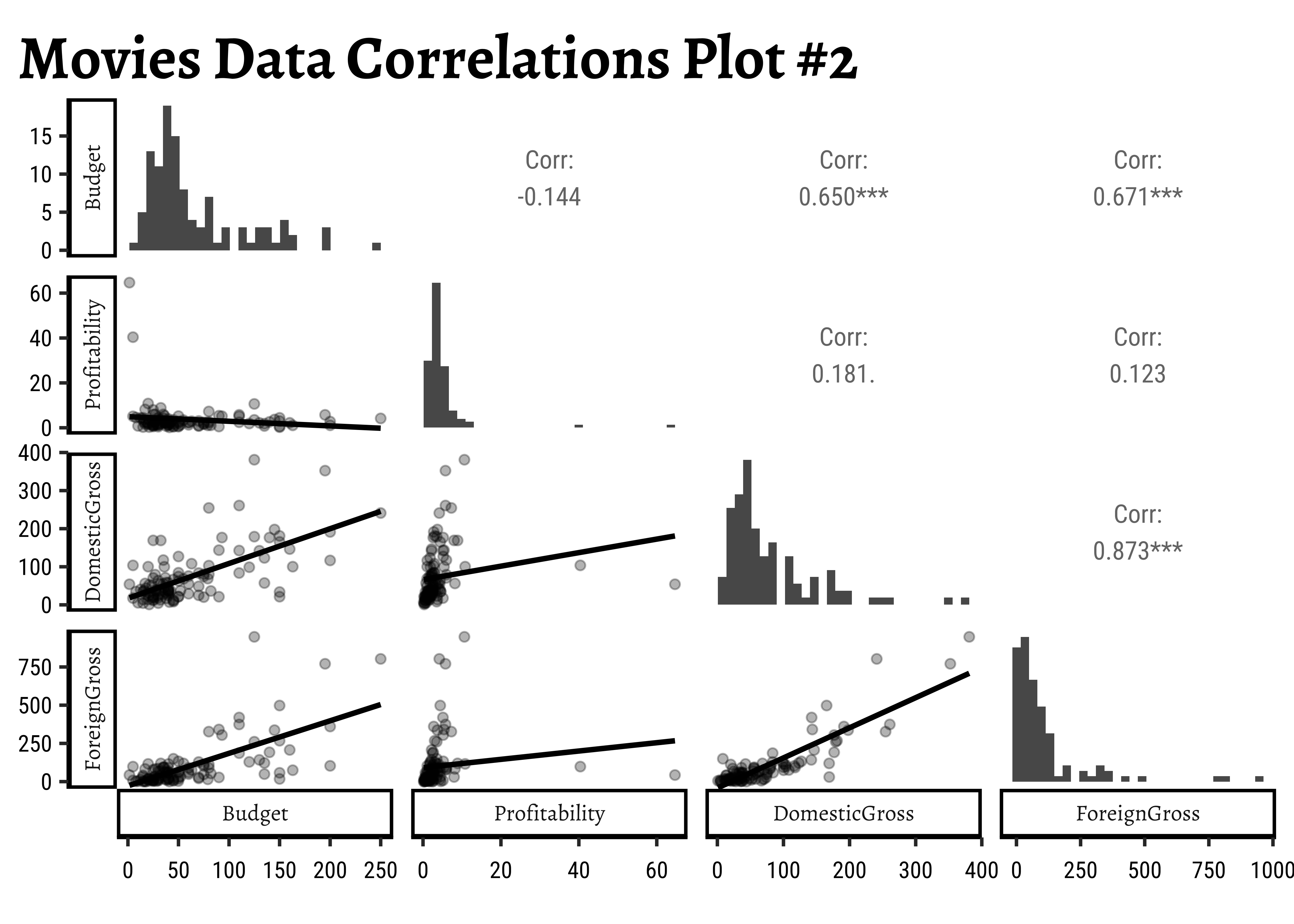
Let us also try a few other variables, related to budget and profits. For instance, it would be interesting to see the relationship between Budget and Profitability and even either of the “gross” earnings and Profitability.

GGally::ggpairs(
  movies %>% drop_na(),
  # Select Quant variables only for now
  columns = c(
    "Budget", "Profitability", "DomesticGross", "ForeignGross"
  ),
  switch = "both",
  # axis labels in more traditional locations(left and bottom)

  progress = FALSE,
  # no compute progress messages needed

  # Choose the diagonal graphs (always single variable! Think!)
  diag = list(continuous = "barDiag"),
  # choosing histogram,not density

  # Choose lower triangle graphs, two-variable graphs
  lower = list(continuous = wrap("smooth", alpha = 0.3, se = FALSE)),
  title = "Movies Data Correlations Plot #2"
)

Business Insight from Pairs Plot #2

The Budget variable has good correlation scores with DomesticGross and ForeignGross
Profitability and Budget seem to have a very slight negative correlation, but this does not appear to be significant.

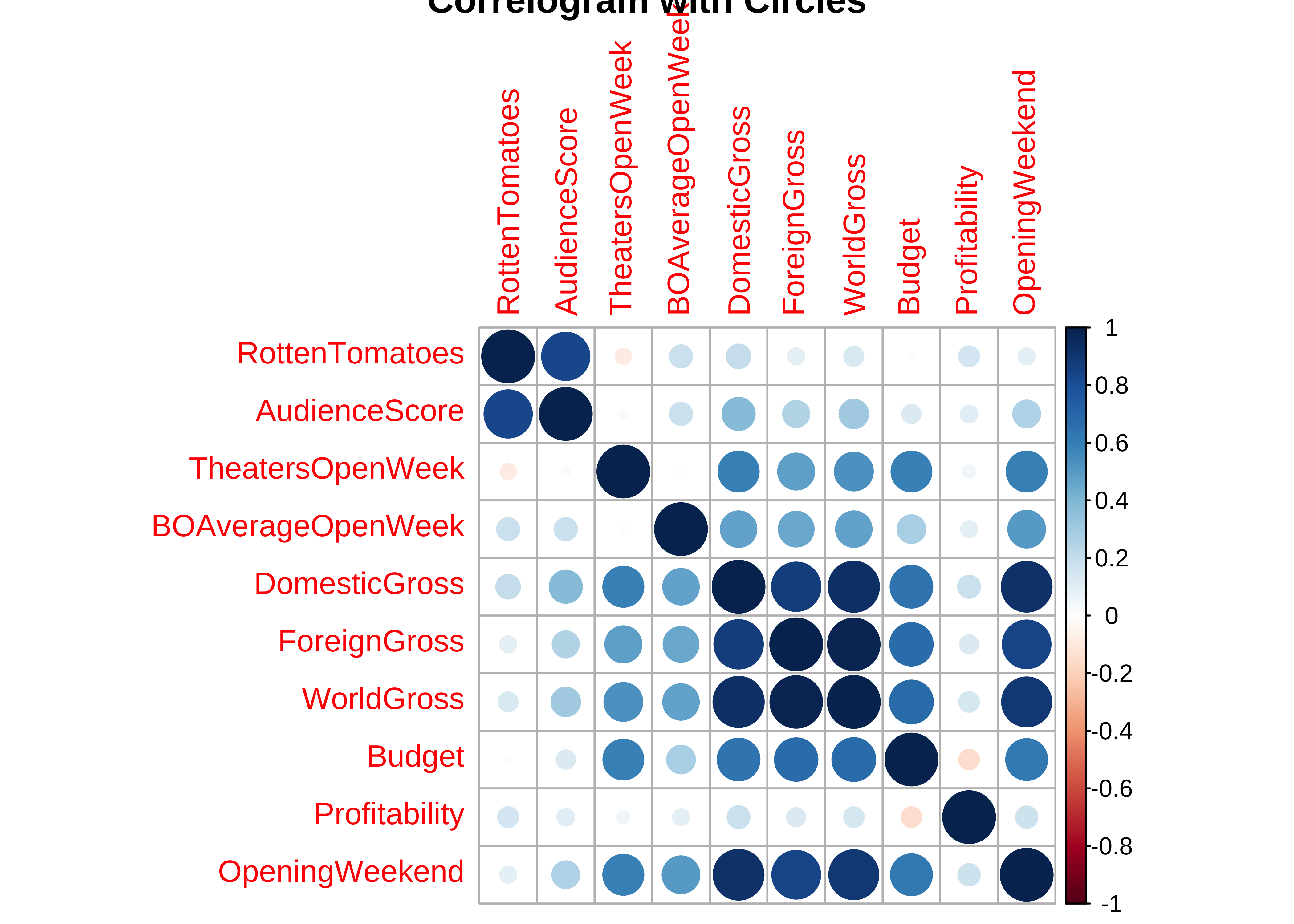
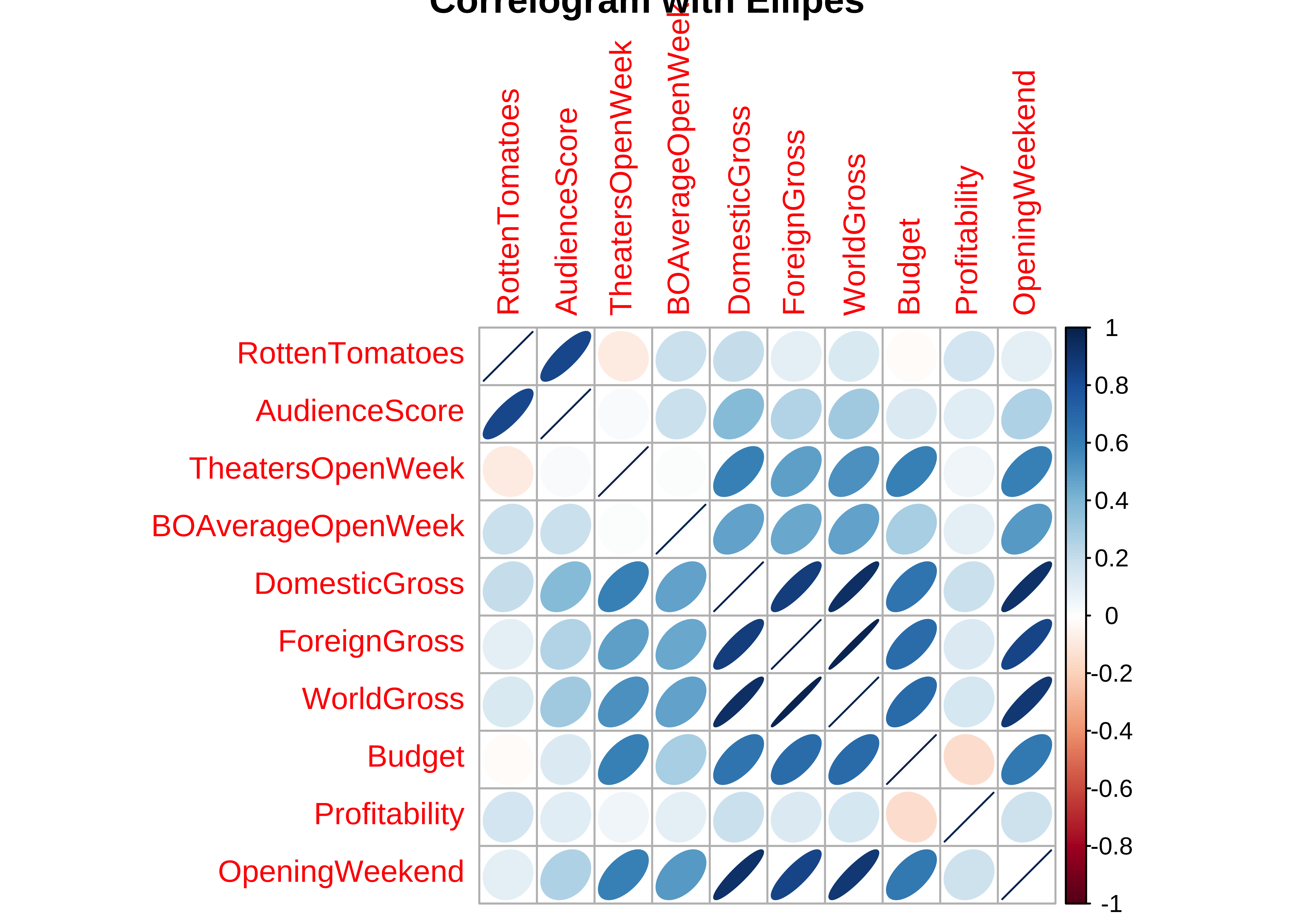
In this chart, the correlation between pairs of variables is shown symbolically as coloured shapes or colours. Circles, Squares, and Ellipse for example.

The size, colour, and “orientation” of the shapes in question symbolically represent the strength and polarity of the correlation scores.
The direction of the semi-major axis + the colour of the ellipse indicate whether the correlation score is positive or negative;
And the more eccentric the ellipse, the higher is the correlation score in value.

Note

Whereas GGally computes the correlation scores, corplot “merely” displays them in an evocative way. We need to compute the correlations a priori.

Note also:

Tip

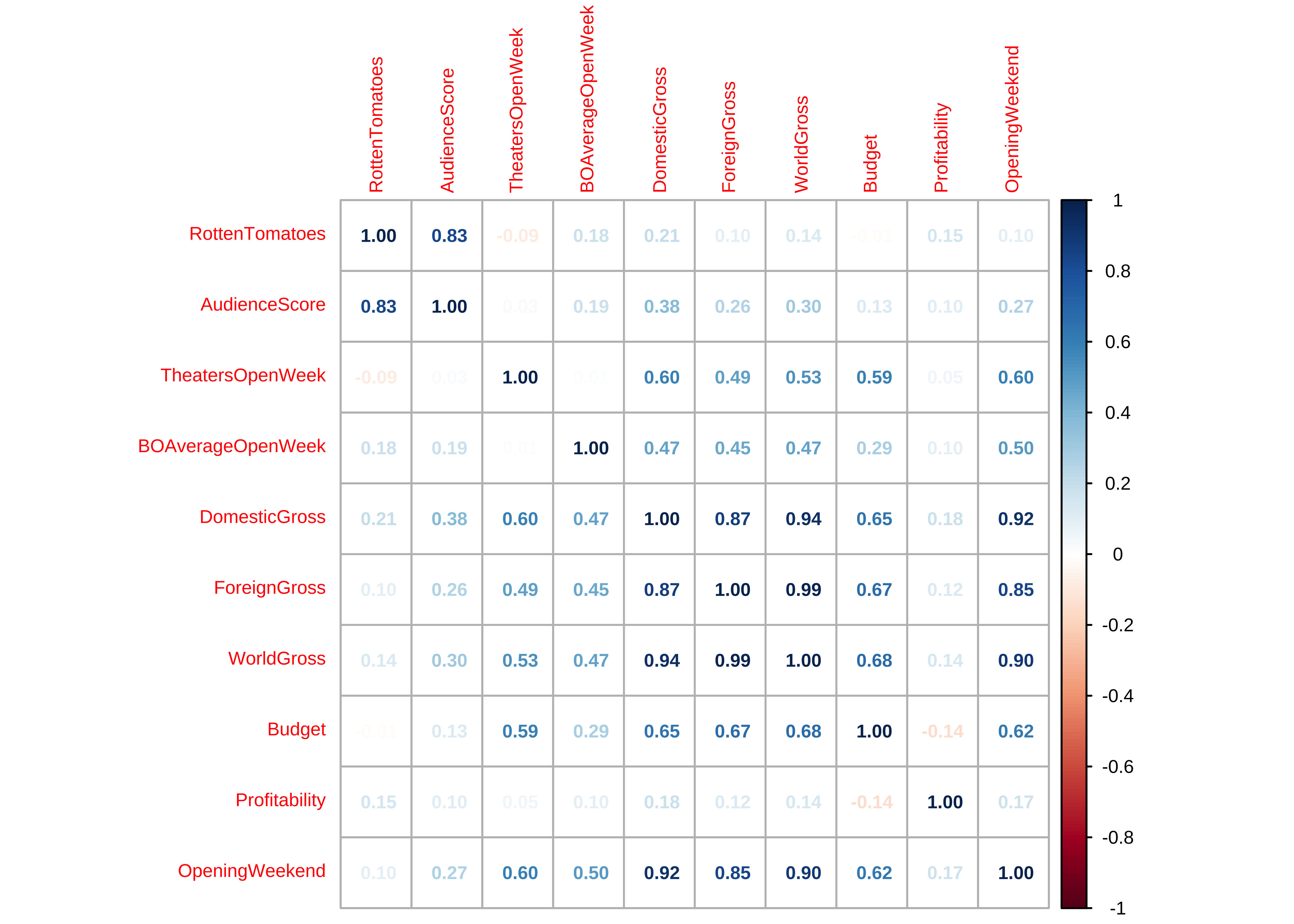
R package corrplot provides a visual exploratory tool on correlation matrix that supports automatic variable reordering to help detect hidden patterns among variables. corrplot is very easy to use and provides a rich array of plotting options in visualization method, graphic layout, color, legend, text labels, etc. It also provides p-values and confidence intervals to help users determine the statistical significance of the correlations.

# library(corrplot)
mydata_cor <- cor(movies_quant)
mydata_cor %>%
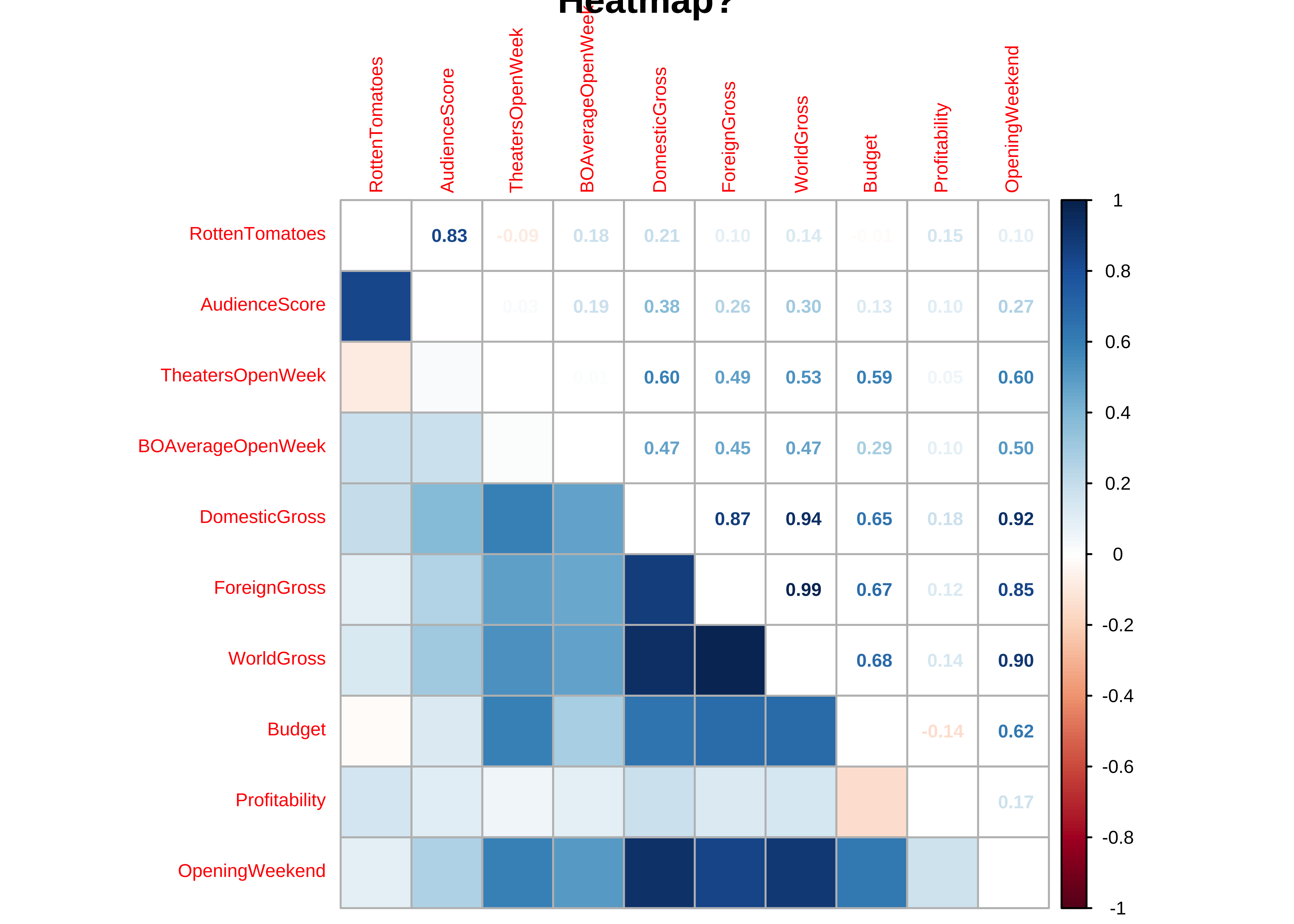
  knitr::kable(caption = "Correlation Scores Matrix")

Correlation Scores Matrix
	RottenTomatoes	AudienceScore	TheatersOpenWeek	BOAverageOpenWeek	DomesticGross	ForeignGross	WorldGross	Budget	Profitability	OpeningWeekend
RottenTomatoes	1.0000000	0.8329740	-0.0873543	0.1823480	0.2085935	0.0979132	0.1356232	-0.0147887	0.1502764	0.0986304
AudienceScore	0.8329740	1.0000000	0.0259118	0.1851768	0.3849406	0.2557891	0.3037927	0.1268649	0.1047582	0.2695132
TheatersOpenWeek	-0.0873543	0.0259118	1.0000000	0.0117674	0.5981162	0.4850569	0.5344582	0.5924941	0.0547807	0.5977724
BOAverageOpenWeek	0.1823480	0.1851768	0.0117674	1.0000000	0.4713164	0.4522253	0.4710352	0.2880262	0.0964176	0.5043684
DomesticGross	0.2085935	0.3849406	0.5981162	0.4713164	1.0000000	0.8725927	0.9374780	0.6497274	0.1812387	0.9232259
ForeignGross	0.0979132	0.2557891	0.4850569	0.4522253	0.8725927	1.0000000	0.9880383	0.6707613	0.1230330	0.8487202
WorldGross	0.1356232	0.3037927	0.5344582	0.4710352	0.9374780	0.9880383	1.0000000	0.6830783	0.1448857	0.8962294
Budget	-0.0147887	0.1268649	0.5924941	0.2880262	0.6497274	0.6707613	0.6830783	1.0000000	-0.1437862	0.6228180
Profitability	0.1502764	0.1047582	0.0547807	0.0964176	0.1812387	0.1230330	0.1448857	-0.1437862	1.0000000	0.1713962
OpeningWeekend	0.0986304	0.2695132	0.5977724	0.5043684	0.9232259	0.8487202	0.8962294	0.6228180	0.1713962	1.0000000

## View the matrix
corrplot::corrplot(mydata_cor,
  method = "number",
  number.cex = 0.6,
  cl.cex = 0.6, tl.cex = 0.6
)

# Default plot with circles
corrplot(mydata_cor,
  method = "circle",
  main = "Correlogram with Circles"
)

# Ellipse plot
corrplot(mydata_cor,
  method = "ellipse",
  main = "Correlogram with Ellipes"
)

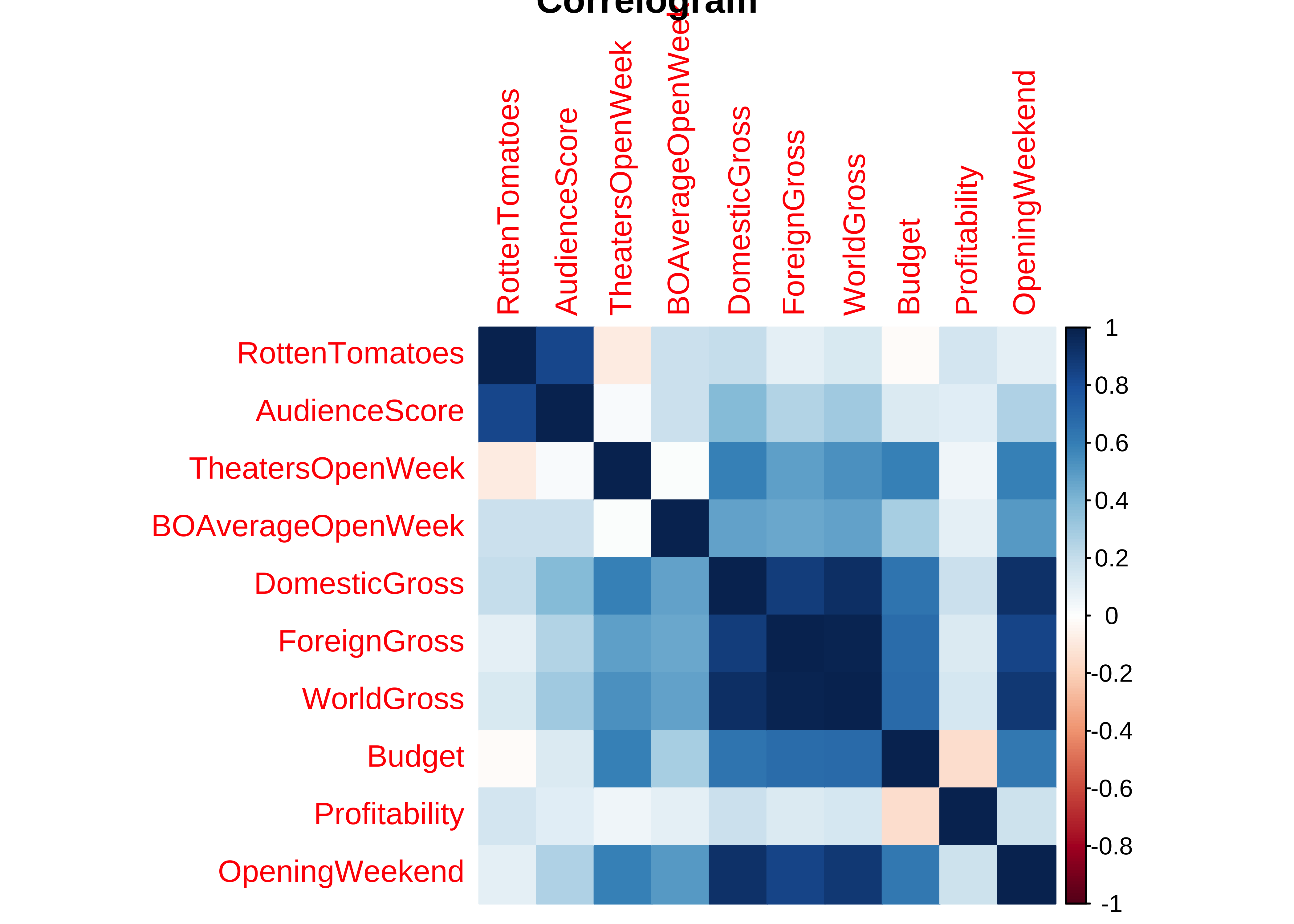
# Heatmap
corrplot(mydata_cor,
  method = "color", ## US Spelling only
  main = "Correlogram"
)

# Heatmap with numbers
corrplot.mixed(mydata_cor,
  lower = "color", number.cex = 0.6,
  cl.cex = 0.6, tl.cex = 0.6,
  upper = "number",
  tl.pos = "l",
  main = "Heatmap?"
)

Business Insights from corplots

Most of the variables here have positive correlations, many of them are significant

Doing a Correlation Test

Correlations scores can be obtained by conducting a formal test in R. We will use the mosaic function cor_test to get these results:

mosaic::cor_test(Profitability ~ Budget, data = movies) %>%
  broom::tidy() %>%
  knitr::kable(
    digits = 2,
    caption = "Movie Profitability vs Budget"
  )

Movie Profitability vs Budget
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
-0.08	-0.96	0.34	132	-0.25	0.09	Pearson’s product-moment correlation	two.sided

mosaic::cor_test(DomesticGross ~ Budget, data = movies) %>%
  broom::tidy() %>%
  knitr::kable(
    digits = 2,
    caption = "Movie Domestic Gross vs Budget"
  )

Movie Domestic Gross vs Budget
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.7	11.06	0	131	0.6	0.77	Pearson’s product-moment correlation	two.sided

mosaic::cor_test(ForeignGross ~ Budget, data = movies) %>%
  broom::tidy() %>%
  knitr::kable(
    digits = 2,
    caption = "Movie Foreign Gross vs Budget"
  )

Movie Foreign Gross vs Budget
estimate	statistic	p.value	parameter	conf.low	conf.high	method	alternative
0.69	10.22	0	118	0.58	0.77	Pearson’s product-moment correlation	two.sided

Business Insights from Correlation Tests

The budget and profitability are not well correlated, sadly. We see this from the p.value which is $0.34$ and the confidence values for the correlation estimate which also cover $0$ .

However, both DomesticGross and ForeignGross are well correlated with Budget. Look at the p.value (=0) and the confidence intervals which are unipolar.

The ErrorBar Plot for Correlations

As stated earlier, in our dataset we have a specific dependent or target variable, which represents the outcome of our experiment or our business situation. The remaining variables are usually independent or predictor variables. A very useful thing to know, and to view, would be the correlations of all independent variables. Using the correlation package from the easystats family of R packages, this can be very easily achieved. Let us quickly do this for the familiar mtcars dataset: we will quickly glimpse it, identify the target variable, and plot the correlations:

glimpse(mtcars)

Rows: 32
Columns: 11
$ mpg  <dbl> 21.0, 21.0, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19.2, 17.8,…
$ cyl  <dbl> 6, 6, 4, 6, 8, 6, 8, 4, 4, 6, 6, 8, 8, 8, 8, 8, 8, 4, 4, 4, 4, 8,…
$ disp <dbl> 160.0, 160.0, 108.0, 258.0, 360.0, 225.0, 360.0, 146.7, 140.8, 16…
$ hp   <dbl> 110, 110, 93, 110, 175, 105, 245, 62, 95, 123, 123, 180, 180, 180…
$ drat <dbl> 3.90, 3.90, 3.85, 3.08, 3.15, 2.76, 3.21, 3.69, 3.92, 3.92, 3.92,…
$ wt   <dbl> 2.620, 2.875, 2.320, 3.215, 3.440, 3.460, 3.570, 3.190, 3.150, 3.…
$ qsec <dbl> 16.46, 17.02, 18.61, 19.44, 17.02, 20.22, 15.84, 20.00, 22.90, 18…
$ vs   <dbl> 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0,…
$ am   <dbl> 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0,…
$ gear <dbl> 4, 4, 4, 3, 3, 3, 3, 4, 4, 4, 4, 3, 3, 3, 3, 3, 3, 4, 4, 4, 3, 3,…
$ carb <dbl> 4, 4, 1, 1, 2, 1, 4, 2, 2, 4, 4, 3, 3, 3, 4, 4, 4, 1, 2, 1, 1, 2,…

## Target variable: mpg
## Calculate all correlations
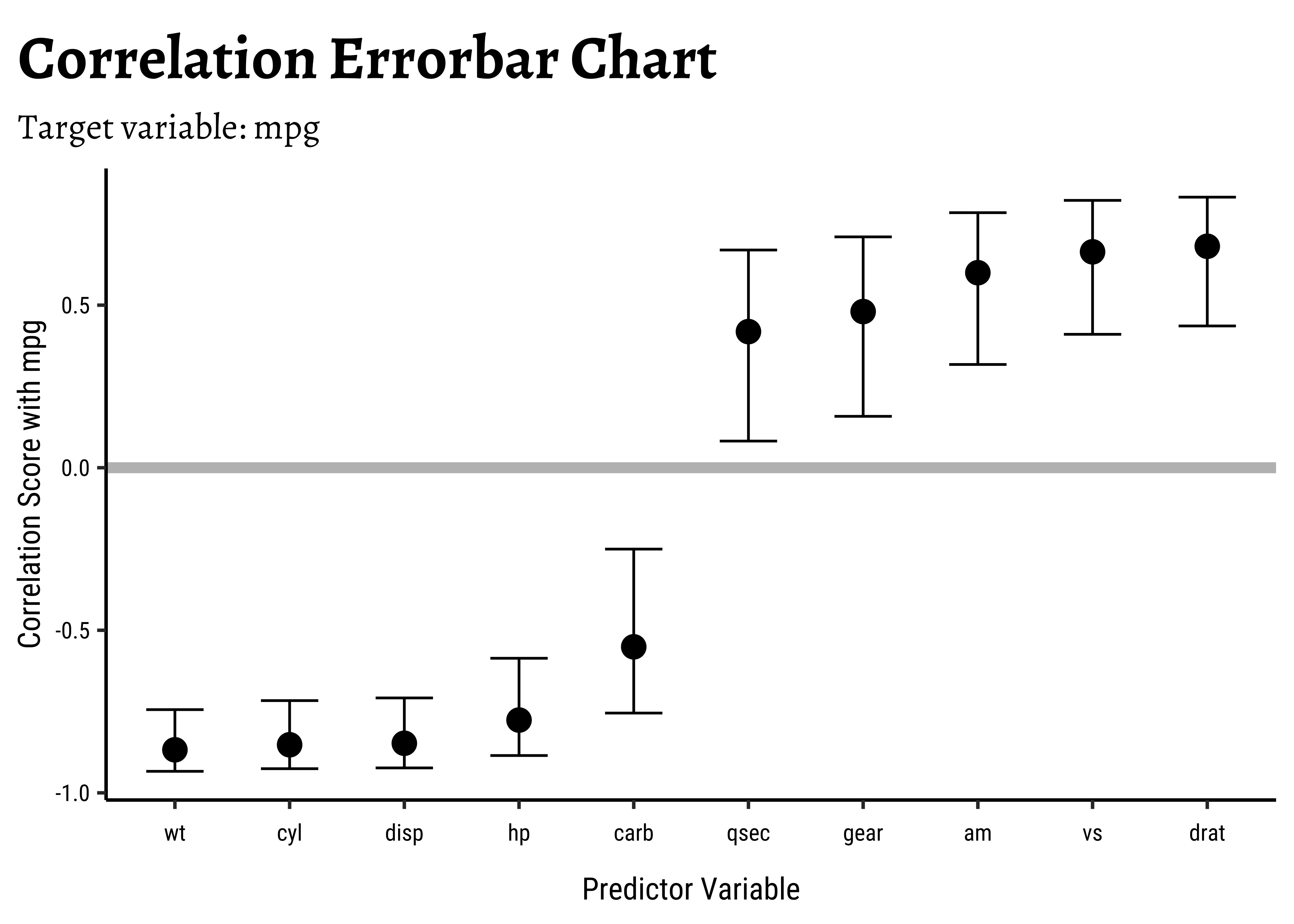
cor <- correlation::correlation(mtcars)
cor

ABCDEFGHIJ0123456789

	Parameter1 <chr>	Parameter2 <chr>	r <dbl>	CI <dbl>	CI_low <dbl>	CI_high <dbl>	t <dbl>	df_error <int>	p <dbl>
1	mpg	cyl	-0.85216196	0.95	-0.92576936	-0.7163171	-8.9196988	30	3.178597e-08
2	mpg	disp	-0.84755138	0.95	-0.92335937	-0.7081376	-8.7471515	30	4.783967e-08
3	mpg	hp	-0.77616837	0.95	-0.88526861	-0.5860994	-6.7423885	30	8.045259e-06
4	mpg	drat	0.68117191	0.95	0.43604838	0.8322010	5.0960421	30	5.861592e-04
5	mpg	wt	-0.86765938	0.95	-0.93382641	-0.7440872	-9.5590441	30	6.857981e-09
6	mpg	qsec	0.41868403	0.95	0.08195487	0.6696186	2.5252133	30	2.220659e-01
7	mpg	vs	0.66403892	0.95	0.41036301	0.8223262	4.8643850	30	1.093100e-03
8	mpg	am	0.59983243	0.95	0.31755830	0.7844520	4.1061270	30	8.265602e-03
9	mpg	gear	0.48028476	0.95	0.15806177	0.7100628	2.9991906	30	9.721707e-02
10	mpg	carb	-0.55092507	0.95	-0.75464796	-0.2503183	-3.6157497	30	2.385782e-02

We see correlation between all pairs of variables. We need to choose just those with target variable mpg:

cor %>%
  # Filter for target variable `mpg` and plot
  filter(Parameter1 == "mpg") %>%
  gf_point(r ~ reorder(Parameter2, r), size = 4) %>%
  gf_errorbar(CI_low + CI_high ~ reorder(Parameter2, r),
    width = 0.5
  ) %>%
  gf_hline(yintercept = 0, color = "grey", linewidth = 2) %>%
  gf_labs(
    title = "Correlation Errorbar Chart",
    subtitle = "Target variable: mpg",
    x = "Predictor Variable",
    y = "Correlation Score with mpg"
  )

Business Insights from ErrorBar Plot

Several variables are negatively correlated and some are positively correlated with ’mpg`. (The grey line shows “zero correlation”)
Since none of the error bars straddle zero, the correlations are mostly significant.

A New Combination Plot…

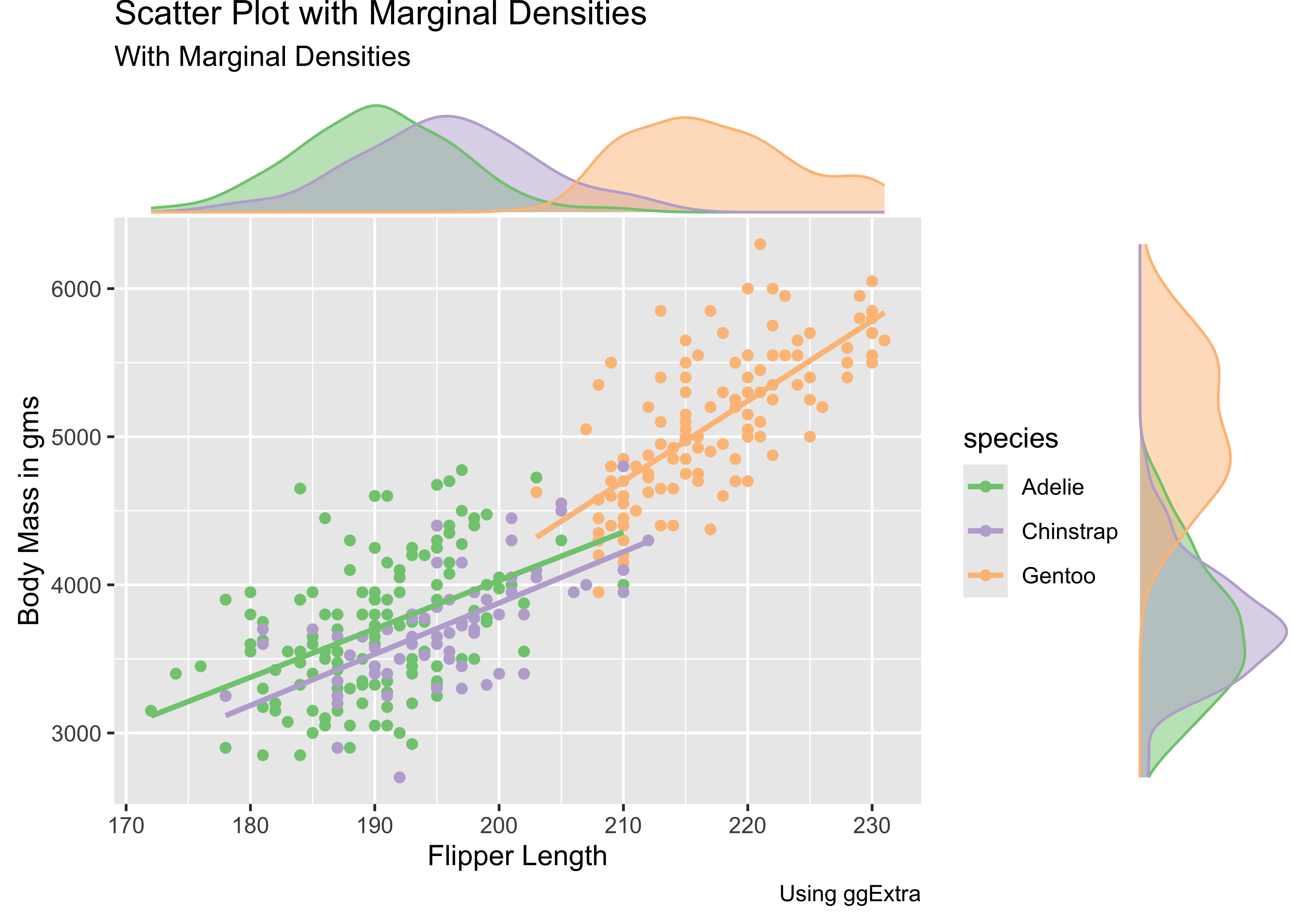
Sometimes, a simple scatter, or density alone, or viewed next to one another is not adequate to develop, or convey, our insight. We might just need a combination density + scatter plot. Such a plot can be be constructed from the ground up using ggformula or ggplot; however, there is a nice package called ggExtra that allows the creation of a powerful combination plot:

penguins %>%
  drop_na() %>%
  gf_point(body_mass_g ~ flipper_length_mm, colour = ~species) %>%
  gf_smooth(method = "lm") %>%
  gf_labs(x = "Flipper Length", y = "Body Mass in gms", title = "Penguins Scatter Plot", subtitle = "With Marginal Densities", caption = "Using ggExtra") %>%
  gf_refine(scale_colour_brewer(palette = "Accent")) %>%
  gf_labs(title = "Scatter Plot with Marginal Densities") %>%
  ggExtra::ggMarginal(
    type = "density", groupColour = TRUE,
    groupFill = TRUE, margins = "both"
  )

An Interactive Correlation Game

Head off to this interactive game website where you can play with correlations!

https://openintro.shinyapps.io/correlation_game/

Simpson’s Paradox

See how the overall correlation/regression line slopes upward, whereas that for the individual groups slopes downward!! This is an example of Simpson’s Paradox!

Your Turn

Try to play this online Correlation Game.

2. School Expenditure and Grades.

3. Gas Prices and Consumption

As described here. Note the log-transformed Quant data…why do you reckon this was done in the data set itself?

4. Horror Movies (Bah.You awful people..)

6. Food Delivery Times

Wait, But Why?

Scatter Plots, when they show “linear” clouds, tell us that there is some relationship between two Quant variables we have just plotted
If so, then if one is the target variable you are trying to design for, then the other independent, or controllable, variable is something you might want to design with.

Important

Target variables are usually plotted on the Y-axis, while Predictor variables are on the X-Axis, in a Scatter Plot. Why? Because $y = m x + c$ !

Correlation scores are good indicators of things that are, well, related. While one variable may not necessarily cause another, a good correlation score may indicate how to chose a good predictor.
That is something we will see when we examine Linear Regression
Always, always, plot and test your data! Both numerical summaries as tables, and graphical summaries as charts, are necessary! See below!!

And How about these datasets?

dataset	mean_x	mean_y	std_dev_x	std_dev_y	corr_x_y
away	54.26610	47.83472	16.76982	26.93974	-0.06412835
bullseye	54.26873	47.83082	16.76924	26.93573	-0.06858639
circle	54.26732	47.83772	16.76001	26.93004	-0.06834336
dino	54.26327	47.83225	16.76514	26.93540	-0.06447185
dots	54.26030	47.83983	16.76774	26.93019	-0.06034144
h_lines	54.26144	47.83025	16.76590	26.93988	-0.06171484
high_lines	54.26881	47.83545	16.76670	26.94000	-0.06850422
slant_down	54.26785	47.83590	16.76676	26.93610	-0.06897974
slant_up	54.26588	47.83150	16.76885	26.93861	-0.06860921
star	54.26734	47.83955	16.76896	26.93027	-0.06296110
v_lines	54.26993	47.83699	16.76996	26.93768	-0.06944557
wide_lines	54.26692	47.83160	16.77000	26.93790	-0.06657523
x_shape	54.26015	47.83972	16.76996	26.93000	-0.06558334

Yes, you did want to plot that cute T-Rex, didn’t you? Here is the data then!!

Warning

Can selling more ice-cream make people drown?
Use your head about pairs of variables. Do not fall into this trap)

Conclusions

Scatter Plots give a us sense of change; whether it is linear or non-linear. We can get an idea of correlation between variables with a scatter plot. Our workflow for evaluating correlations between target variable and several other predictor variables uses several packages such as GGally, corrplot, correlation, and of course mosaic for correlation tests.

AI Generated Summary and Podcast

This document focusses on correlation between quantitative variables. It examines different ways to visualize correlations, including scatter plots and correlograms. The document provides examples of how to use R packages like GGally and corrplot to create these visualizations and correlation tests to assess the strength and significance of relationships between variables. The tutorial uses the HollywoodMovies2011 and mtcars datasets as examples to demonstrate these concepts.

References

Winston Chang (2024). R Graphics Cookbook. https://r-graphics.org
Minimal R using mosaic. https://cran.r-project.org/web/packages/mosaic/vignettes/MinimalRgg.pdf
Antoine Soetewey. Pearson, Spearman and Kendall correlation coefficients by hand https://www.r-bloggers.com/2023/09/pearson-spearman-and-kendall-correlation-coefficients-by-hand/
Taiyun Wei, Viliam Simko. An Introduction to corrplot Package. https://cran.r-project.org/web/packages/corrplot/vignettes/corrplot-intro.html

R Package Citations

Package	Version	Citation
corrplot	0.95	Wei and Simko (2024)
datasauRus	0.1.9	Gillespie et al. (2025)
GGally	2.2.1	Schloerke et al. (2024)
ggExtra	0.10.1	Attali and Baker (2023)
latex2exp	0.9.6	Meschiari (2022)

Attali, Dean, and Christopher Baker. 2023. ggExtra: Add Marginal Histograms to “ggplot2,” and More “ggplot2” Enhancements. https://doi.org/10.32614/CRAN.package.ggExtra.

Gillespie, Colin, Steph Locke, Rhian Davies, and Lucy D’Agostino McGowan. 2025. datasauRus: Datasets from the Datasaurus Dozen. https://doi.org/10.32614/CRAN.package.datasauRus.

Meschiari, Stefano. 2022. Latex2exp: Use LaTeX Expressions in Plots. https://doi.org/10.32614/CRAN.package.latex2exp.

Schloerke, Barret, Di Cook, Joseph Larmarange, Francois Briatte, Moritz Marbach, Edwin Thoen, Amos Elberg, and Jason Crowley. 2024. GGally: Extension to “ggplot2”. https://doi.org/10.32614/CRAN.package.GGally.

Wei, Taiyun, and Viliam Simko. 2024. R Package “corrplot”: Visualization of a Correlation Matrix. https://github.com/taiyun/corrplot.

Citation

BibTeX citation:

@online{v.2022,
  author = {V., Arvind},
  title = {\textless Iconify-Icon Icon=“icon-Park-Outline:change”
    Width=“1.2em”
    Height=“1.2em”\textgreater\textless/Iconify-Icon\textgreater{}
    {Change}},
  date = {2022-11-22},
  url = {https://av-quarto.netlify.app/content/courses/Analytics/Descriptive/Modules/30-Correlations/},
  langid = {en},
  abstract = {How one variable changes with another}
}

For attribution, please cite this work as:

V., Arvind. 2022. “<Iconify-Icon Icon=‘icon-Park-Outline:change’ Width=‘1.2em’ Height=‘1.2em’></Iconify-Icon> Change.” November 22, 2022. https://av-quarto.netlify.app/content/courses/Analytics/Descriptive/Modules/30-Correlations/.

Slides and Tutorials

Setting up R Packages

Plot Fonts and Theme

What graphs will we see today?

What kind of Data Variables will we choose?

Inspiration

What is Correlation?

Pearson Correlation coefficient

Case Study-1: HollywoodMovies2011 dataset

Inspecting the Data

Scatter Plots

Quantizing Correlation

Doing a Correlation Test

The ErrorBar Plot for Correlations

A New Combination Plot…

An Interactive Correlation Game

Simpson’s Paradox

Your Turn

Wait, But Why?

Conclusions

AI Generated Summary and Podcast

References

R Package Citations

Citation

Case Study-1: `HollywoodMovies2011` dataset